Pervoobraznaya.ppt

Содержание
Определение первообразной
Основное свойство первообразной
Три правила нахождения первообразных

Определение первообразной
Функция F называется первообразной для функции f на заданном промежутке, если для всех x из этого промежутка
F′(x) = f(x)
F(x) = x3/3 есть первообразная для функции f(x)=x2 на интервале (-∞; ∞), так как
F′(x) = (x3/3)′ = 1/3(x3)′ = 1/3*3x2 = x2 = f(x)
для всех x ∈ (-∞; ∞).
Пример:

Основное свойство первообразной
Любая первообразная для функции f на промежутке I может быть записана в виде
F(x) + C,
Где F(x) – одна из первообразных для функции f(x) на промежутке I, а С – произвольная постоянная.
Признак постоянства функции
Если F′(x) = 0 на некотором промежутке I, то функция F – постоянная на этом промежутке.

Свойства:
Какое бы число не подставить в формулу С получим первообразную для функции f на промежутке I.
Какую бы первообразную F для f на промежутке I не взять, можно подобрать такое чисто С, что для всех значений x из промежутка I выполнится равенство
Φ (x) = F(x) + C
График двух любых первообразных для функции получается путем параллельного переноса вдоль оси OY.

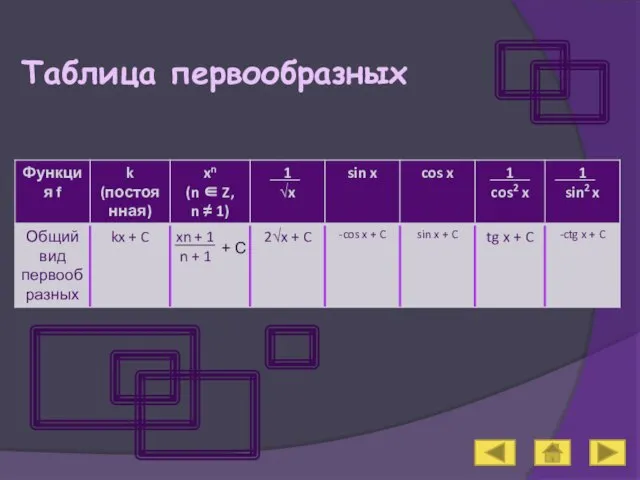
Таблица первообразных

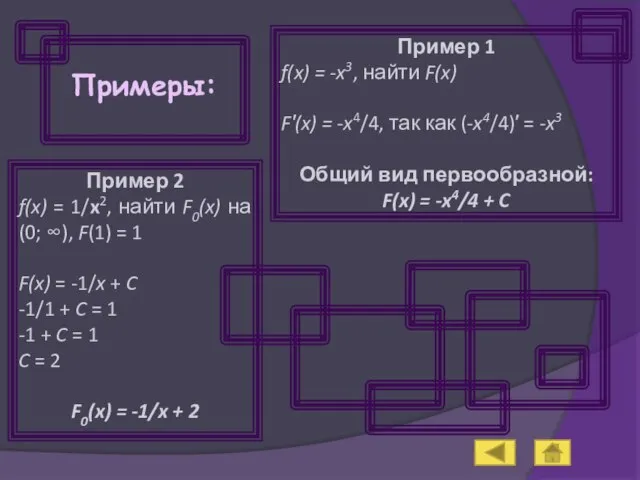
Примеры:
Пример 1
f(x) = -x3, найти F(x)
F′(x) = -x4/4, так как (-x4/4)′ = -x3
Общий вид первообразной:
F(x) = -x4/4 + C
Пример 2
f(x) = 1/x2, найти F0(x) на (0; ∞), F(1) = 1
F(x) = -1/x + C
-1/1 + C = 1
-1 + C = 1
C = 2
F0(x) = -1/x + 2

Три правила нахождения первообразных
Правило 1
Если F есть первообразная для f, а G – первообразная для g, то F + G есть первообразная для f + g:
(F + G)′ = F ′ + G ′ = f + g
Пример
f(x) = x3 + 1/x2, найти F(x)
(x3)′ = x4/4
(1/x2)′ = -1/x, =>
F(x) = x4/4 - 1/x + C

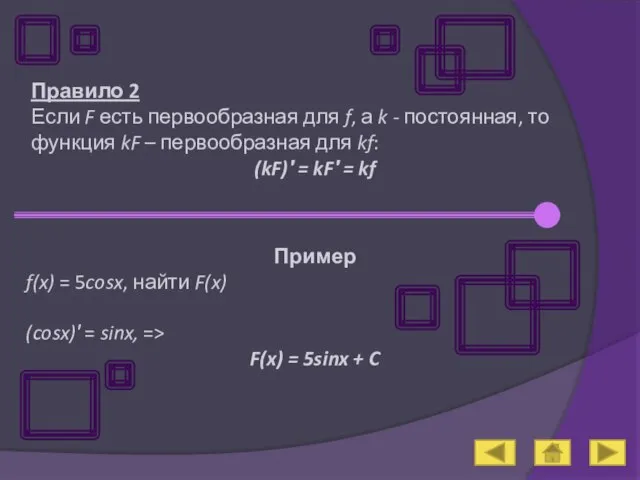
Правило 2
Если F есть первообразная для f, а k - постоянная, то функция kF – первообразная для kf:
(kF)′ = kF′ = kf
Пример
f(x) = 5cosx, найти F(x)
(cosx)′ = sinx, =>
F(x) = 5sinx + C