Содержание
- 2. Вариант 1 Самостоятельная работа x³ y = e y = ln (x² +1) Построить график функции
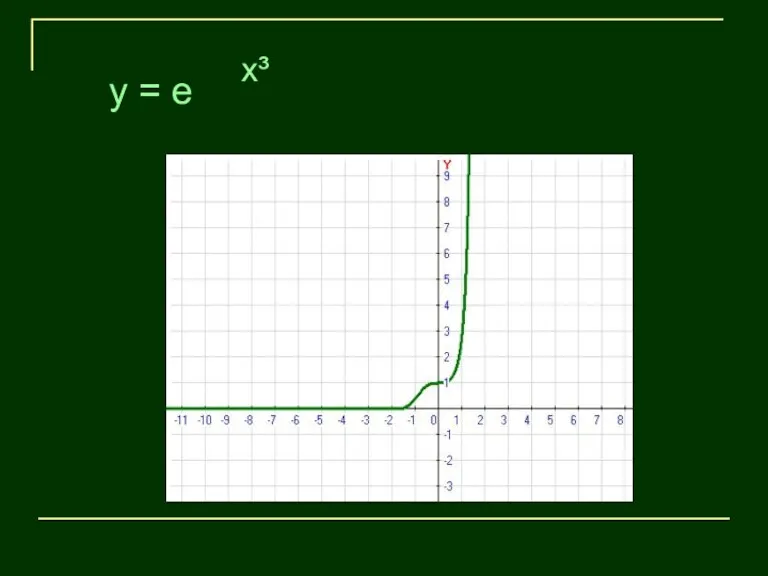
- 3. x³ y = e
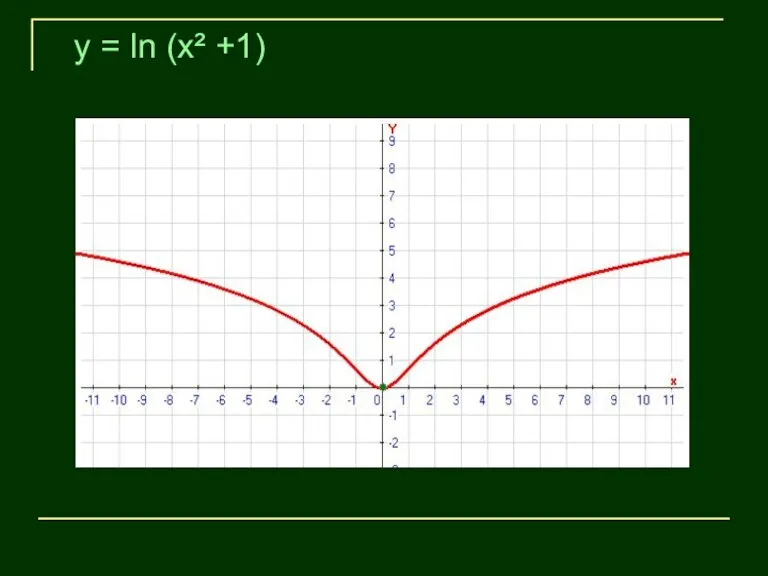
- 4. y = ln (x² +1)
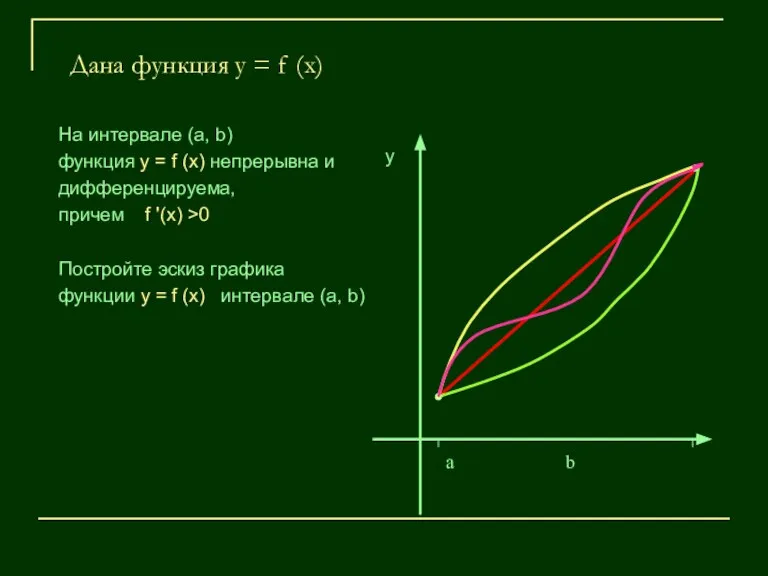
- 5. Дана функция у = f (x) На интервале (а, b) функция у = f (x) непрерывна
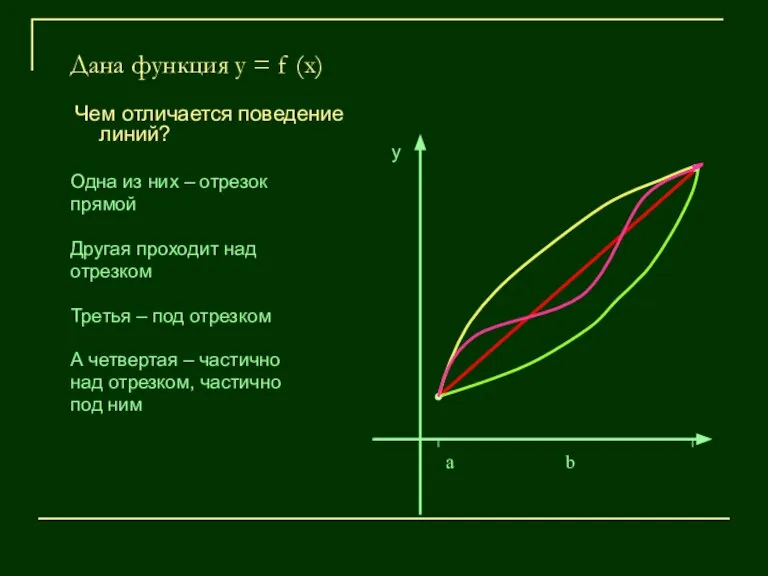
- 6. Дана функция у = f (x) Чем отличается поведение линий? Одна из них – отрезок прямой
- 7. В математике для обозначения такого поведения существуют специальные понятия: выпуклости и вогнутости графика функции
- 8. Выпуклость и вогнутость функции Геометрический смысл второй производной
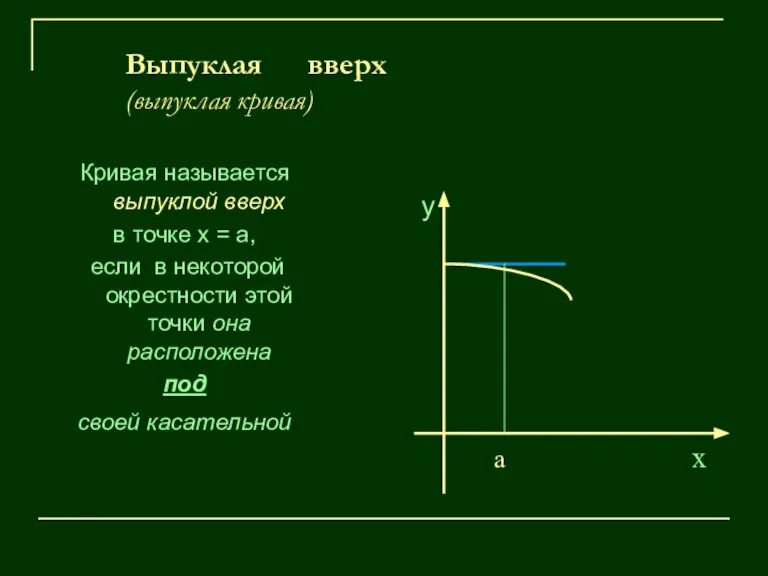
- 9. Выпуклая вверх (выпуклая кривая) Кривая называется выпуклой вверх в точке х = а, если в некоторой
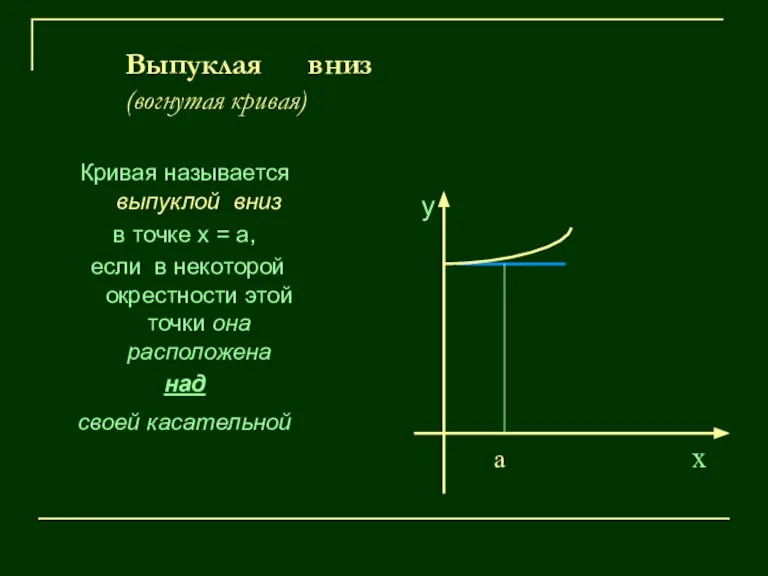
- 10. Выпуклая вниз (вогнутая кривая) Кривая называется выпуклой вниз в точке х = а, если в некоторой
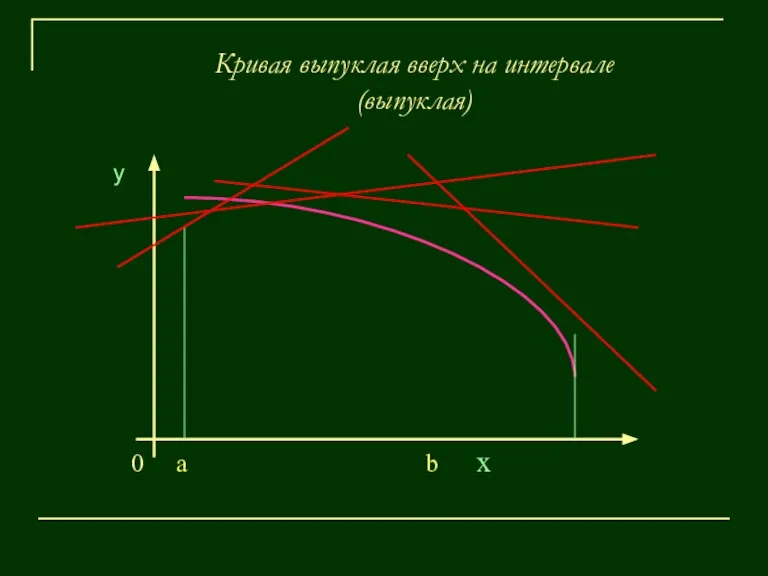
- 11. Кривая выпуклая вверх на интервале (выпуклая) у 0 a b х
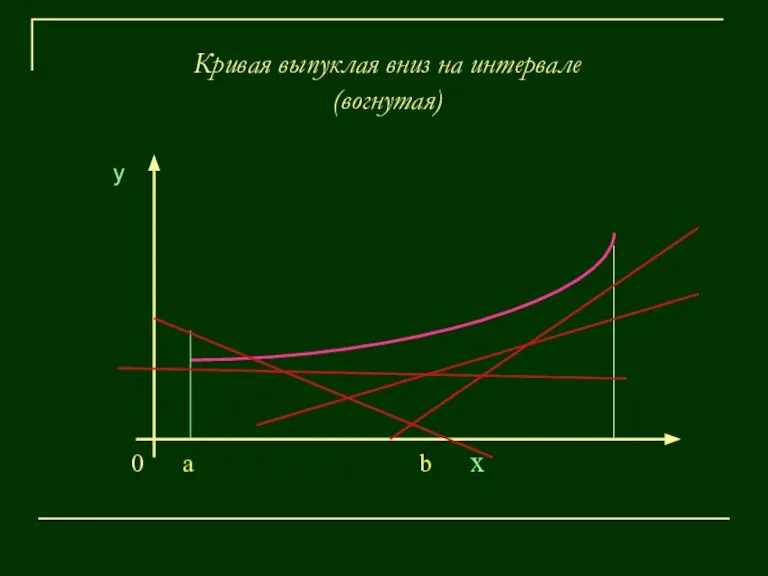
- 12. Кривая выпуклая вниз на интервале (вогнутая) у 0 a b х
- 13. Как найти интервалы выпуклости и вогнутости?
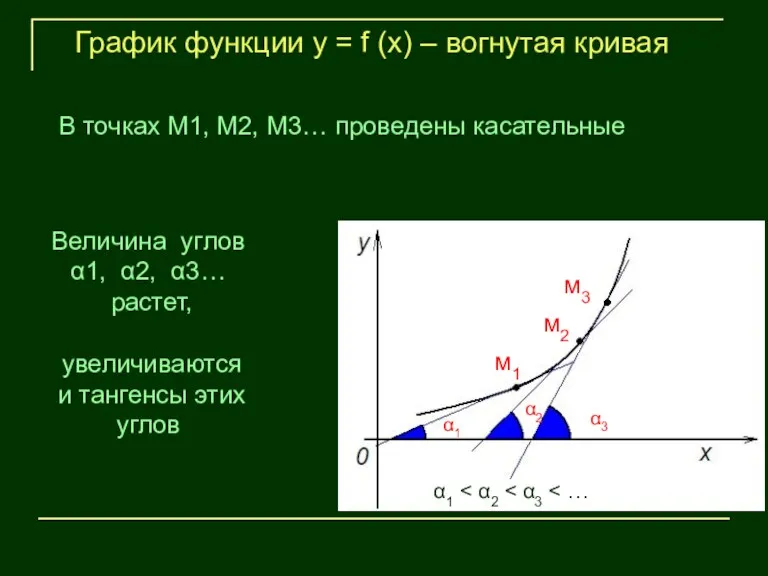
- 14. м1 м2 м3 α1 α2 α3 График функции у = f (х) – вогнутая кривая Величина
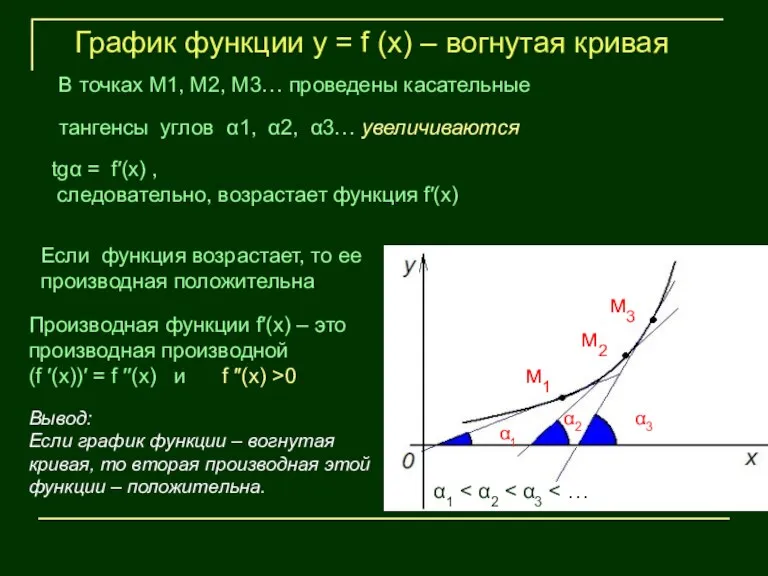
- 15. м1 м2 м3 α1 α2 α3 График функции у = f (х) – вогнутая кривая В
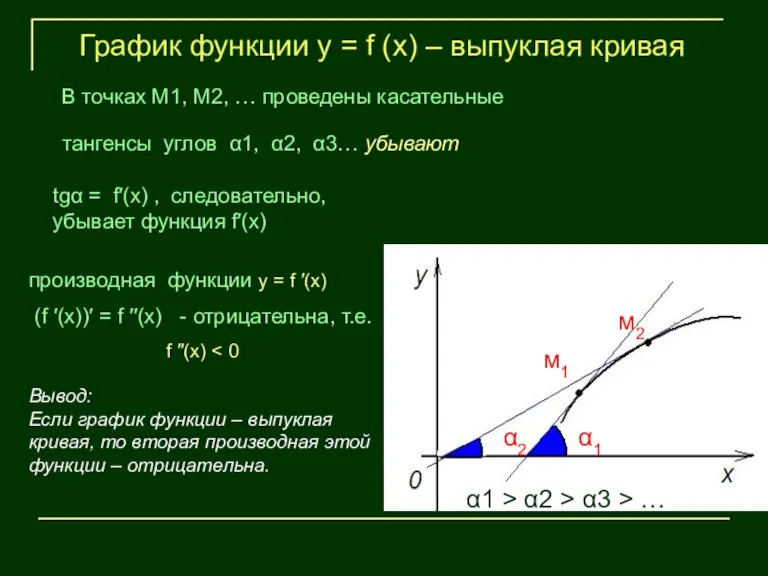
- 16. α1 График функции у = f (х) – выпуклая кривая tgα = f′(х) , следовательно, убывает
- 17. Если вторая производная функции у = f (х) на данном интервале положительна, то кривая вогнута а
- 18. Точки, в которых выпуклость меняется на вогнутость или наоборот, называются точками перегиба
- 19. Правило нахождения интервалов выпуклости и вогнутости графика функции: Найти: Вторую производную Точки, в которых она равна
- 20. Исследование функции с помощью второй производной Интервалы выпуклости: (-3, 0) и (2, 5) Интервалы вогнутости: (-∞,
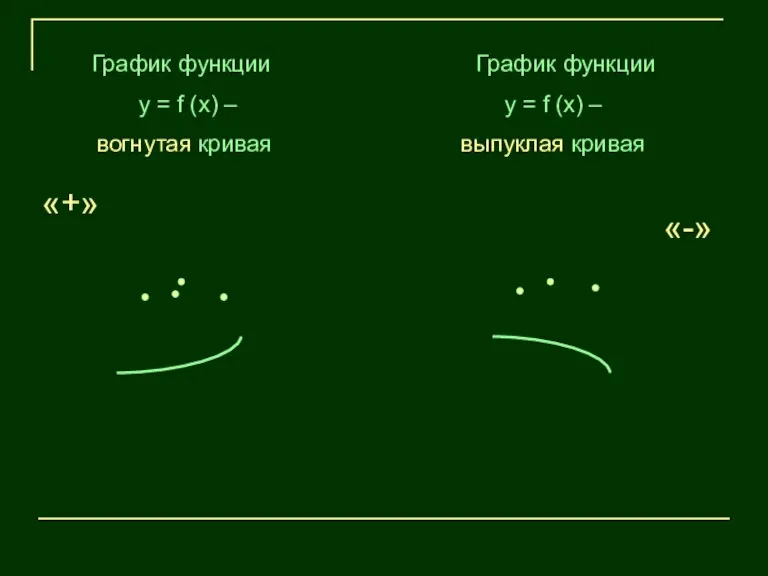
- 21. График функции у = f (х) – вогнутая кривая График функции у = f (х) –
- 22. Найти интервалы выпуклости и вогнутости и точки перегиба Вариант 1 у = х³ - 12х +
- 23. Проверка Вариант 1 у = х³ - 12х + 4 х – любое число f'(х) =
- 24. Проверка Вариант 2 у = ¼ х4 – 3/2 х² х – любое число f'(х) =
- 26. Скачать презентацию











 Формулы приведения
Формулы приведения Сумма «n» членов Арифметической прогрессии - презентация по Алгебре_
Сумма «n» членов Арифметической прогрессии - презентация по Алгебре_ Квадратные уравнения, способы их решения
Квадратные уравнения, способы их решения Теорема Виета (8 класс)
Теорема Виета (8 класс) Полиномы Одночлены Двучлены Трёхчлены Многочлены
Полиномы Одночлены Двучлены Трёхчлены Многочлены  «Применение производной для исследования функции»
«Применение производной для исследования функции»  Презентация на тему ТК РФ как источник трудового права РФ
Презентация на тему ТК РФ как источник трудового права РФ  Презентация по математике на тему: «Метод математической индукции»
Презентация по математике на тему: «Метод математической индукции»  Тізімдер мен кестелер
Тізімдер мен кестелер Презентация на тему Основные отечественные концепции управления качеством
Презентация на тему Основные отечественные концепции управления качеством  Презентация на тему Аварии на гидротехнических сооружениях
Презентация на тему Аварии на гидротехнических сооружениях  Виды показательных уравнений
Виды показательных уравнений  Уравнение и его корни 7 класс
Уравнение и его корни 7 класс ФОРМУЛЫ ПРИВЕДЕНИЯ Преподаватель ФГОУ СПО «СТК» Л.Г.Якимчук
ФОРМУЛЫ ПРИВЕДЕНИЯ Преподаватель ФГОУ СПО «СТК» Л.Г.Якимчук  Презентация на тему Достопримечательности Египта
Презентация на тему Достопримечательности Египта  Сложение и вычитание чисел с разными знаками
Сложение и вычитание чисел с разными знаками Презентация на тему Содержание экономической безопасности РФ
Презентация на тему Содержание экономической безопасности РФ  Арифметическая и геометрическая прогрессии
Арифметическая и геометрическая прогрессии Презентация на тему Система высшего образования в Японии
Презентация на тему Система высшего образования в Японии  Презентация на тему Основные закономерности развития науки
Презентация на тему Основные закономерности развития науки  Квадратичная функция
Квадратичная функция  Расположение точек относительно осей координат
Расположение точек относительно осей координат Обобщающий урок по теме: «Решение неравенств с одной переменной и решение систем неравенств»
Обобщающий урок по теме: «Решение неравенств с одной переменной и решение систем неравенств» Удивительные квадратные уравнения
Удивительные квадратные уравнения Пересечение и объединение множеств (8 класс)
Пересечение и объединение множеств (8 класс) Квадратичная функция 9 класс
Квадратичная функция 9 класс Умножение одночленов 7 класс
Умножение одночленов 7 класс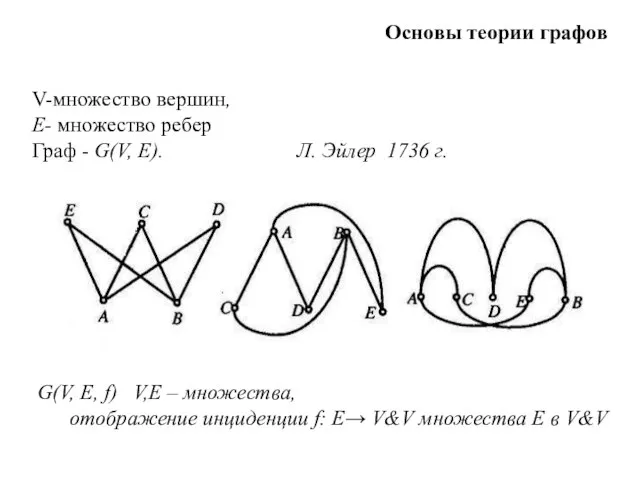 Основы теории графов
Основы теории графов