Преобразование графиков функций

Содержание
Параллельный перенос вдоль оси Параллельный перенос вдоль оси OY
Параллельный перенос вдоль оси ОХ
Растяжение (сжатие) в Растяжение (сжатие) в k Растяжение (сжатие) в k раз вдоль оси Растяжение (сжатие) в k раз вдоль оси OY
Растяжение (сжатие) в Растяжение (сжатие) в k Растяжение (сжатие) в k раз вдоль оси Растяжение (сжатие) в k раз вдоль оси OРастяжение (сжатие) в k раз вдоль оси OХ
Симметричное отображение относительно Симметричное отображение относительно Симметричное отображение относительно оси Симметричное отображение относительно оси OY
Симметричное отображение относительно Симметричное отображение относительно Симметричное отображение относительно оси Симметричное отображение относительно оси OX
Построение графика y=|f(x)|
Построение графика y=f(|x|)

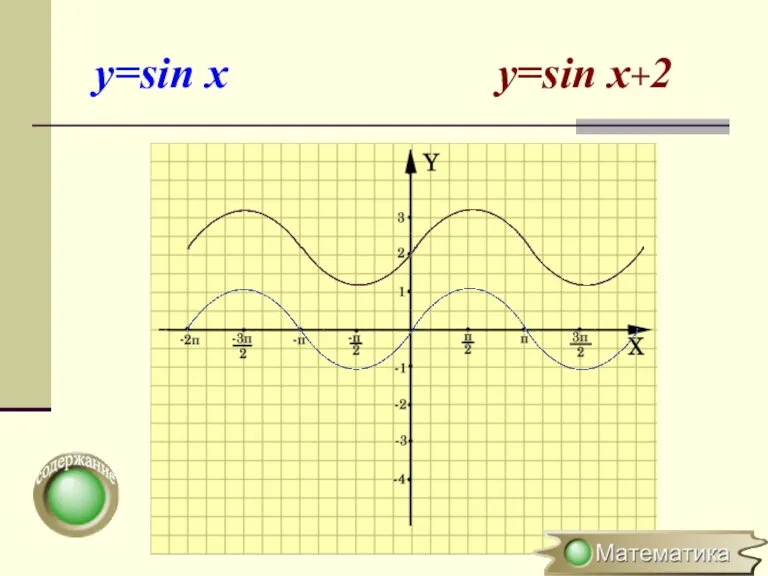
Параллельный перенос вдоль оси OY
y=f(x) → y=f(x)+a
(x0;y0) → (x0;y0+a) Для построения графика функции y=f(x)+a необходимо график функции y=f(x) перенести вдоль оси OY на вектор (0;а)

y=sin x y=sin x+2

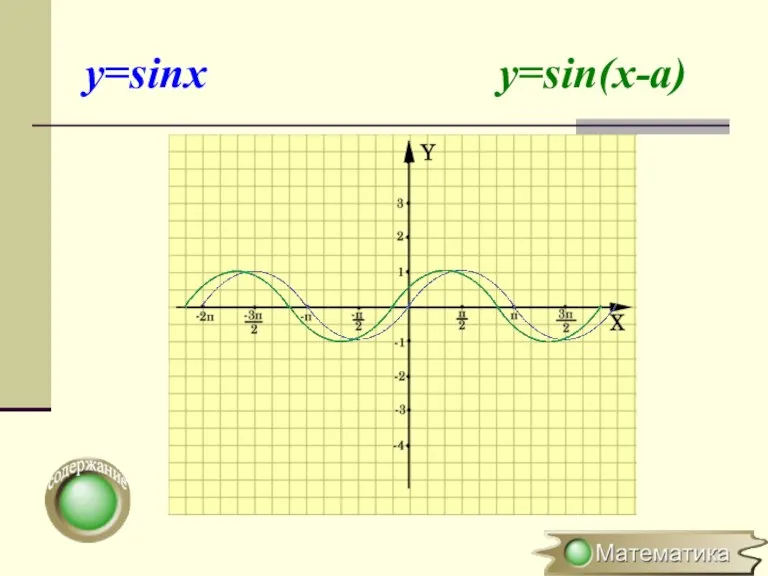
Параллельный перенос вдоль оси ОХ
y=f(x) → y=f(x-a)
(x0;y0) → (x0+a;y0) Для построения графика функции y=f(x-a) необходимо график функции y=f(x) перенести вдоль оси OX на вектор (0;а)

y=sinx y=sin(x-a)

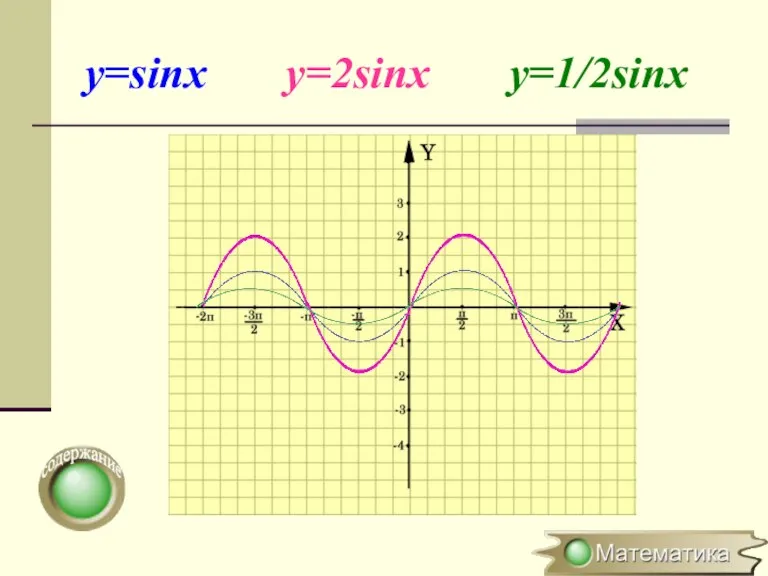
Растяжение (сжатие) в k раз вдоль оси OY
y=f(x) → y=kf(x), где k>0
(x0;y0) → (x0;ky0)
Для построения графика функции y=kf(x) необходимо график функции y=f(x) растянуть в k раз вдоль оси ОY для k >1 или сжать в 1/k развдоль оси OY для k<1

y=sinx y=2sinx y=1/2sinx

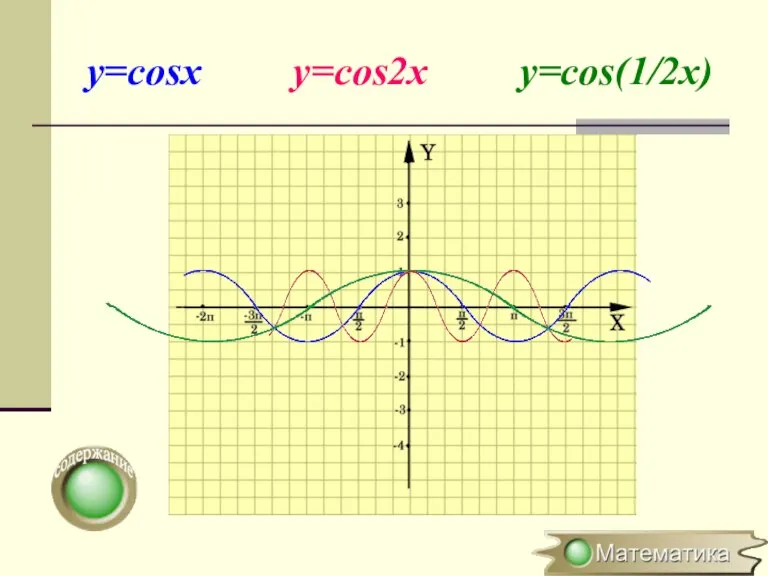
Растяжение (сжатие) в k раз вдоль оси OХ
y=f(x) → y=f(kx), где k>0
(x0;y0) → ( x0;y0)
Для построения графика функции y=f(kx) необходимо график функции y=f(x) сжать в k раз вдоль оси ОХ для k >1 или растянуть в 1/k раз вдоль оси OХ для k<1

y=cosx y=cos2x y=cos(1/2x)

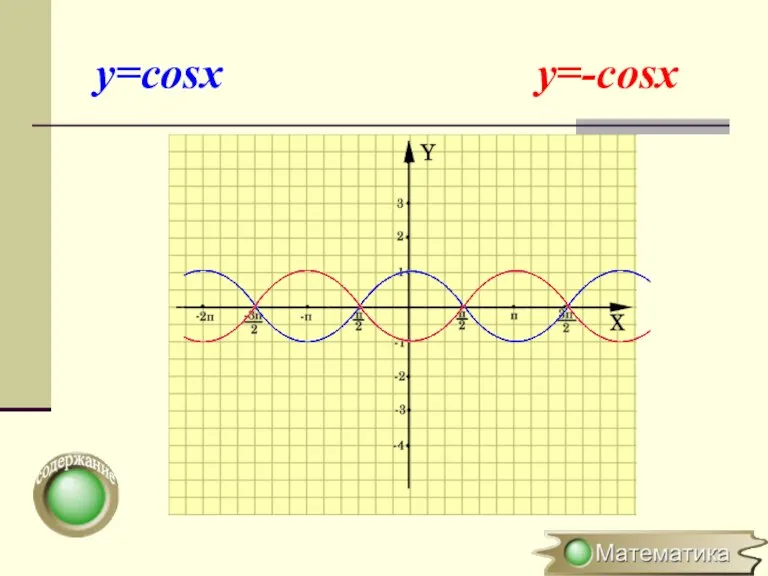
Симметричное отображение относительно оси OY
y=f(x) → y=-f(x)
(x0;y0) → (x0;-y0)
Для построения графика функции y=-f(x) необходимо график функции y=f(x)симметрично отобразить относительно оси ОХ

y=cosx y=-cosx

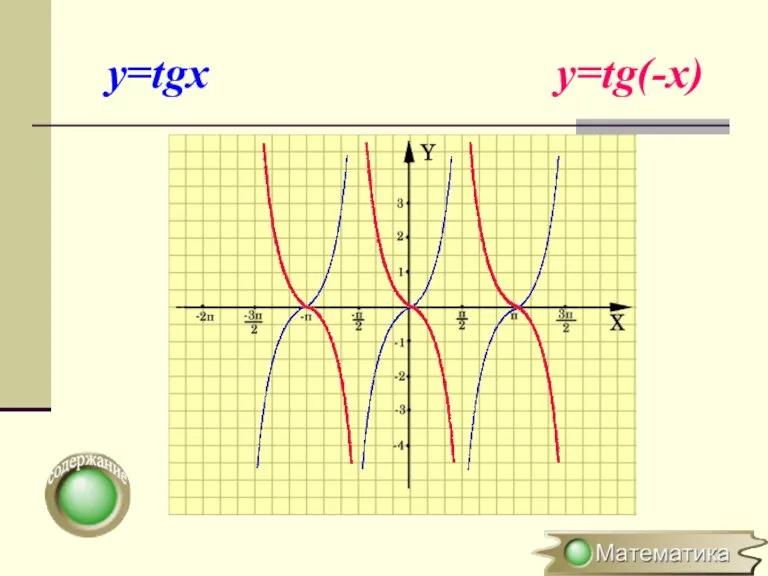
Симметричное отображение относительно оси OХ
y=f(x) → y=f(-x)
(x0;y0) → (-x0;y0) Для построения графика функции y=f(-x) необходимо график функции y=f(x) симметрично отобразить относительно
оси ОY

y=tgx y=tg(-x)

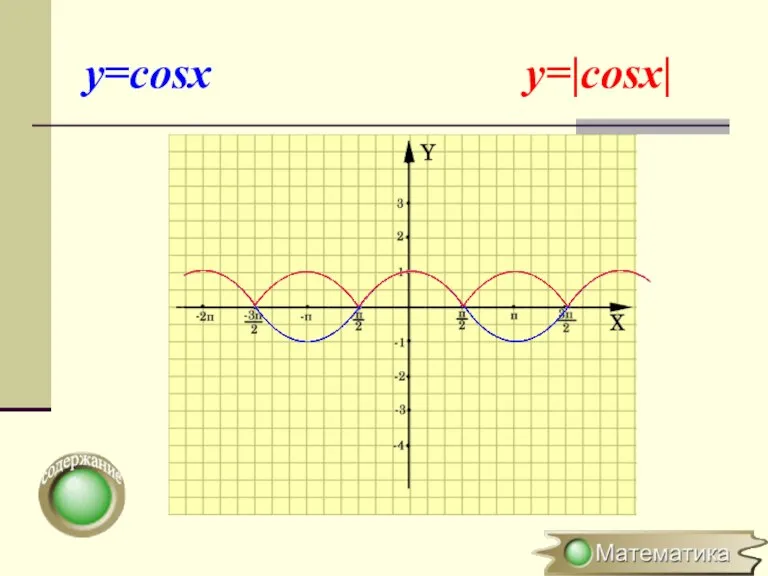
Построение графика y=|f(x)|
Для построения графика функции y=|f(x)| необходимо часть графика функции y=f(x), лежащую выше оси OX, оставить неизменной, а часть графика y=f(x), лежащую ниже оси OХ, симметрично отобразить относительно оси ОХ
f(x), если х 0
y=|f(x)|=
-f(x), если х < 0

y=cosx y=|cosx|

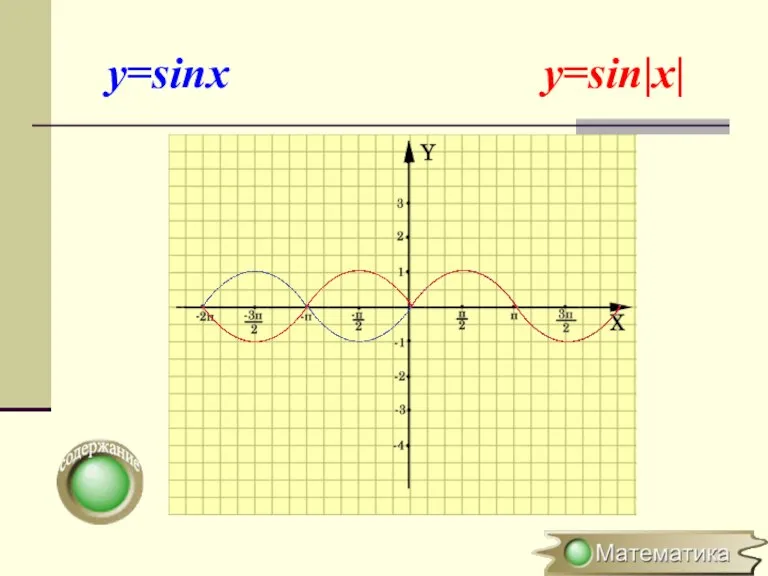
Построение графика y=f(|x|)
f(x), если х 0
y=f(|x|)=
f(-x), если х<0
Для построения графика функции y=|f(x)| необходимо часть графика функции y=f(x), лежащую правее оси OY, оставить неизменной, а часть графика y=f(x), лежащую левее оси OY, симметрично отобразить относительно оси ОY

y=sinx y=sin|x|