Специальные методы решения квадратных уравнений

Рассмотрим решение квадратных уравнений, коэффициенты которых обладают определенными свойствами. Установим связь между суммой коэффициентов уравнения и его корнями.

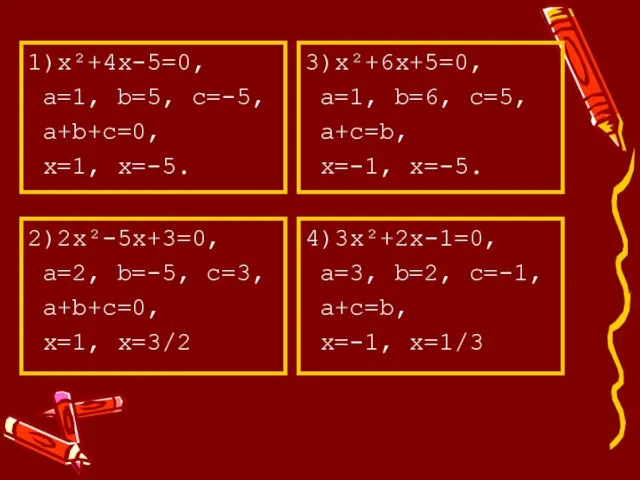
3)х²+6х+5=0,
а=1, b=6, с=5,
а+c=b,
x=-1, x=-5.
1)х²+4х-5=0,
а=1, b=5, с=-5,
а+b+c=0,
x=1, x=-5.
2)2х²-5x+3=0,
a=2, b=-5, c=3,
a+b+c=0,
x=1, x=3/2
4)3х²+2x-1=0,
a=3, b=2, c=-1,
а+c=b,
x=-1, x=1/3

При решении уравнения ax²+bx+c=0 (a≠0) можно пользоваться следующими правилами.
1. Если а+b+c=0, то х=1, х=с/а
2. Если a+c=b, то х=-1, х=-с/а

Докажем утверждение 1.
Разделим обе части уравнения на(a≠0):
x²+(b/a)х+(c/a)=0.
По теореме Виета х1+х2=-b/a, х1*х2=c/a.
Так как а+b+c=0, то b=-a-c, тогда
х1+х2=-(-а-с)/а=1+c/a, х1*х2=1*c/a
значит, х1=1, х2=c/a
Утверждение 2 доказывается аналогично.

Задание (устно).
Найдите корни уравнения:
а) 3х²-8x+5=0;
б) 2х²+3х+1=0;
в) 5х²-9х-14=0;
г) -х²+4х-3=0.
Другой метод решения квадратных уравнений – метод «переброски» старшего коэффициента. Умножим обе части уравнения ax²+bx+c=0 на (a≠0):
a²x²+bax+ca=0.
Пусть ах=у, тогда получим уравнение у²+by+ca=0.
Корни у1 и у2 уравнения найдем по теореме, обратной теореме Виета. Так как ах1=у1, ах2=у2,
то х1=у1/а, х2=у2/а

Пример.
Решите уравнение 2х²-11х+15=0.
Решение: Умножим обе части уравнения на 2:
2²*х²-2*11х+2*15=0.
Пусть 2х=у, тогда у²-11у+30=0.
Корни уравнения: у1=5, у2=6. Тогда 2х1=5, 2х2=6,
откуда х1=5/2, х2=3.
Замечание. Данный метод подходит для квадратных уравнений с «удобными» коэффициентами. В некоторых случаях он позволяет решить уравнение устно.

Задание на дом.
Решите уравнение, выбрав один из специальных методов решения квадратных уравнений:
а) 3х²-5x+2=0
б) 1907х²-101x-2008=0