Содержание
- 2. Познакомимся на примере с возрастанием и убыванием функции. На рисунке ниже изображен график функции, определенной на
- 3. Возрастание и убывание четных функций Для четных функций задача нахождения промежутков возрастания и убывания сильно упрощается.
- 4. Возрастание и убывание функции синус Докажем, что синус возрастает на промеждутках [-π/2+2πn ; π/2+2πn], n -
- 5. Возрастание и убывание функции косинус Промежутками возрастания косинуса являются отрезки [-π+2πn ; 2πn], n - целое.
- 6. Упражнение №82а
- 7. Упражнение №82б
- 8. Упражнение №82в
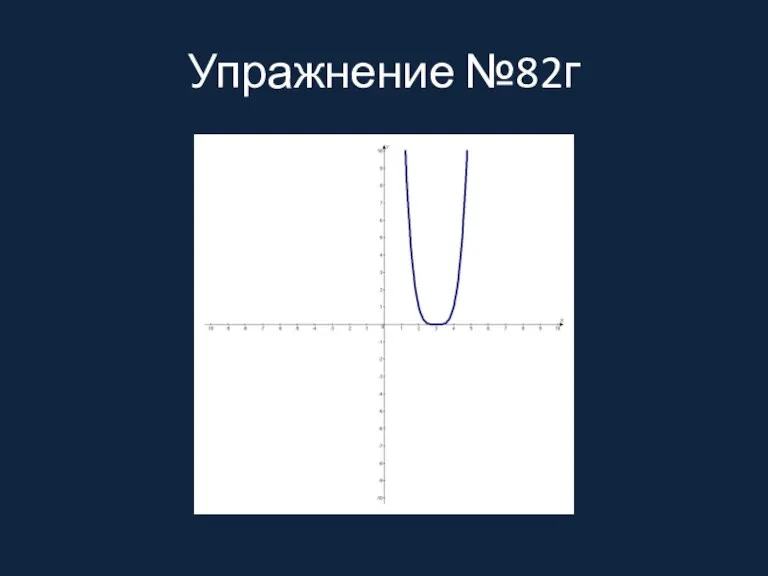
- 9. Упражнение №82г
- 10. Упражнение №83а
- 11. Упражнение №83в
- 12. Упражнение №77,78
- 14. Скачать презентацию
Слайд 2Познакомимся на примере с возрастанием и убыванием функции. На рисунке ниже изображен
Познакомимся на примере с возрастанием и убыванием функции. На рисунке ниже изображен
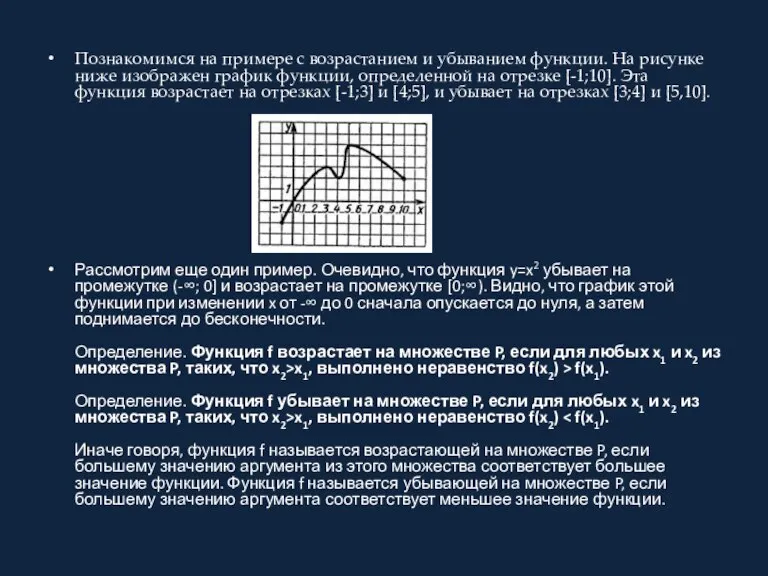
график функции, определенной на отрезке [-1;10]. Эта функция возрастает на отрезках [-1;3] и [4;5], и убывает на отрезках [3;4] и [5,10].
Рассмотрим еще один пример. Очевидно, что функция y=x2 убывает на промежутке (-∞; 0] и возрастает на промежутке [0;∞). Видно, что график этой функции при изменении x от -∞ до 0 сначала опускается до нуля, а затем поднимается до бесконечности. Определение. Функция f возрастает на множестве P, если для любых x1 и x2 из множества P, таких, что x2>x1, выполнено неравенство f(x2) > f(x1). Определение. Функция f убывает на множестве P, если для любых x1 и x2 из множества P, таких, что x2>x1, выполнено неравенство f(x2) < f(x1). Иначе говоря, функция f называется возрастающей на множестве P, если большему значению аргумента из этого множества соответствует большее значение функции. Функция f называется убывающей на множестве P, если большему значению аргумента соответствует меньшее значение функции.
Рассмотрим еще один пример. Очевидно, что функция y=x2 убывает на промежутке (-∞; 0] и возрастает на промежутке [0;∞). Видно, что график этой функции при изменении x от -∞ до 0 сначала опускается до нуля, а затем поднимается до бесконечности. Определение. Функция f возрастает на множестве P, если для любых x1 и x2 из множества P, таких, что x2>x1, выполнено неравенство f(x2) > f(x1). Определение. Функция f убывает на множестве P, если для любых x1 и x2 из множества P, таких, что x2>x1, выполнено неравенство f(x2) < f(x1). Иначе говоря, функция f называется возрастающей на множестве P, если большему значению аргумента из этого множества соответствует большее значение функции. Функция f называется убывающей на множестве P, если большему значению аргумента соответствует меньшее значение функции.
Слайд 3Возрастание и убывание четных функций
Для четных функций задача нахождения промежутков возрастания и
Возрастание и убывание четных функций
Для четных функций задача нахождения промежутков возрастания и

убывания сильно упрощается. Достаточно всего лишь найти промежутки возрастания и убывания при x≥0 (см. рисунок внизу).
Пусть, например, функция f четна и возрастает на промежутке [a;b], где b>a≥0. Докажем, что эта функция убывает на промежутке [-b; -a].
Действительно, пусть -a≥x2>x1≥-b. Тогда f(-x2)=f(x2), f(-x1)=f(x1), причем a≤-x2<-x1≤b, и, поскольку f возрастает на [a;b], имеем f(-x1)>f(-x2), то есть f(x1)>f(x2).
Слайд 4Возрастание и убывание функции синус
Докажем, что синус возрастает на промеждутках [-π/2+2πn ;
Возрастание и убывание функции синус
Докажем, что синус возрастает на промеждутках [-π/2+2πn ;

π/2+2πn], n - целое. В силу периодичности функции синуса доказательство достаточно провести для отрезка [-π/2 ; π/2]. Пусть x2 > x1. Применим формулу разности синусов и найдем:
Из неравенства -π/2 ≤ x1 < x2 ≤ π/2 следует, что и , поэтому и , следовательно и .
Это доказывает, что на указанных промежутках синус возрастает.
Аналогичным образом легко доказать, что промежутки [π/2+2πn ; 3π/2+2πn], n - целое, являются промежутками убывания функции синуса.
Полученный результат можно легко проиллюстрировать с помощью рисунка единичной окружности (см. рисунок ниже). Если -π/2 ≤ t1 < t2 ≤ π/2, то точка Pt2 имеет ординату большую, чем точка Pt1. Если же π/2 ≤ t1 < t2 ≤ 3π/2, то ордината точки Pt2 меньше, чем ордината точки Pt1.
Слайд 5Возрастание и убывание функции косинус
Промежутками возрастания косинуса являются отрезки [-π+2πn ;
Возрастание и убывание функции косинус
Промежутками возрастания косинуса являются отрезки [-π+2πn ;

2πn], n - целое. Промежутками убывания косинуса являются отрезки [2πn ; π + 2πn], n - целое. Доказательство этих утверждений можно провести аналогично доказательству для синуса.
Однако, проще воспользоваться формулой приведения cos(x) = sin(x + π/2), из которой сразу следует, что промежутками возрастания косинуса являются промежутки возрастания синуса, сдвинутые на π/2 влево. Аналогичное утверждение можно сделать и для промежутков убывания.
Слайд 6Упражнение №82а
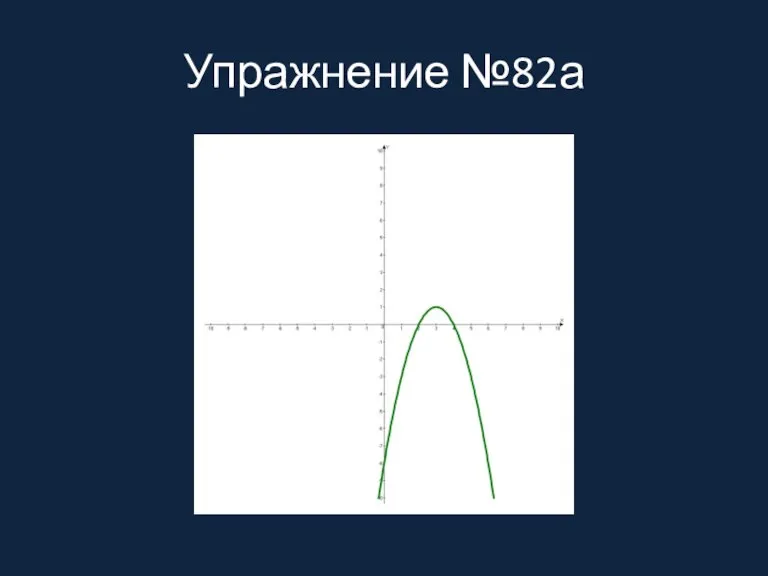
Упражнение №82а
Слайд 7Упражнение №82б
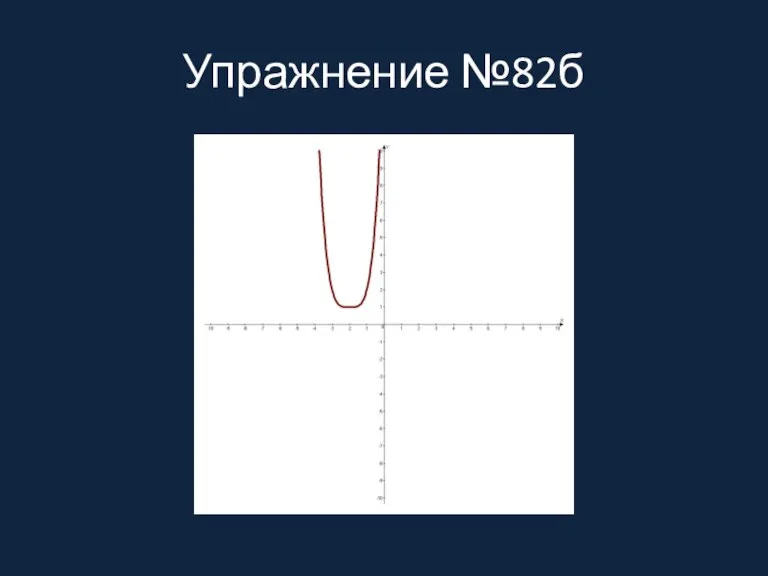
Упражнение №82б
Слайд 8Упражнение №82в
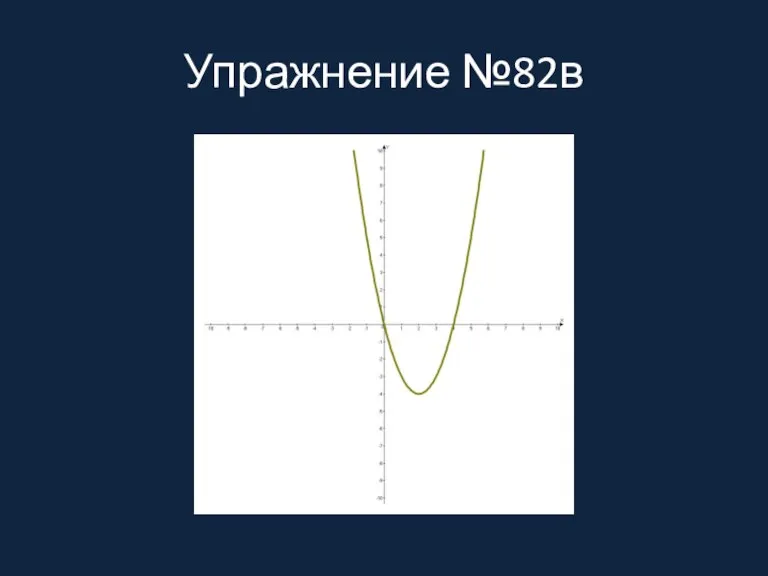
Упражнение №82в
Слайд 9Упражнение №82г
Упражнение №82г
Слайд 10Упражнение №83а
Упражнение №83а

Слайд 11Упражнение №83в
Упражнение №83в

Слайд 12Упражнение №77,78
Упражнение №77,78

Следующая -
Удивительные квадратные уравнения Шарады, метаграммы, логогрифы
Шарады, метаграммы, логогрифы Формулы приведения
Формулы приведения Интегралы
Интегралы Алгебраические дроби
Алгебраические дроби  Линейные уравнения ax=b
Линейные уравнения ax=b Логарифмы. Логарифмическая функция 10 класс
Логарифмы. Логарифмическая функция 10 класс Эпоха Просвещения в России
Эпоха Просвещения в России Задачи с параметрами. Тест. Создано учителем математики школы № 327 Марковой Н.А.
Задачи с параметрами. Тест. Создано учителем математики школы № 327 Марковой Н.А. Таблицы истинности
Таблицы истинности Теорема Виета (8 класс)
Теорема Виета (8 класс) Preobrazovanie-dvoynyh-radikalov.ppt
Preobrazovanie-dvoynyh-radikalov.ppt Решение заданий В9
Решение заданий В9 Алгебра и начала анализа
Алгебра и начала анализа Интеграл
Интеграл Свойства степени
Свойства степени Презентация на тему Как связаны неживая и живая природа
Презентация на тему Как связаны неживая и живая природа  Уравнения, приводимые к квадратным
Уравнения, приводимые к квадратным Линейное уравнение с одним неизвестным
Линейное уравнение с одним неизвестным Тема: «Одночлены»
Тема: «Одночлены» Презентация на тему Таможня в 21-ом веке
Презентация на тему Таможня в 21-ом веке Классная работа. Пропорции. 11.01.13
Классная работа. Пропорции. 11.01.13 Степень с натуральным и целым показателем
Степень с натуральным и целым показателем Квадратные уравнения
Квадратные уравнения Применение неравенств и их свойств
Применение неравенств и их свойств Свойства корня n-ой степени
Свойства корня n-ой степени Формула корней квадратного уравнения
Формула корней квадратного уравнения Metod-racionalizacii.pptx
Metod-racionalizacii.pptx Презентация на тему Виды и особенности экологических правоотношений
Презентация на тему Виды и особенности экологических правоотношений