Математический язык. Математическая модель

Цели:
19.04.2012
Дать понятие об уравнении и его корнях.
Дать понятие о линейном уравнении и его решении.
Текстовые задачи и их решение с помощью уравнений.

19.04.2012
Одной из самых простых и важных математических моделей реальных ситуаций есть линейные уравнения с одной переменной.
3х = 12
5у - 10 = 0
2а +7 = 0
Решить линейное уравнение с одной
переменной – это значит найти те значения
переменной, при каждом из которых
уравнение обращается в верное числовое
равенство.

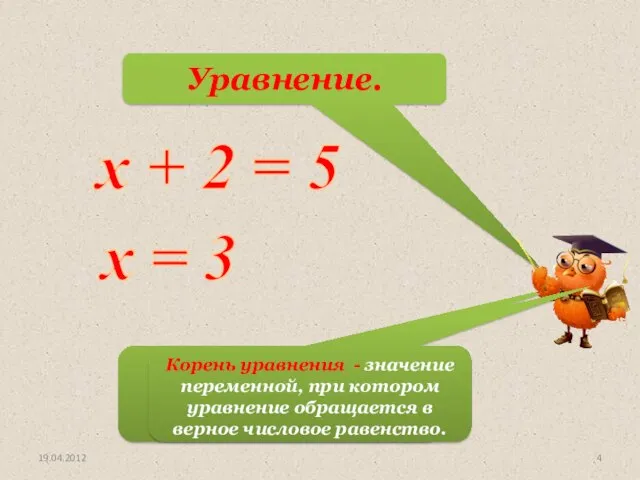
х + 2 = 5
х = 3
Уравнение.
Корень уравнения.
19.04.2012
Корень уравнения - значение переменной, при котором уравнение обращается в верное числовое равенство.

Найдём корень уравнения:
х + 37 = 85
х
37
85
=
_
х = 48
Мы решили уравнение!
19.04.2012
Решили уравнение – нашли те значения переменной, при котором уравнение обращается в верное числовое равенство.

Не решая уравнений, проверь, какое из чисел является корнем уравнения.
42;
0;
14;
12
87 + (32 – х) = 105
19.04.2012

42;
0;
14;
12
87 + (32 – 14) = 105
87 + (32 – 42) = 77
87 + (32 – х) = 105
87 + (32 – 0) = 119
87 + (32 – 12) = 107
х = 14
19.04.2012

Решим уравнение:
(35 + у) – 15 = 31
y = 11
19.04.2012
35 + у
=
31
+
15
35 + у
=
46
y = 46 -35
Решить уравнение – это значит найти все его корни или доказать, что их нет

19.04.2012
Каждое уравнение имеет одни и
те же корни
х₁ = 2 х₂ = 3
Уравнения, которые имеют одни и
те же корни, называют
равносильными.

19.04.2012
При решении уравнений используют
свойства:
Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится
равносильное уравнение.
2. Если обе части уравнения умножить или
разделить на число (не равное нулю), то
получится равносильное
уравнение.

Решите уравнение и выполните проверку:
у - 35 + 12 = 32;
у – 23 = 32;
у = 32 + 23;
у = 55;
(55 - 35) + 12 = 32;
30 + 12 = 32;
32 = 32.
(у - 35) + 12 = 32;
Решение.
Ответ: 55.
19.04.2012
Решение уравнений состоит в постепенной замене более простыми равносильными уравнениями

Решите уравнение и выполните проверку:
24 - 21 + х = 10;
х + 3 = 10;
х = 10 - 3;
х = 7
(24 + 7) - 21 = 31 - 21 = 10;
Ответ: 7.
б) (24 + х) - 21 = 10;
Решение.
19.04.2012
Решение уравнений состоит в постепенной замене более простыми равносильными уравнениями

19.04.2012
Решите уравнение и выполните проверку:
45 + 18 - у = 58;
63 - у = 58;
у = 63 - 58;
у = 5
(45 - 5) + 18 = 40 + 18 = 58.
Ответ: 5.
Решение.
в) (45 - у) + 18 = 58;
Решение уравнений состоит в постепенной замене более простыми равносильными уравнениями

19.04.2012
Уравнение вида:
aх + b = 0
называется линейным уравнением с одной переменной (где х – переменная,
а и b некоторые числа).
Внимание!
х – переменная входит в уравнение
обязательно в первой степени.

19.04.2012
Решите уравнение :
2(3х - 1) = 4(х + 3)
Решение уравнений состоит в постепенной замене более простыми равносильными уравнениями.
aх + b = 0
Приведем к стандартному виду:
2(3х - 1) = 4(х + 3)
6х – 2 = 4х + 12
6х – 4х = 2 + 12
2х = 14
х = 14 : 2
х = 7
- уравнение имеет 1 корень

19.04.2012
уравнение имеет бесконечно много корней
Решите уравнение :
2(3х - 1) = 4(х + 3) – 14 + 2х
Приведем к стандартному виду:
aх + b = 0
2(3х - 1) = 4(х + 3) – 14 + 2х
6х – 2 = 4х + 12 – 14 + 2х
6х – 4x - 2х = 2 + 12 – 14
0 · x = 0
При подстановке любого значения х получаем
верное числовое равенство:
0 = 0
x – любое число
(а = 0, b = 0)

19.04.2012
Уравнение корней не имеет
Решите уравнение :
2(3х - 1) = 4(х + 3) + 2х
Приведем к стандартному виду:
aх + b = 0
2(3х - 1) = 4(х + 3) + 2х
6х – 2 = 4х + 12 + 2х
6х – 4x - 2х -2 - 12 = 0
0 · x - 14 = 0
При подстановке любого значения х получаем
неверное числовое равенство:
-14 = 0
(а = 0, b = -14)

19.04.2012
Вспомним!
При решении задачи четко выполнены три этапа:
Получение математической модели.
Обозначают неизвестную в задаче величину буквой,
используя эту букву, записывают другие величины,
составляют уравнение по условию задачи.
2) Работа с математической моделью.
Решают полученное уравнение,
находят требуемые по условию задачи величины.
3) Ответ на вопрос задачи.
Найденное решение используют для ответа на вопрос задачи
применительно к реальной ситуации.
Математическая модель позволяет анализировать
и решать задачи.

19.04.2012
Задача:
Три бригады рабочих изготавливают игрушки к Новому году. Первая бригада
сделала шары. Вторая бригада изготавливает сосульки и сделала их на 12 штук больше, чем шаров. Третья бригада изготавливает снежинки и сделала их на 5 штук меньше, чем изготовлено шаров и сосулек вместе. Всего было сделано 379 игрушек. Сколько в отдельности изготовлено шаров, сосулек и снежинок?
Шары –
Сосульки –
Снежинки -
?
?
на 12 шт. больше, чем
?
?
- на 5 шт. меньше, чем
Получение математической модели.
Обозначим шары –
сосульки –
снежинки -
х (шт.)
х + 12 (шт.)
х + х + 12 = 2х + 12 (шт.)
2х + 12 – 5 = 2х + 7 (шт.)
Так как по условию всего было сделано 379 игрушек, то составим уравнение:
х + (х + 12) + (2х + 7) = 379
линейное уравнением с одной переменной

19.04.2012
2) Работа с математической моделью.
х + ( х + 12) + (2х + 7) = 379
х + х + 12 + 2х + 7 = 379
Решение уравнений состоит в постепенной замене более простыми равносильными уравнениями.
Приведем к стандартному виду:
aх + b = 0
4х + 19 = 379
4х = 379 - 19
4х = 360
х = 360 : 4
х = 90
90 шт. - шаров
х + 12 = 90 + 12 = 102 (шт.) - сосульки
2х + 7 = 2 · 90 + 7 = 187 (шт.) - снежинок
3) Ответ на вопрос задачи:
90 шт. – шаров,
102 (шт.) – сосульки,
187 (шт.) - снежинок