Содержание
- 2. Вариант 1 Самостоятельная работа x³ y = e y = ln (x² +1) Построить график функции
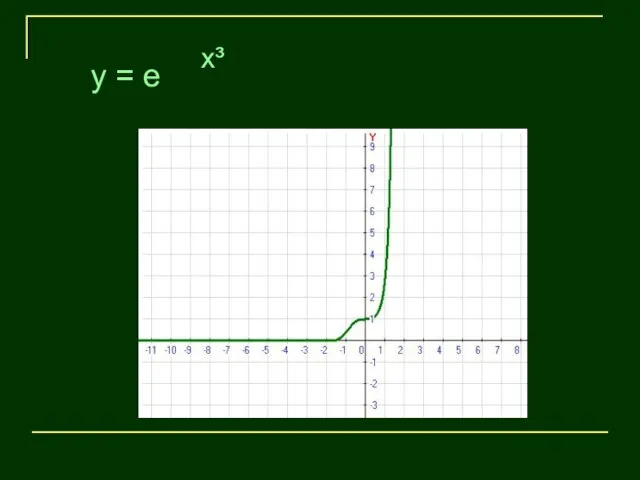
- 3. x³ y = e
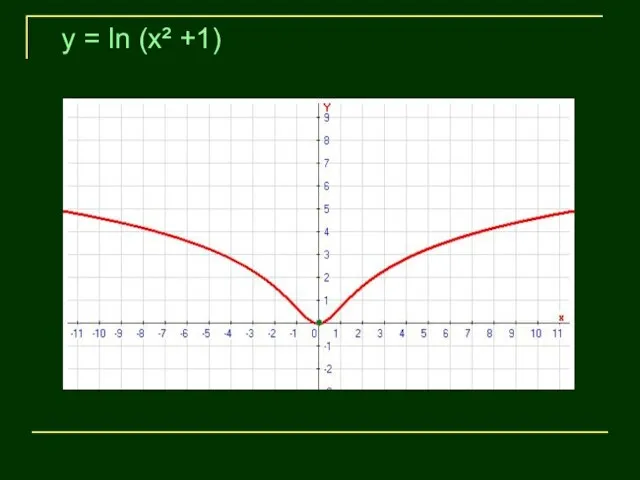
- 4. y = ln (x² +1)
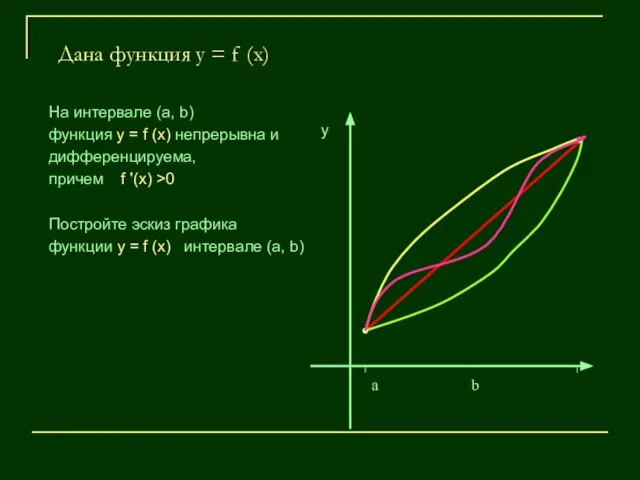
- 5. Дана функция у = f (x) На интервале (а, b) функция у = f (x) непрерывна
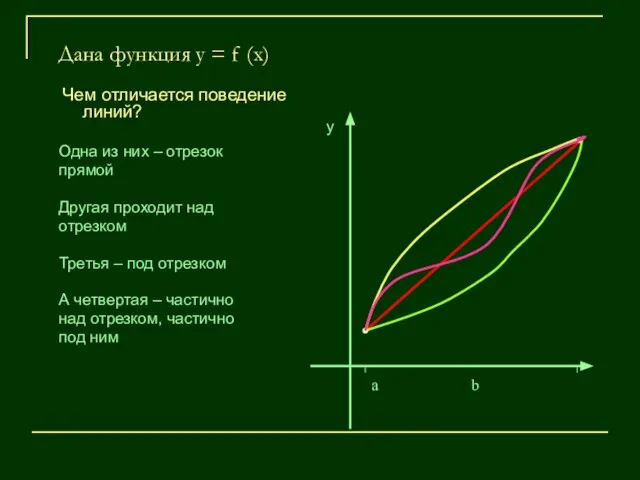
- 6. Дана функция у = f (x) Чем отличается поведение линий? Одна из них – отрезок прямой
- 7. В математике для обозначения такого поведения существуют специальные понятия: выпуклости и вогнутости графика функции
- 8. Выпуклость и вогнутость функции Геометрический смысл второй производной
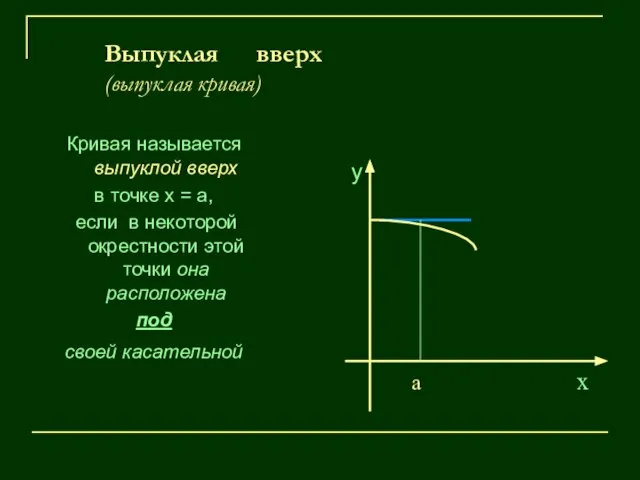
- 9. Выпуклая вверх (выпуклая кривая) Кривая называется выпуклой вверх в точке х = а, если в некоторой
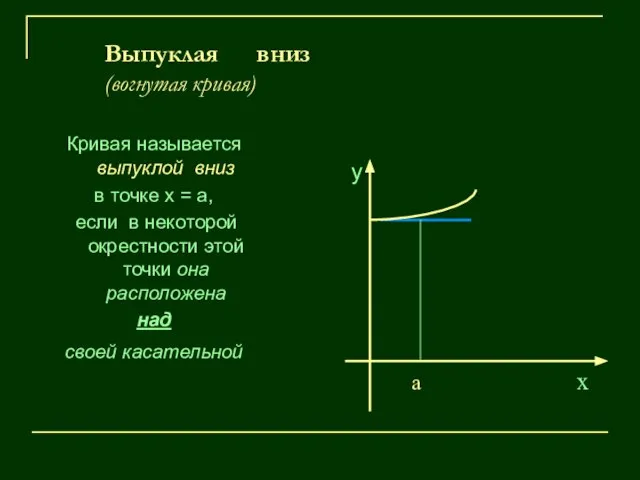
- 10. Выпуклая вниз (вогнутая кривая) Кривая называется выпуклой вниз в точке х = а, если в некоторой
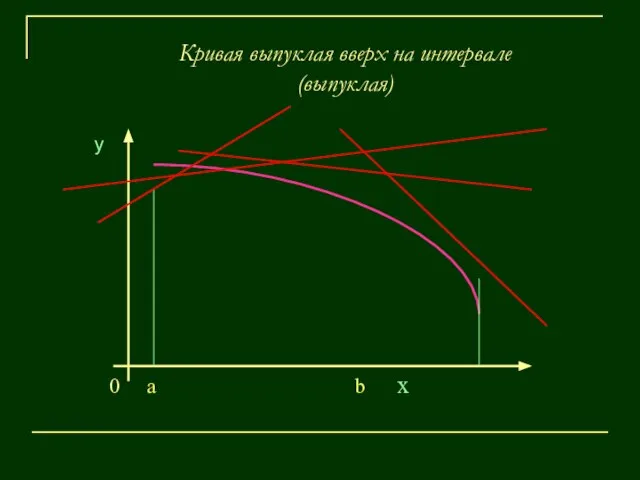
- 11. Кривая выпуклая вверх на интервале (выпуклая) у 0 a b х
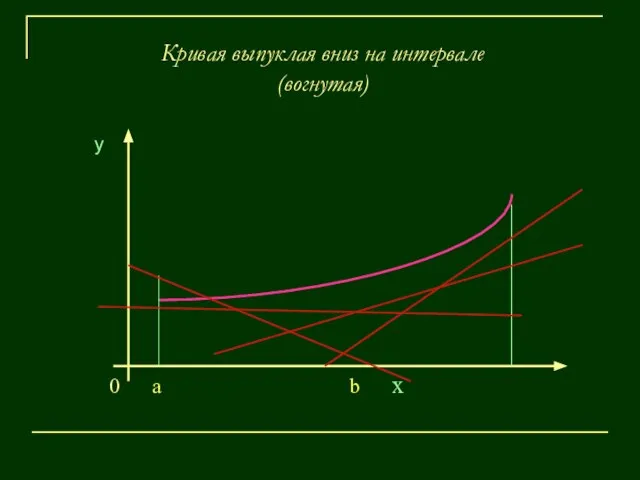
- 12. Кривая выпуклая вниз на интервале (вогнутая) у 0 a b х
- 13. Как найти интервалы выпуклости и вогнутости?
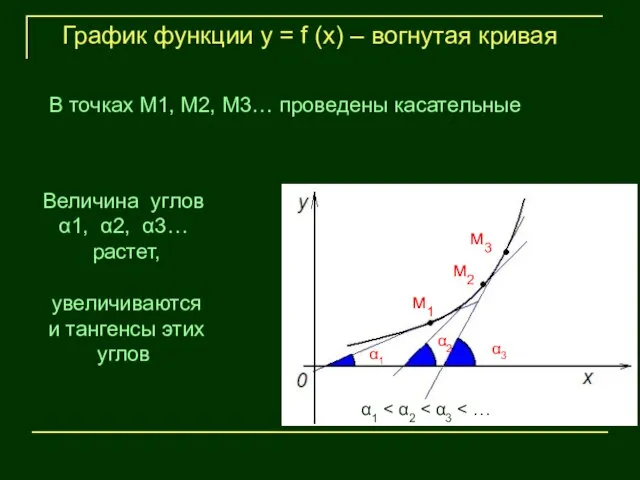
- 14. м1 м2 м3 α1 α2 α3 График функции у = f (х) – вогнутая кривая Величина
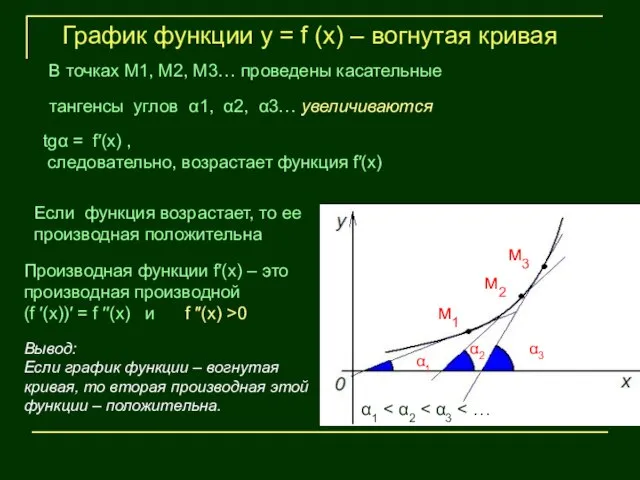
- 15. м1 м2 м3 α1 α2 α3 График функции у = f (х) – вогнутая кривая В
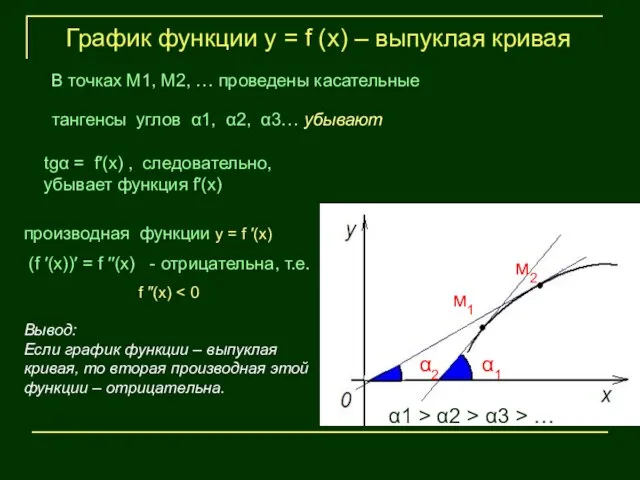
- 16. α1 График функции у = f (х) – выпуклая кривая tgα = f′(х) , следовательно, убывает
- 17. Если вторая производная функции у = f (х) на данном интервале положительна, то кривая вогнута а
- 18. Точки, в которых выпуклость меняется на вогнутость или наоборот, называются точками перегиба
- 19. Правило нахождения интервалов выпуклости и вогнутости графика функции: Найти: Вторую производную Точки, в которых она равна
- 20. Исследование функции с помощью второй производной Интервалы выпуклости: (-3, 0) и (2, 5) Интервалы вогнутости: (-∞,
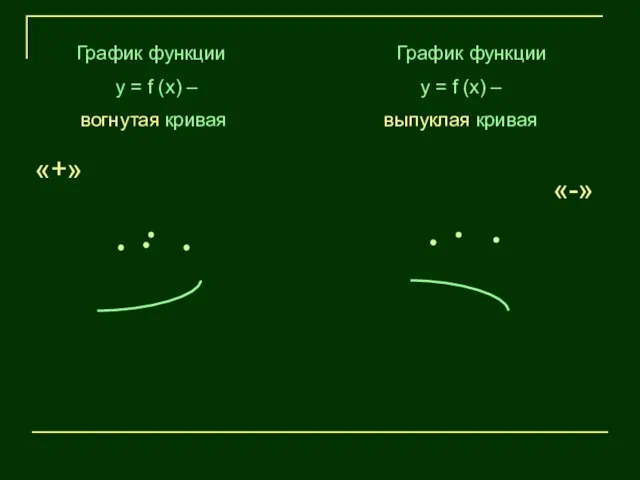
- 21. График функции у = f (х) – вогнутая кривая График функции у = f (х) –
- 22. Найти интервалы выпуклости и вогнутости и точки перегиба Вариант 1 у = х³ - 12х +
- 23. Проверка Вариант 1 у = х³ - 12х + 4 х – любое число f'(х) =
- 24. Проверка Вариант 2 у = ¼ х4 – 3/2 х² х – любое число f'(х) =
- 26. Скачать презентацию











 Функции. Графики функций 7 класс
Функции. Графики функций 7 класс Краснооктябрьская средняя общеобразовательная школа, Республика Марий Эл Старикова Г.А., учитель высшей категории.
Краснооктябрьская средняя общеобразовательная школа, Республика Марий Эл Старикова Г.А., учитель высшей категории.  ТЕМА УРОКА: РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ ПО ФОРМУЛЕ.
ТЕМА УРОКА: РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ ПО ФОРМУЛЕ. Что такое функция?
Что такое функция? Lineynye-uravneniya-s-odnoy-peremennoy.pptx
Lineynye-uravneniya-s-odnoy-peremennoy.pptx Презентация на тему Ответственность за несвоевременную или неправильную уплату таможенных платежей
Презентация на тему Ответственность за несвоевременную или неправильную уплату таможенных платежей Квадратичная функция (8 класс)
Квадратичная функция (8 класс) Презентация на тему Научная революция 20 века
Презентация на тему Научная революция 20 века  Презентация на тему Аварии на радиационно-опасных объектах
Презентация на тему Аварии на радиационно-опасных объектах  Франсуа Виет 1540 - 1603
Франсуа Виет 1540 - 1603 Особые приёмы решения логарифмических неравенств с переменной в основании Занятие №3
Особые приёмы решения логарифмических неравенств с переменной в основании Занятие №3 Презентация на тему Буддизм
Презентация на тему Буддизм  Законы булевой алгебры
Законы булевой алгебры Логарифмы. Логарифмическая функция 10 класс
Логарифмы. Логарифмическая функция 10 класс Преобразования графиков функций 10 класс
Преобразования графиков функций 10 класс Преобразование графиков тригонометрических функций
Преобразование графиков тригонометрических функций Виды показательных уравнений
Виды показательных уравнений  Алгебра логики. Понятие высказывания
Алгебра логики. Понятие высказывания Крестовые походы
Крестовые походы Тригонометрические уравнения
Тригонометрические уравнения  Урок в 11 классе. Урок в 11 классе. Составила учитель Кировской МБОУ Ткачук Н. П.
Урок в 11 классе. Урок в 11 классе. Составила учитель Кировской МБОУ Ткачук Н. П.  ГИА 2013 Модуль «АЛГЕБРА» №2
ГИА 2013 Модуль «АЛГЕБРА» №2 Системы двух линейных уравнений с двумя переменными
Системы двух линейных уравнений с двумя переменными Понятие бесконечной интегральной суммы. Интеграл
Понятие бесконечной интегральной суммы. Интеграл Алгебраическая дробь. Сокращение дробей
Алгебраическая дробь. Сокращение дробей Свойства функции Алгебра 9 класс
Свойства функции Алгебра 9 класс  Решение систем линейных уравнений с двумя неизвестными
Решение систем линейных уравнений с двумя неизвестными Свойства и график функции СИНУС
Свойства и график функции СИНУС