Квадрат суммы. Квадрат разности 7 класс

Тема урока:
Квадрат суммы.
Квадрат разности.

Цель урока:
Познакомиться с формулами квадрата суммы и квадрата разности и их применением для разложения выражений на множители и упрощения вычислений.

Задачи урока:
1. Развивающая - познакомиться с более легким способом алгебраических вычислений, вывести формулы квадрата суммы и квадрата разности двух чисел.
2. Образовательная - приобрести навык вычисления по формулам квадрата суммы и квадрата разности двух чисел, учиться выявлять главные и определенные закономерности.
3. Воспитательная -осознать ценность и необходимость полученных знаний, сопереживать за достижения своих товарищей.

УСТНЫЙ СЧЁТ:
Возвести в квадрат:
a; 4а; 3c; 8с²k³; 5с4k6 ; 10pd6
ОТВЕТЫ:
a2 ; 16а2; 9c2; 64с4 k6; 25с8k12 ; 100p2d12

УСТНЫЙ СЧЁТ:
Найдите число, которое в квадрате даст
100; 25a2 ; 81х2у4 ; 49k6 d10
ОТВЕТЫ:
10; 5a ; 9ху2 ; 7k3d5

УСТНЫЙ СЧЁТ:
Найдите удвоенное произведение выражений:
a и b, 0,5c и 6,
4x и 2x², 2b и -5k
Ответы:
2ab, 3c, 8x3, -10 bk

Сформулируйте правило умножения многочлена на многочлен?
Рассмотрим квадрат суммы двух чисел (a+b)2 и пользуясь правилом умножения многочлена на многочлен, получаем:
(a+b)2 =(a+b)(a+b)= a2+ab+ab+b2 = a2+2ab+b2

Получаем
ФОРМУЛУ КВАДРАТА СУММЫ
(a+b)2 =a2+2ab+b2
Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе и плюс квадрат второго числа.

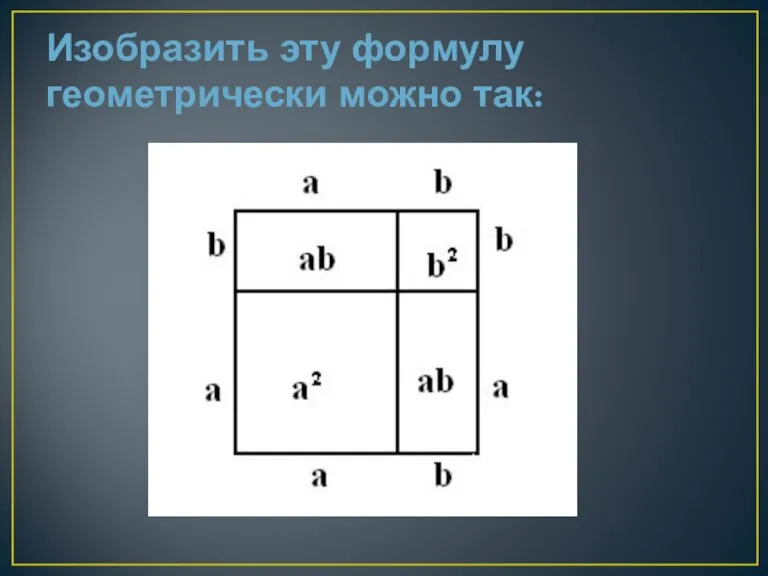
Изобразить эту формулу геометрически можно так:

ФОРМУЛА КВАДРАТА РАЗНОСТИ
(a-b)2 =a2-2ab+b2
Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого числа на второе и плюс квадрат второго числа.

ВАЖНО!
а и b в формулах могут быть любыми числами или алгебраическими выражениями

ФОРМУЛЫ СОКРАЩЁННОГО УМНОЖЕНИЯ:
(a+b)2 =a2+2ab+b2
(a-b)2 =a2-2ab+b2

Формулы сокращённого умножения применяются в некоторых случаях для упрощения вычислений.
Например:
992 =(100-1)2 =102 -2*100*1+12 =
10 000-200+1=9801
(50+2)2=502 +2*50*2+22=
2500+200+4=2704

Преобразуем выражение в виде многочлена:
(2m+3k)² =
(2m)2+2●2m●3k+(3k)2=4m2+12mk+9k2
(5a2-3)² =
(5a)2-2● 5a2●3+32=25a4 -30a2+9

Вылечи равенство:
(a-2b)2= a2- *ab+4b2
(2a+0,5b)2= 4a2+2ab+*b2
9d2- 12dc+*c2= (3d-2c)2
(4k+2m)2= *k2+16km+4m2

Представить квадрат двучлена в виде многочлена:
№370
1) (c+d)²
(x-y)²
(2+x)²
4) (x+1)²

РЕЗУЛЬТАТ:
1) (c+d)² = c2+2cd+d2
2) (x-y)² = x2-2xy+y2
3) (2+x)² = 4+4x+x2
4) (x+1)² = x2+2x+1

ВЫЧИСЛИТЬ:
№374 №375
(90-1)² 72²
(40+1)² 57²
101² 997²
98² 1001²

РЕЗУЛЬТАТ:
№374 №375
7921 5184
1681 3249
10 201 994 009
9604 1 002 001

Применив формулы, заполните таблицу:

Результаты:

Итоги урока:
Что нового вы узнали сегодня на уроке?
Для чего необходимо знать изученные нами сегодня формулы?
Как вы думаете, почему данные формулы называются формулами сокращённого умножения?

Домашнее задание:
§ 22 страницы 90-92. Прочитать и выучить словесные формулировки формул.
№ 379, №380.