Логарифмы. Применение логарифмов - презентация по Алгебре_

повторить определение логарифма;
закрепить основные свойства логарифмов;
- способствовать формированию умения применять свойства логарифмов при упрощении выражений;
- развивать математическое мышление; технику
вычисления; умение логически мыслить
и рационально работать;
- воспитание познавательной активности, чувства
ответственности, уважения друг к другу.
Цели урока:

ДЖОН НЕПЕР
(1550-1617)
Шотландский математик –
изобретатель логарифмов.
В 1590-х годах пришел к идее
логарифмических вычислений
и составил первые таблицы
логарифмов, однако свой знаменитый
“Описание удивительных таблиц логарифмов” опубликовал лишь в 1614 году.
Ему принадлежит определение логарифмов, объяснение их свойств, таблицы логарифмов синусов, косинусов, тангенсов и приложения логарифмов в сферической тригонометрии.

Разминка

1. Логарифмом числа b по …………… а
называется …………….. степени, в которую
нужно……………. основание а, чтобы
получить число b.
2. Основание и число, стоящее под знаком
логарифма, должны быть………….
3. Если основание а =….., то такой логарифм
называется десятичным и обозначается lg b.
основанию
показатель
возвести
положительными
10
Продолжи предложение.....

Установите соответствие

1
9
8
1
9
2
8
2
Обгонялки

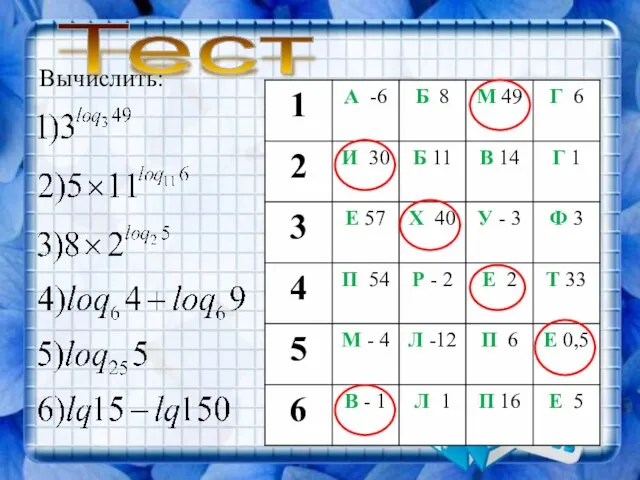
Вычислить:
Тест

Музыканты редко увлекаются математикой. Большинство из них питают к этой науке чувство уважения. Между тем, музыканты – даже те, которые не проверяют подобно Сальери у Пушкина “алгеброй гармонию”, встречаются с математикой гораздо чаще, чем сами подозревают, и притом с такими “странными” вещами, как логарифмы.
Применение логарифмов

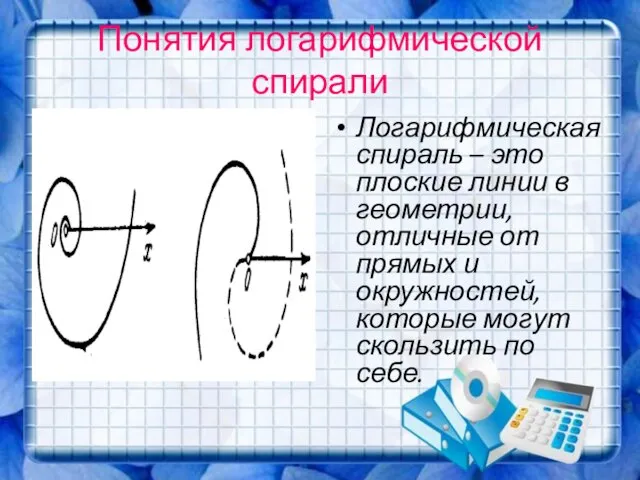
Понятия логарифмической спирали
Логарифмическая спираль – это плоские линии в геометрии, отличные от прямых и окружностей, которые могут скользить по себе.

Семечки в подсолнухе
расположены
по дугам, так же близким к
логарифмической спирали.
Поэтому раковины многих моллюсков, улиток, а так же рога таких млекопитающих как архары (горные козлы), закручены по логарифмической спирали.
Семечки в подсолнухе
расположены
по дугам, так же близким к
логарифмической спирали.

Раковины морских животных могут расти лишь в одном направлении. Чтобы не слишком вытягиваться им приходиться скручиваться, причём каждый следующий виток подобен предыдущему. А такой рост может совершаться лишь по логарифмической спирали, можно сказать что эта спираль является математическим символом соотношения форм роста.

Логарифмическая спираль в природе
Один из наиболее распространенных пауков ЭПЕЙРА, сплетая паутину, закручивает нити вокруг центра по логарифмической спирали.
По логарифмическим спиралям закручены и многие галактики, в частности, галактика которой принадлежит Солнечная Система.

Молекула ДНК
Её молекулы имеют огромную по молекулярным масштабам длину и состоят из 2-х нитей, сплетённых между собой в двойную спираль. Каждую из нитей можно сравнить с длинной нитки бус. С нитями бус мы сравниваем и белки.

Логарифмы в космосе

Яркость звезд составляет геометрическую прогрессию со знаменателем 2,5 легко понять, что «величина» звезды представляют собой логарифм её физической яркости.
Оценивая яркость звезд, астроном оценивает таблицей логарифмов составленной при основании 2,5.
Аналогично оценивается и громкость шума. Вредное влияние промышленных шумов на здоровье рабочих и производстве труда.

н о ь
ч а с т н о о
с у м е
1. loga 1=…..
2. В определении логарифма loga b = x,
число а называется………
о с н в а н и е
3. Разность логарифмов равна логарифму…. .
4. Логарифмом числа b по основанию а, называют
………… степени, в которую нужно возвести а,
чтобы получить b.
п о к з а т е л ь
н е п е
6. Логарифм с основанием 10 называется …..
д е с я т ч н ы й
Кто изобрёл логарифмы?
7. Операцию нахождения логарифма
называют ……….
л о г а р и м и р о в а н и е
8. Логарифм произведения чисел равен …………
логарифмов от этих чисел.
А К З Ы У М
М У З Ы К А
Кроссворд