Последовательности 2011 Васильева Е.Е.

Продолжи ряд
1, 2, 3, 4, 5, 6
12, 10, 8, 6, 4
6, 9, 12, 15, 18, 21
2, 4, 8, 16, 32
1, 4, 16

Последовательности составляют такие элементы природы, которые можно пронумеровать
Дни
недели
Классы
В
школе
Дома
на
улице
Квартиры
в
доме
Номера
счетов
в
банке
Название
месяцев

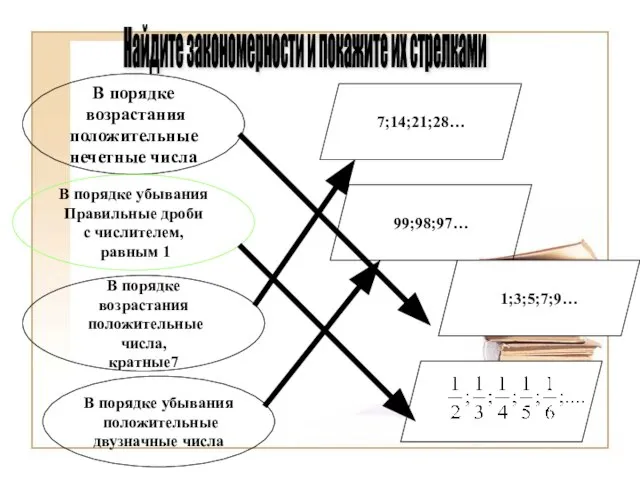
Найдите закономерности и покажите их стрелками
В порядке
возрастания
положительные
нечетные числа
В порядке убывания
Правильные дроби
с числителем,
равным 1
В порядке возрастания
положительные числа,
кратные7
В порядке убывания
положительные
двузначные числа
7;14;21;28…
99;98;97…
1;3;5;7;9…

Определение
Функцию y=f(x), определенную на множестве натуральных чисел xϵN
(или его конечном подмножестве),
называют числовой последовательностью и обозначают
y=f(n), или
y1,y2,…,yn,…. или (yn).

Числа y1, y2, …, yn называют членами последовательности, а член с номером n – ее
n-членом, его еще называют общим членом.

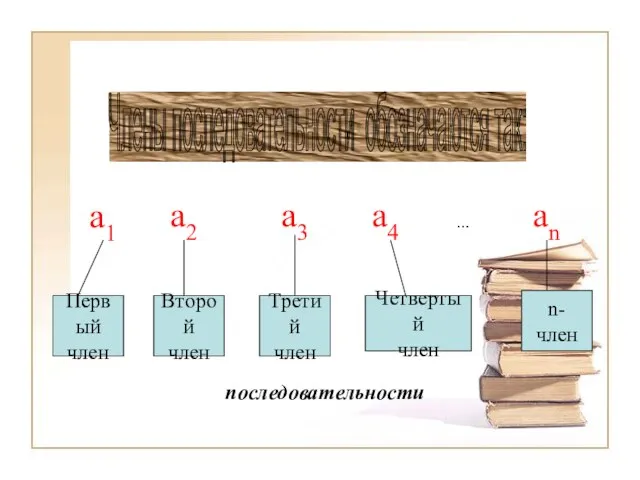
Члены последовательности обозначаются так:
a1
a2
a3
a4
…
an
Первый
член
Второй
член
Третий
член
Четвертый
член
n-член
последовательности

Задать числовую последовательность
— это значит указать, как отыскивается тот или иной ее член, если известен номер занимаемого им места.

Способы описания последовательности
Последовательности можно задавать различными способами, среди которых особенно важны три:
аналитический
словесный
рекуррентный

Формула
1. Последовательность задана аналитически, если задана формула ее n-го члена: yn = f(n).
Пример: yn = 2n – 1
Y1=2*1-1=1
Y2=2*2-1=2
Y3=2*3-1=5
Y4=2*4-1=7
Y5=2*5-1=9
последовательность нечетных чисел:
1, 3, 5, 7, 9, …

Описательный способ задания числовой последовательности состоит в том, что объясняется, из каких элементов строится последовательность.
Пример 1.
«Все члены последовательности равны 1». Это значит, речь идет о стационарной последовательности 1, 1, 1, …, 1, ….
Пример 2.
«Последовательность состоит из всех простых чисел в порядке возрастания». Таким образом, задана последовательность 2, 3, 5, 7, 11, ….

Рекурентный
Рекуррентный способ задания последовательности состоит в том, что указывается правило, позволяющее вычислить n-й член последовательности, если известны ее предыдущие члены.

Пример рекуррентного задания
Пример 1.
y1 = 3;
yn = yn–1 + 4, если n = 2, 3, 4,….
Здесь
y1 = 3;
y2 = 3 + 4 = 7;
y3 = 7 + 4 = 11; ….

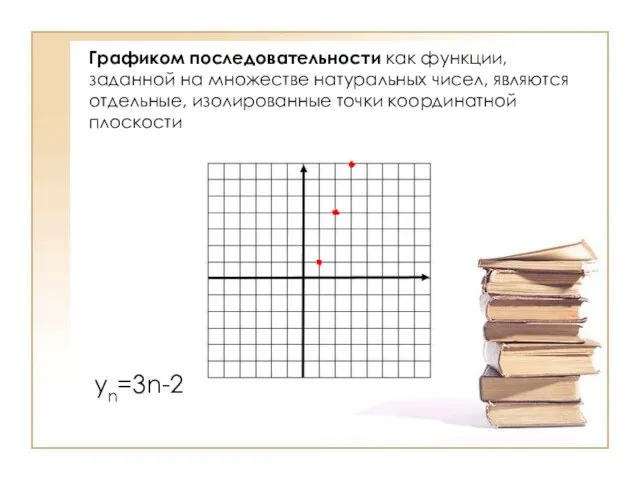
Графиком последовательности как функции, заданной на множестве натуральных чисел, являются отдельные, изолированные точки координатной плоскости
yn=3n-2

задание
Последовательности заданы формулами
an=n4
an=n+4
an=2n-5
an=(-1)nn2
an= -n-2
an=3n-1
1. Впишите пропущенные члены последовательности
1;___;81;___;625;…
5;___;___;___;9
-1;4;___;___; -25;…
-3; -4;___;___; -7…
2; 8;___;___;___...
___;-4;___;___;-7
2. Укажите, какими числами являются члены этих последовательностей
Положительные
и отрицательные
положительные
отрицательные
16
256
-9
16
-5
-6
6
7
8
-3
-5
-6
26
80
242

По преданию, индийский царь Шерам, восхищенный остроумием шахматной игры, призвал к себе изобретателя шахмат Сету и сказал ему: «Я желаю достойно вознаградить тебя ! Исполню любое твое желание…» Сета попросил положить на первую клетку доски 1 пшеничное зерно, на вторую – 2 зерна, на третью – 4 зерна и т. д. Сколько нужно зерен ?

Среднеазиатский математик Бернулли получил верный ответ:
18 446 744 073 709 551 615 зерен.
Такое количество зерен пшеницы можно собрать лишь с урожая планеты, поверхность которой в 2000 раз больше поверхности Земли.

ПРОТОРГОВАЛСЯ ЛИ КУПЕЦ ?
Некто продавал коня и просил за него 1000 рублей. Купец ска­зал, что цена велика, "Хорошо,-ответил продавец, если ты гово­ришь, что конь дорого стоит, то возьми его себе даром, а заплати только за одни гвозди на его подковах, а гвоздей на его каждой подкове по 6 штук, и будешь ты мне за них платить таким образом: за первый гвоздь полушку, за второй - две полушки, за третий 4 полушки, и так далее за все гвозди: за каждый в два раза больше чем предыдущий". Купец согласился, проторговался ли купец?

РЕШЕНИЕ:
всего гвоздей 24 штуки,
за все гвозди купец должен заплатить
1 + 2 + 2*2 + 2*2*2+ +...+2*2*...*2 полушек
23 раза и того получаем 41943 рубля и 15 полушек.

Свойства числовых последовательностей
Числовая последовательность называется возрастающей, если каждый ее член больше предыдущего, иными словами, если для всякого n > 1 верно неравенство an > a n – 1.

Пример
Последовательность кубов натуральных чисел
1,8,27

УБЫВАЮЩАЯ
Числовая последовательность называется убывающей, если каждый ее член (кроме первого) меньше предыдущего, иными словами, если для всякого n > 1 верно неравенство an < a n – 1.

Пример

Монотонность
Вместе возрастающие и убывающие последовательности называются монотонными последовательностями.

Определить монотонность
1)-1,-4,-9,-16….
2)-1,0,1,2….
3)-1,1,-1,1

Ограниченность сверху
Определение. Последовательность a1, a2, a3, … называется ограниченной сверху, если для ее такое число M, что неравенство
an

Пример
1,-1,-3,-5
Ограничена сверху М =1

Ограниченность снизу
Определение. Последовательность a1, a2, a3, … называется ограниченной снизу, если для ее такое число m, что неравенство
an >m выполняется для всех номеров n.

Пример
Ограничена и сверху и снизу
М=1
M=0

Упражнение 1
Укажите номер функции, являющейся числовой последовательностью

Найдите первые пять членов последовательности заданной рекуррентно
Y1=2
Yn=yn-1+5
Упражнение 2

Упражнение 3

Упражнение 4
Укажите номер убывающей последовательности