Слайд 2При изучении логарифмических функций рассматриваются неравенства вида:
logax < b logax ≥

b
Слайд 3logax > logay
x>0; y>0
eсли а>0, то x>y
eсли 0
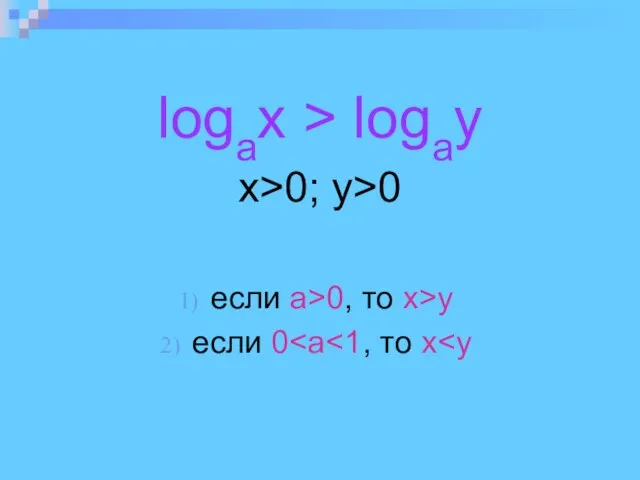
Слайд 4Пример №1
Решить неравенство: log 3(x+2)<3
log 3(x+2)a=3; 3>0 => функция возрастает
x+2<27
x+2<27

x<25
x+2>0 x>-2
Ответ: (-2;25)
Слайд 5Пример №2
Решить неравенство:log0,5(2x+1)>-2
a=0,5; 0<0,5<1 => функция убывает
log0,5 (2x+1)> log0,54

2x+1<4
2x+1<4 2x<3 x<1,5
2x+1>0 2x>-1 x>-0,5
Ответ: (-0,5;1,5)
Слайд 6Решите устно:
log2x>1 ответы:
(2;∞)
log3x>2
(9;∞)
log5x≥0
[1;∞)
log0,5x≥0
(-∞;1]
![Решите устно: log2x>1 ответы: (2;∞) log3x>2 (9;∞) log5x≥0 [1;∞) log0,5x≥0 (-∞;1]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/475057/slide-5.jpg)
Слайд 7log2x≤1 ответы:
(0;2]
log3x<2
(0;9)
log2x<1/2
(0;√2)
log3x<0
(0;1)
![log2x≤1 ответы: (0;2] log3x (0;9) log2x (0;√2) log3x (0;1)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/475057/slide-6.jpg)
Слайд 8Решите неравенства:
log3(x-2)>1
a>1 = >функция возрастает
x-2>3
x-2>3 x>5
x-2>0 x>2
ответ: (5;∞)
log2(x-3)>5
a>1

= >функция возрастает
x-3>32
x-3>32 x>35
x-3>0 x>3
ответ: (35;∞)

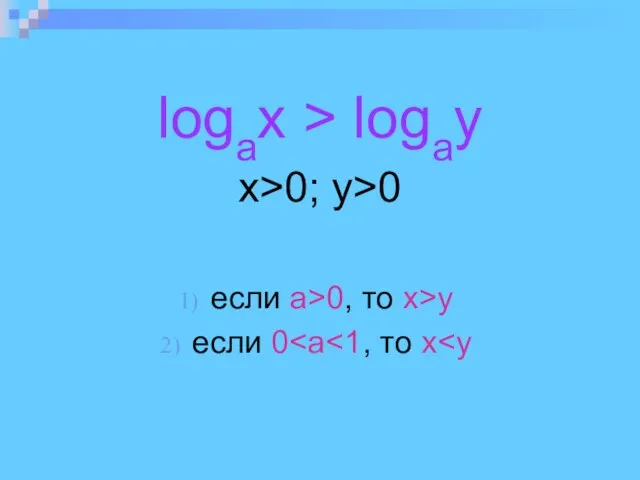


![Решите устно: log2x>1 ответы: (2;∞) log3x>2 (9;∞) log5x≥0 [1;∞) log0,5x≥0 (-∞;1]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/475057/slide-5.jpg)
![log2x≤1 ответы: (0;2] log3x (0;9) log2x (0;√2) log3x (0;1)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/475057/slide-6.jpg)

 Способы задания последовательностей
Способы задания последовательностей  Понятие производной
Понятие производной Математика и естественные науки
Математика и естественные науки Решение неравенств методом интервалов (9 класс)
Решение неравенств методом интервалов (9 класс) Экскурсия в историю математики
Экскурсия в историю математики Урок по теме: “Тригонометрические формулы.” Ельцова Н.Г.,учитель МОУ «Гимназия №11», Г Норильск.
Урок по теме: “Тригонометрические формулы.” Ельцова Н.Г.,учитель МОУ «Гимназия №11», Г Норильск. В6 элементы теории вероятностей ГБОУ школа №255 Учитель математики Булатова Л.А.
В6 элементы теории вероятностей ГБОУ школа №255 Учитель математики Булатова Л.А. Преобразование выражений, содержащих квадратные корни. Презентацию подготовила учитель математики Пухальская Надежда Алек
Преобразование выражений, содержащих квадратные корни. Презентацию подготовила учитель математики Пухальская Надежда Алек Алгебра и начала анализа
Алгебра и начала анализа Наглядное представление статистической информации
Наглядное представление статистической информации Прогрессия - движение вперёд !
Прогрессия - движение вперёд ! Funkcii-i-ih-svoystva-funkcionalnye-uravneniya.ppt
Funkcii-i-ih-svoystva-funkcionalnye-uravneniya.ppt Toplivno-energeticheskii_774_komplex_Rossii_9_klass_Prezentatsia_k_otkrytomu_uroku.pptx
Toplivno-energeticheskii_774_komplex_Rossii_9_klass_Prezentatsia_k_otkrytomu_uroku.pptx Презентация на тему Собор святой Софии в Константинополе
Презентация на тему Собор святой Софии в Константинополе  Сложение чисел с разными знаками. 6 класс Новосёлова Е.А. МОУ «Усть-Мосихинская СОШ»
Сложение чисел с разными знаками. 6 класс Новосёлова Е.А. МОУ «Усть-Мосихинская СОШ» Квадратные уравнения
Квадратные уравнения Производная функции
Производная функции Презентация на тему Основные проблемы применения коллизионного регулирования и способы их разрешения
Презентация на тему Основные проблемы применения коллизионного регулирования и способы их разрешения Функции и их графики 10 класс
Функции и их графики 10 класс Название презентации
Название презентации Применение производной для исследования функций. 1. Нахождение промежутков возрастания функции. 2. Нахождение промежутков убыв
Применение производной для исследования функций. 1. Нахождение промежутков возрастания функции. 2. Нахождение промежутков убыв Презентация на тему МАТРЁНА, МАТРЁША, МАТРЁШЕЧКА
Презентация на тему МАТРЁНА, МАТРЁША, МАТРЁШЕЧКА  Презентация на тему: Применение производной
Презентация на тему: Применение производной Делители и кратные (6 класс)
Делители и кратные (6 класс) Преобразование двойных радикалов 8 класс
Преобразование двойных радикалов 8 класс Старинные ЗАНИМАТЕЛЬНЫЕ задачи
Старинные ЗАНИМАТЕЛЬНЫЕ задачи Натуральные логарифмы
Натуральные логарифмы Методы решения уравнений
Методы решения уравнений