koren-n-oy-stepeni.pptx

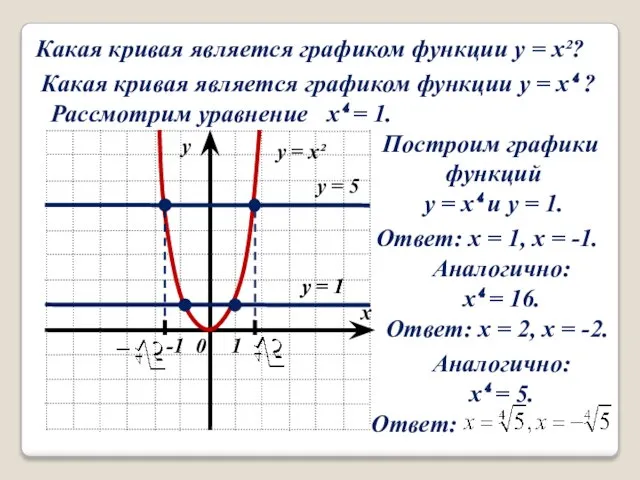
Какая кривая является графиком функции y = x²?
Какая кривая является графиком функции y = x⁴ ?
Рассмотрим уравнение x⁴ = 1.
Построим графики
функций
y = x⁴ и y = 1.
Ответ: x = 1, x = -1.
Аналогично:
x⁴ = 16.
Ответ: x = 2, x = -2.
Аналогично:
x⁴ = 5.
y = 5
Ответ:

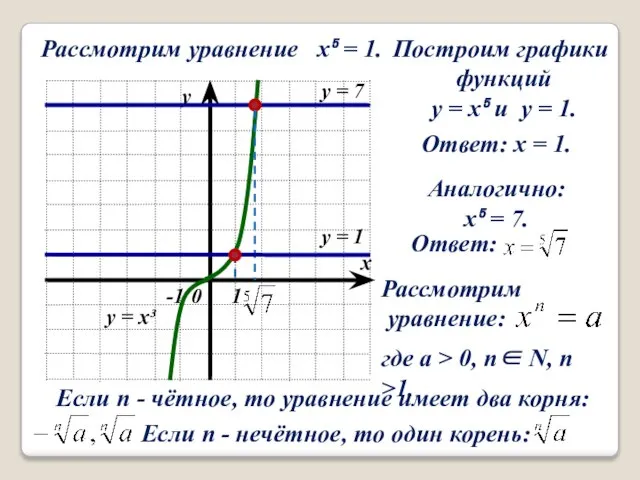
Рассмотрим уравнение x⁵ = 1.
Построим графики
функций
y = x⁵ и y = 1.
Аналогично:
x⁵ = 7.
Ответ: x = 1.
Ответ:
Рассмотрим
уравнение:
где a > 0, n N, n >1.
Если n - чётное, то уравнение имеет два корня:
Если n - нечётное, то один корень:

Определение 1 :
Корнем n – й степени из неотрицательного числа a
(n = 2,3,4,5,…) называют такое неотрицательное
число, которое при возведении в степень n даёт
в результате число a.
Это число обозначают:
a
n
- подкоренное выражение
-показатель корня
Операцию нахождения корня из неотрицательного
числа называют извлечением корня.

Операция извлечение корня является обратной
по отношению к возведению в соответствующую
степень.
5² = 25
10³ = 1000
0,3⁴ = 0,0081

Пример 1:
Вычислить: а)  49; б)  0,125; в)  0 ; г)  17
3
7
4
Решение:
а)  49 = 7, так как 7 > 0 и 7² = 49;
3
б)  0,125 = 0,5, так как 0,5 > 0 и 0,5³ = 0,125;
в)  0 ;
г)  17 ≈ 2,03
4
Определение 2 :
Корнем нечётной степени n из отрицательного
числа a (n = 3,5,…) называют такое
отрицательное число, которое при возведении
в степень n даёт в результате число a.

Итак
Вывод:
Корень чётной степени имеет смысл
(т.е. определён) только для неотрицательного
подкоренного выражения; корень нечётной степени
имеет смысл для любого подкоренного выражения.
Пример 2:
Решите уравнения:

Возведём обе части уравнения в куб:
а)
б)
Возведём обе части уравнения в четвёртую степень:
в)
Решений нет. Почему?
г)
Возведём обе части уравнения в шестую степень: