Одночлены и многочлены 7 класс

Устные упражнения.
Вычислите .
При некоторой паре (m,n) значений переменных m и n значение выражения m-n равно 2. Чему равно в этом случае значение выражения:
Представьте одночлен в виде произведения двух одночленов, один из которых равен:

Решение:
(1/8) · (16 – 8) = (1/8) · 8 = 1

Решение:
а) 2 · 2 = 4 ; б) 2 = 4 ; в) 2 = 8

Решение:
а) 6а b = 2а · 3b ;
б) 6а b = 2b · 3a ;
в) 6a b = 3a · 2a b ;
г) 6a b = ab · 18a b ;
д) 6a b = - 6 a b · (- ab ).

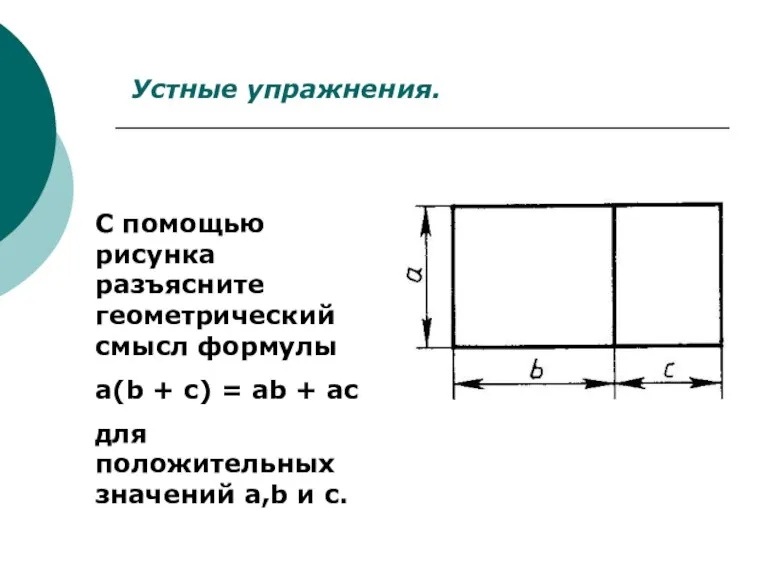
Устные упражнения.
С помощью рисунка разъясните геометрический смысл формулы
a(b + c) = ab + ac
для положительных значений a,b и с.

Устные упражнения.
Назовите и сформулируйте свойство, записанное с помощью формулы:
a(b + c) = ab + ac

Умножение многочлена на одночлен.
Рассмотрим прямоугольный параллелепипед, размеры которого указаны на рисунке, и найдём его объём.
V = длина × ширина × высота
Длина = 3а
Ширина = b
Высота = a + 2b + c

Применив распределительное свойство умножения, можно записать:
(a + 2b + c)·(3ab)=
= a · 3ab + 2b · 3ab + c · 3ab =
= 3a b + 6ab + 3abc