Содержание
- 2. Логика – наука, изучающая законы и формы мышления. Логика изучает: Формы мышления Способы мышления Логика (древнегреч.
- 3. История логики насчитывает около двух с половиной тысячелетий. Первые учения о формах и способах мышления возникли
- 4. Формальная логика ФОРМАЛЬНАЯ ЛОГИКА — наука о законах и формах правильного мышления.
- 5. Основные формы мышления Основными формами мышления являются: ПОНЯТИЯ, СУЖДЕНИЯ, УМОЗАКЛЮЧЕНИЯ. ПОНЯТИЕ - форма мышления, в которой
- 6. СУЖДЕНИЕ – это форма мышления, в которой что-либо утверждается или отрицается об объектах, их свойствах и
- 7. В дальнейшем своем развитии логика перешла от формальной к математической, появление которой связывают с именем Лейбница.
- 8. Основатель – немецкий ученый и философ Лейбниц(1642 -1716), предпринял попытку применения математических методов исследования Математическая логика
- 9. Алгебра логики – раздел математической логики, изучающий строение сложных логических высказываний и способы установления истинности с
- 10. Ток в цепи может либо протекать, либо отсутствовать, подобно тому, как утверждение может быть либо истинным,
- 11. ЛОГИКА ЛОГИКА — это наука о формах и законах человеческого мышления и, в частности, о законах
- 12. ФОРМЫ МЫШЛЕНИЯ Идеи и аппарат логики используется в кибернетике, вычислительной технике и электротехнике (построение компьютеров основано
- 13. Логические высказывания Логическое высказывание – это повествовательное предложение, относительно которого можно однозначно сказать, истинно оно или
- 14. Логические переменные Логические переменные – простые высказывания, содержащие только одну мысль. Обозначаются буквами латинского алфавита: A,
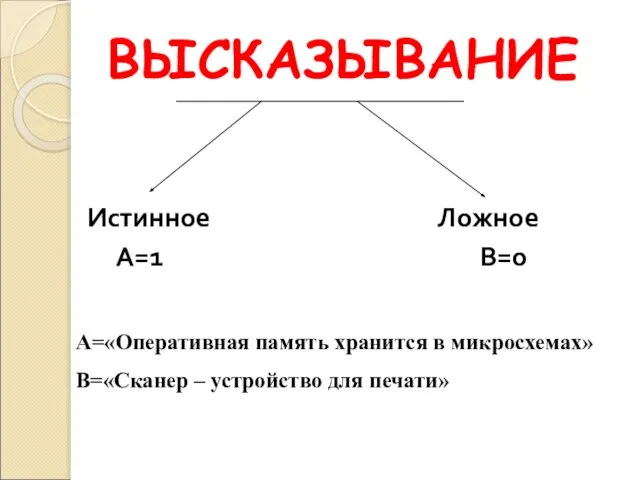
- 15. Истинное Ложное А=1 В=0 А=«Оперативная память хранится в микросхемах» В=«Сканер – устройство для печати» ВЫСКАЗЫВАНИЕ
- 16. Обозначение высказываний A – Сейчас идет дождь. B – Форточка открыта. простые высказывания (элементарные) Составные высказывания
- 17. Составные высказывания Высказывания, состоящие из нескольких простых суждений и содержащие в себе более, чем одну простую
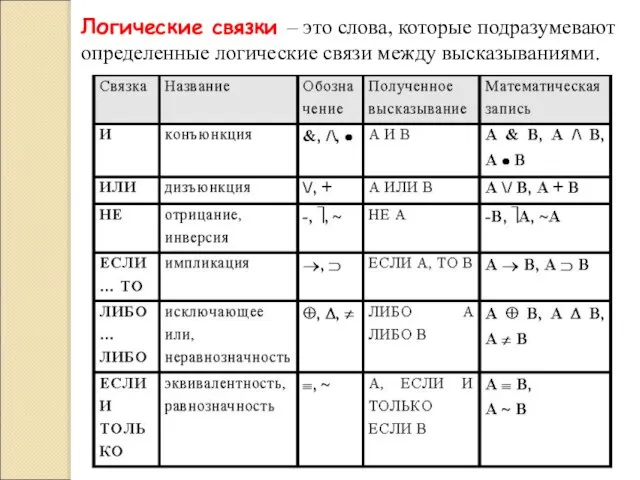
- 18. Логические связки – это слова, которые подразумевают определенные логические связи между высказываниями.
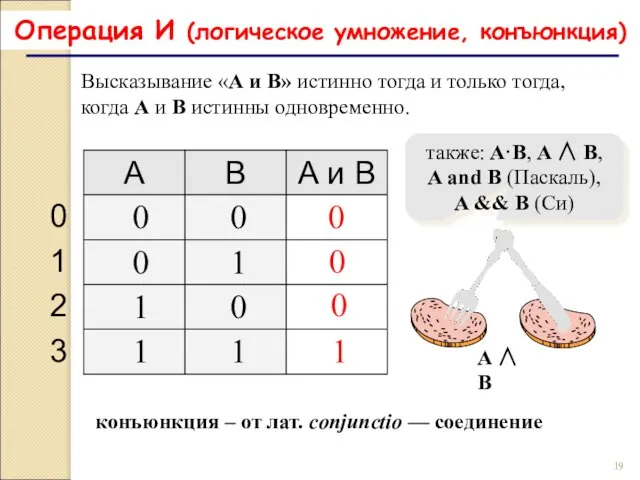
- 19. Операция И (логическое умножение, конъюнкция) 1 0 также: A·B, A ∧ B, A and B (Паскаль),
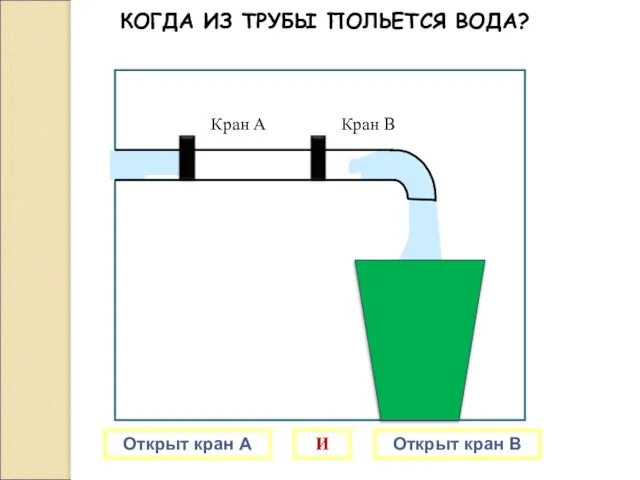
- 20. Кран В Кран А КОГДА ИЗ ТРУБЫ ПОЛЬЕТСЯ ВОДА? Открыт кран А Открыт кран В И
- 21. Значение логической функции определяется по ее таблице истинности Таблица истинности показывает какие значения принимает логическая функция
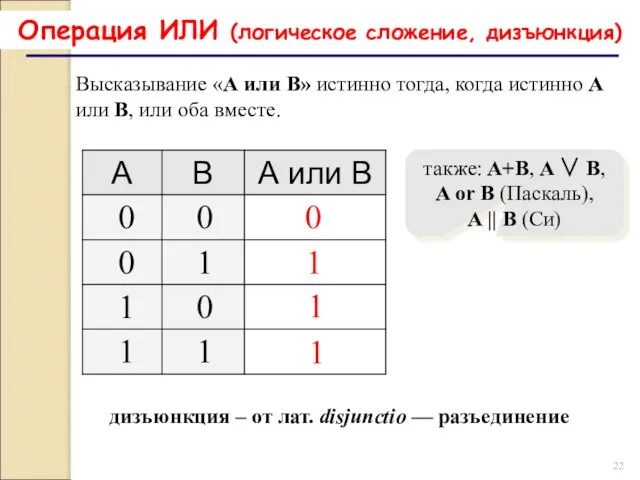
- 22. Операция ИЛИ (логическое сложение, дизъюнкция) 1 0 также: A+B, A ∨ B, A or B (Паскаль),
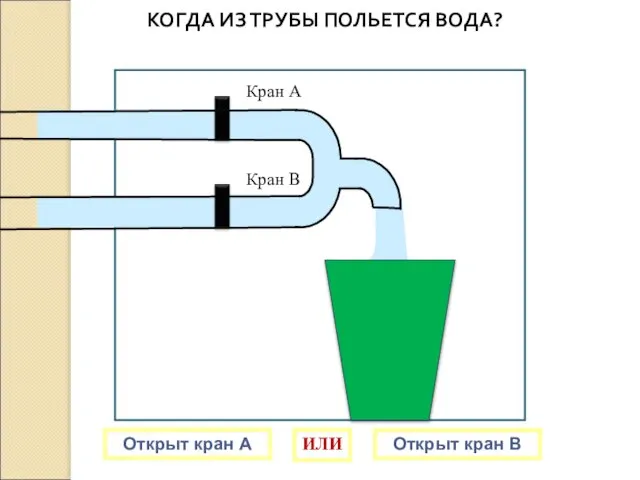
- 23. Кран А Кран В КОГДА ИЗ ТРУБЫ ПОЛЬЕТСЯ ВОДА? Открыт кран А Открыт кран В ИЛИ
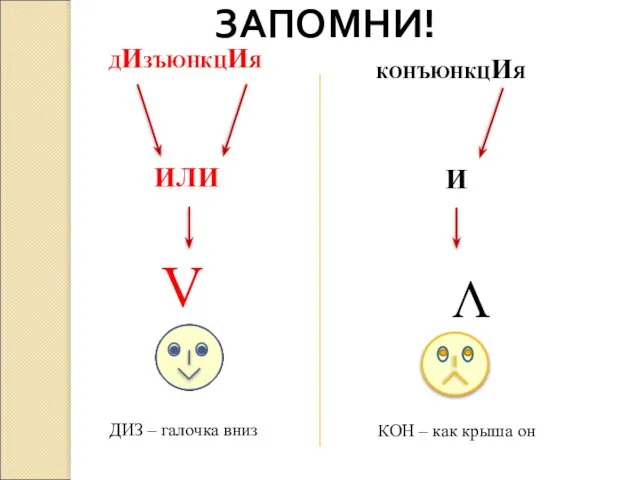
- 24. ЗАПОМНИ!
- 25. Логическое отрицание (инверсия) делает истинное высказывание ложным, а ложное – истинным [логическая отрицательная единица, перевертыш]
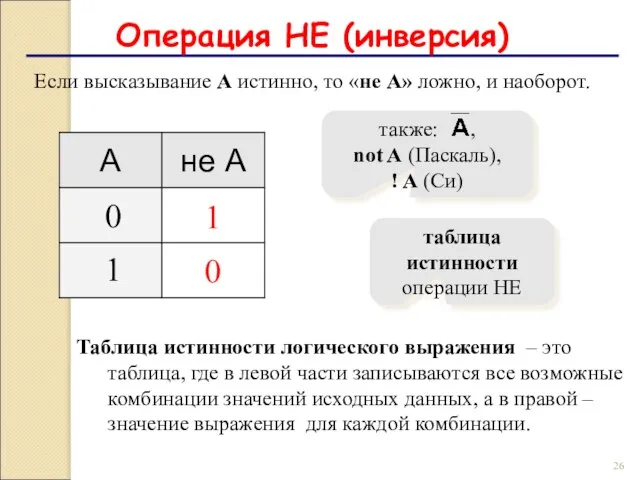
- 26. Операция НЕ (инверсия) Если высказывание A истинно, то «не А» ложно, и наоборот. 1 0 0
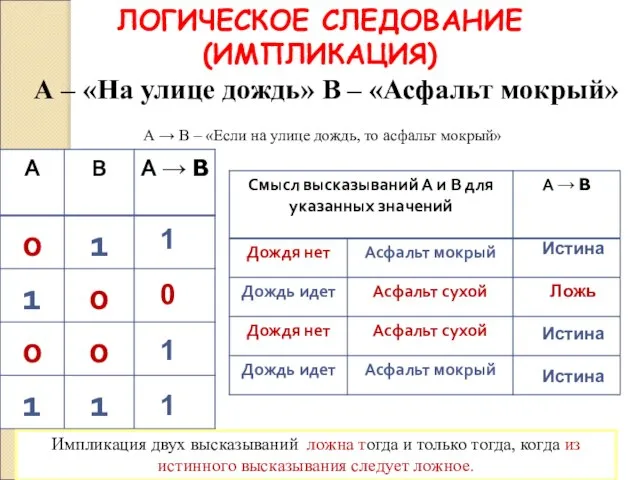
- 27. Импликация Объединение двух высказываний, из которых первое является условием, а второе – следствием из него, называется
- 28. Импликация («если …, то …») Высказывание «A → B» истинно, если не исключено, что из А
- 29. 1 0 1 1 Импликация двух высказываний ложна тогда и только тогда, когда из истинного высказывания
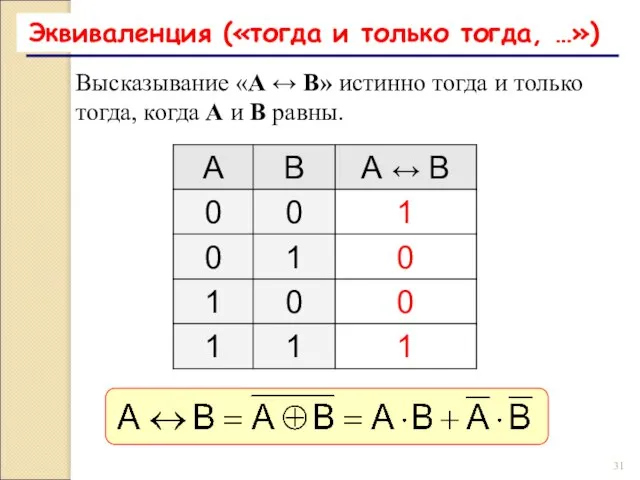
- 30. Эквиваленция Эквиваленция – это логическая операция, объединяющая два простых высказывания в одно составное и которое является
- 31. Эквиваленция («тогда и только тогда, …») Высказывание «A ↔ B» истинно тогда и только тогда, когда
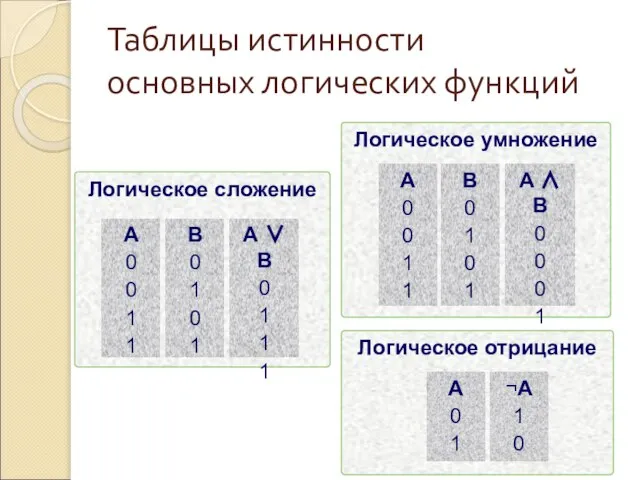
- 32. Таблицы истинности основных логических функций Логическое умножение A 0 0 1 1 B 0 1 0
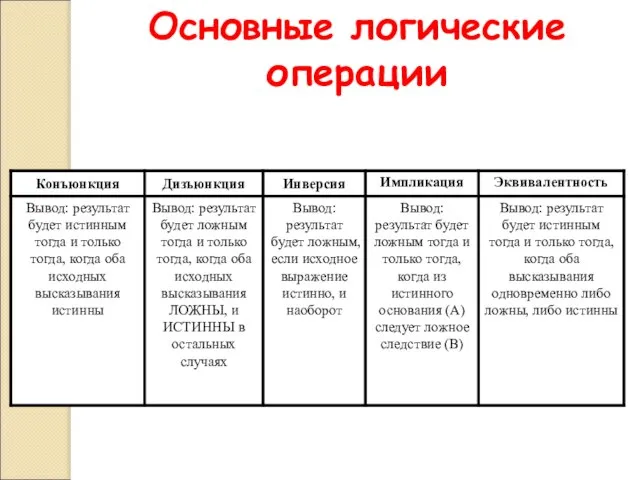
- 33. Основные логические операции
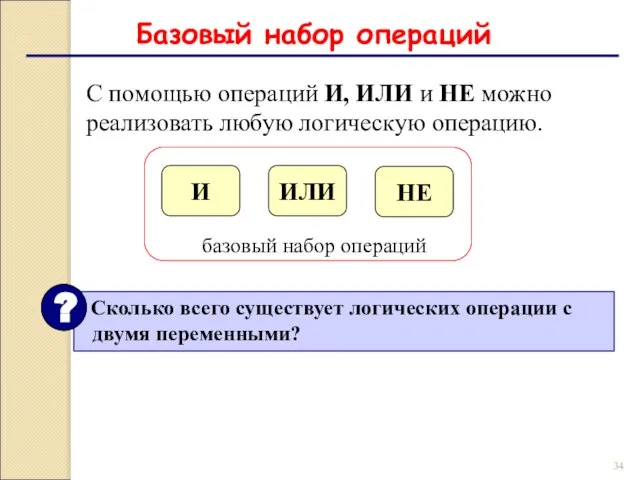
- 34. Базовый набор операций С помощью операций И, ИЛИ и НЕ можно реализовать любую логическую операцию.
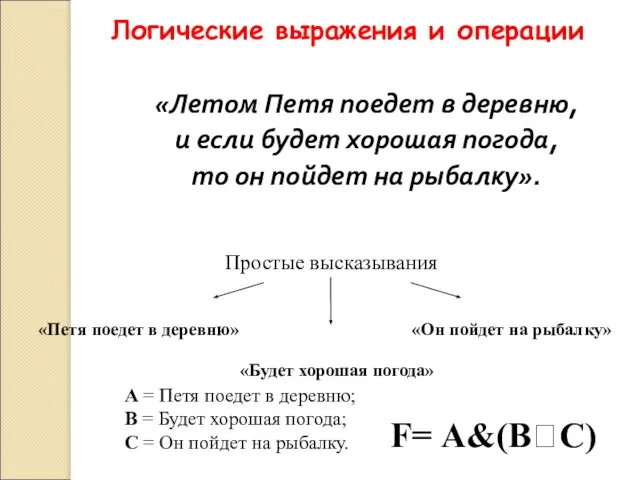
- 35. «Летом Петя поедет в деревню, и если будет хорошая погода, то он пойдет на рыбалку». Простые
- 37. Скачать презентацию
















![Логическое отрицание (инверсия) делает истинное высказывание ложным, а ложное – истинным [логическая отрицательная единица, перевертыш]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/874268/slide-24.jpg)



 Научные исследования
Научные исследования Гносеология как учение о познании
Гносеология как учение о познании Философия Древнего Востока
Философия Древнего Востока Проблема познания в философии
Проблема познания в философии Цитаты зарубежного и отечественного исследователя
Цитаты зарубежного и отечественного исследователя Философия науки (Тема 6)
Философия науки (Тема 6) Истина и ее критерии
Истина и ее критерии Становление наук о человеке. Гераклит
Становление наук о человеке. Гераклит Методологические основы научного знания
Методологические основы научного знания Наука и религия
Наука и религия Пять видов бессмертия в контексте современной жизни
Пять видов бессмертия в контексте современной жизни Воздействие техники на бытие человека и общества
Воздействие техники на бытие человека и общества Томмазо Кампанелла (1568-1639)
Томмазо Кампанелла (1568-1639)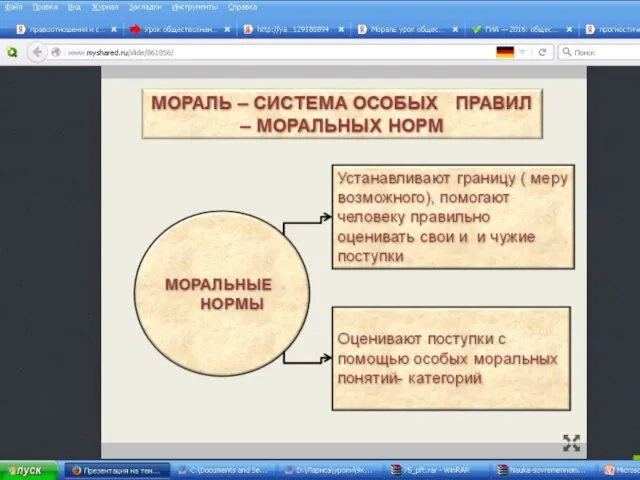 Мораль. Этика. Моральные нормы
Мораль. Этика. Моральные нормы Атеизм
Атеизм Культурно-исторический подход к проблеме развития мышления и речи человека (Леви-Брюль, Кеви-Стросс, Пиаже, Выготский)
Культурно-исторический подход к проблеме развития мышления и речи человека (Леви-Брюль, Кеви-Стросс, Пиаже, Выготский) История развитие йоги
История развитие йоги Психоанализ, как направление в современной философии
Психоанализ, как направление в современной философии Миссия и профессия
Миссия и профессия Классика Античной философии
Классика Античной философии неортодоксальные философские школы
неортодоксальные философские школы Мои размышления. Квантовая телепортация
Мои размышления. Квантовая телепортация Рациональность философии
Рациональность философии Философский пароход как историческое и интеллектуальное событие
Философский пароход как историческое и интеллектуальное событие Западноевропейская философская мысль в Новое время и эпоху Просвещения
Западноевропейская философская мысль в Новое время и эпоху Просвещения Джиотиша шастра
Джиотиша шастра Свобода, как условие самореализации личности
Свобода, как условие самореализации личности Istota ludzkiej pracy i jej sens
Istota ludzkiej pracy i jej sens