Слайд 2Key words:
Definition, equality, ordering, conjugate, addition and subtraction, multiplication, divison, modulus and

argument, Pythagoras' theorem, Euler.
Слайд 3Definition
A complex number is a number that can be expressed in
the form a + bi, where a and b are real numbers,

and i is a
solution of the equation x2 = −1. Because no real number
satisfies this equation, i is called an imaginary number.
For the complex number a + bi, a is called the real part,
and b is called the imaginary part. A complex number
can be visually represented as a pair of numbers (a, b)
forming a vector on a diagram called an Argand diagram,
representing the complex plane. "Re" is the real axis,
"Im" is the imaginary axis, and i satisfies i2 = −1.
Слайд 4For example, the equation
has no real solution, since the square of a

real number cannot be negative. Complex numbers provide a solution to this problem. The idea is to extend the real numbers with an indeterminate i (sometimes called the imaginary unit) that is taken to satisfy the relation i2 = −1, so that solutions to equations like the preceding one can be found. In this case the solutions are −1 + 3*i and −1 – 3*i, as can be verified using the fact that i2 = −1:
Слайд 5A complex number whose real part is zero is said to be

purely imaginary; the points for these numbers lie on the vertical axis of the complex plane. A complex number whose imaginary part is zero can be viewed as a real number; its point lies on the horizontal axis of the complex plane. Complex numbers can also be represented in polar form, which associates each complex number with its distance from the origin (its magnitude) and with a particular angle known as the argument of this complex number:
x+y*j=r*(cosθ+j *sinθ)
Слайд 6Some relations and operations
Equality.
Two complex numbers are equal if and only if both their

real and imaginary parts are equal. That is, complex numbers z1 and z2 are equal if and only if Re(z1) = Re(z2) and Im(z1) = Im(z2 )Nonzero complex numbers written in polar form are equal if and only if they have the same magnitude and their arguments differ by an integer multiple of 2π.
Слайд 7Ordering.
Since complex numbers are naturally thought of as existing on a two-dimensional

plane, there is no natural linear ordering on the set of complex numbers. In fact, there is no linear ordering on the complex numbers that is compatible with addition and multiplication – the complex numbers cannot have the structure of an ordered field. This is because any square in an ordered field is at least 0, but i2 = −1.
For example:
but:
Слайд 8Conjugate.
The complex conjugate of the complex number
z = x + y*i is given by x – y*i. It is denoted

by either
or z*. This unary operation on complex numbers cannot
be expressed by applying only their basic operations
addition, subtraction, multiplication and division.
Geometrically, is the reflection of z about the real axis.
Conjugating twice gives the original complex number,
which makes this operation an involution.
Слайд 9Addition and subtraction.
Two complex numbers a and b are most easily added by separately
adding their

real and imaginary parts of the summands. That is
to say:
Similarly, subtraction can be performed as
Слайд 10Multiplication.
Since the real part, the imaginary part, and the indeterminate i in a complex

number are all considered as numbers in themselves, two complex numbers, given as z = x + y*I and w = u + v*i are multiplied under the rules of the distributive property the commutative properties and the defining property i2 = -1 in the following way:
Слайд 11Divison.
Using the conjugation, the reciprocal of a nonzero complex number z = x + y*i can always be

broken down to
since nonzero implies that x2 + y2 is greater than zero.
This can be used to express a division of an arbitrary complex number w = u + v*i by a non-zero complex number z as
Слайд 12Modulus and argument
An alternative option for coordinates in the complex plane is

the polar coordinate system that uses the distance of the point z from the origin (O), and the angle subtended between the positive real axis and the line segment Oz in a counterclockwise sense. This leads to the polar form of complex numbers.
The absolute value (or modulus or magnitude) of a complex number z = x + y*i is
If z is a real number (that is, if y = 0), then r = |x|. That is, the absolute value of a real number equals its absolute value as a complex number.
Слайд 13Pythagoras' theorem
By Pythagoras' theorem, the absolute value of complex number is the

distance to the origin of the point representing the complex number in the complex plane.
In mathematics, the Pythagorean theorem, is a fundamental relation in Euclidean geometry among the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares on the other two sides. This theorem can be written as an equation relating the lengths of the sides a, b and c.
Слайд 14The argument of z (in many applications referred to as the "phase"

φ) is the angle of the radius Oz with the positive real axis, and is written as arg(z). As with the modulus, the argument can be found from the rectangular form x + y*i by applying the inverse tangent to the quotient of imaginary-by-real parts. By using a half-angle identity a single branch of the arctan suffices to cover the range of the arg-function, (−π, π], and avoids a more subtle case-by-case analysis
Слайд 15Normally, as given above, the principal value in the interval (−π, π]
![Normally, as given above, the principal value in the interval (−π, π]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/958276/slide-14.jpg)
is chosen. Values in the range [0, 2π) are obtained by adding 2π if the value is negative. The value of φ is expressed in radians. It can increase by any integer multiple of 2π and still give the same angle, viewed as subtended by the rays of the positive real axis and from the origin through z. Hence, the arg function is sometimes considered as multivalued. The polar angle for the complex number 0 is indeterminate, but arbitrary choice of the polar angle 0 is common.
The value of φ equals the result of atan2:
Слайд 16Together, r and φ give another way of representing complex numbers, the

polar form, as the combination of modulus and argument fully specify the position of a point on the plane. Recovering the original rectangular coordinates from the polar form is done by the formula called trigonometric form
Using Euler's formula this can be written as













![Normally, as given above, the principal value in the interval (−π, π]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/958276/slide-14.jpg)

 Презентация на тему Модели атома
Презентация на тему Модели атома  Работа и потенциал электростатического поля. Лекция 2
Работа и потенциал электростатического поля. Лекция 2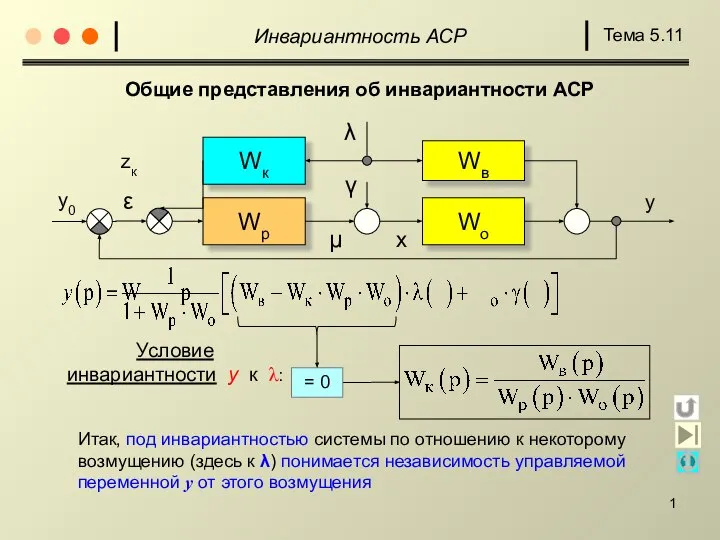 Инвариантность АСР
Инвариантность АСР Презентация на тему Электрические явления 9 класс
Презентация на тему Электрические явления 9 класс  Механика. Лекция 6. Момент инерции. Уравнение моментов
Механика. Лекция 6. Момент инерции. Уравнение моментов Электромагнитная индукция
Электромагнитная индукция Двигатели технический систем
Двигатели технический систем Электронно-дырочный переход (p-n-переход)
Электронно-дырочный переход (p-n-переход) Статистическое моделирование рисков продажи запасных частей
Статистическое моделирование рисков продажи запасных частей Компенсация реактивной мощности
Компенсация реактивной мощности Установка батарей своими руками
Установка батарей своими руками Особенности плавания в условиях ограниченной видимости на участке поселок Шиморское- поселок Елатьма
Особенности плавания в условиях ограниченной видимости на участке поселок Шиморское- поселок Елатьма Разветвленная цепь синусоидального тока
Разветвленная цепь синусоидального тока Реактивное движение
Реактивное движение Естественный способ задания движения
Естественный способ задания движения Электрический ток в электролитах. Электрическая диссоциация
Электрический ток в электролитах. Электрическая диссоциация Пузырьковая камера
Пузырьковая камера Топографическое представление местности при проектировании железных дорог
Топографическое представление местности при проектировании железных дорог Атомная энергетика
Атомная энергетика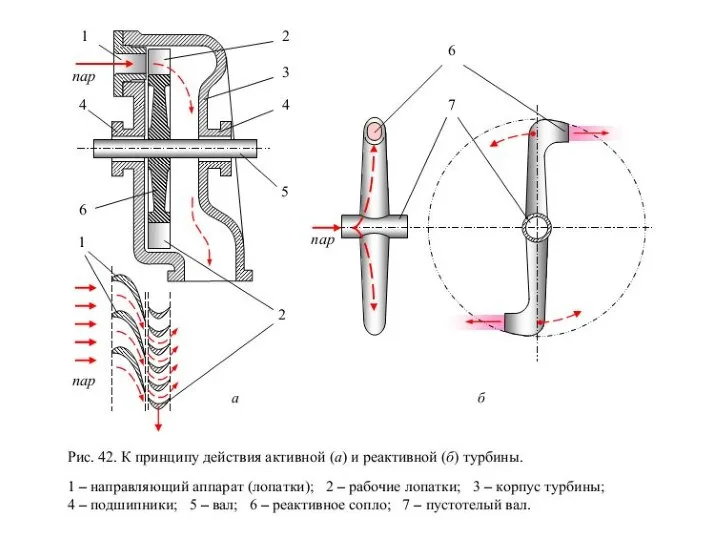 Теория турбин (заочники)
Теория турбин (заочники) Вечный двигатель в истории
Вечный двигатель в истории Методы определения и единицы измерения влажности воздуха
Методы определения и единицы измерения влажности воздуха Ответ на билет № 24 по физике (7 класс)
Ответ на билет № 24 по физике (7 класс) Электростатика. Связь напряженности и потенциала электрического поля
Электростатика. Связь напряженности и потенциала электрического поля Интерференция света
Интерференция света Двойные интегралы
Двойные интегралы Презентация на тему Электроизмерительные приборы
Презентация на тему Электроизмерительные приборы  Магнитное поле
Магнитное поле