Содержание
- 2. Физическая оптика Для описания разрешающей способности прибора геометрической оптики недостаточно. В качестве следующей аппроксимации используется физическая
- 3. Допущения физической оптики Длина волны света конечна. Распространение света есть распространение электромагнитных колебаний в виде волновых
- 4. Интерференция волн Интерференция волновых фронтов от двух одинаковых источников приводит к образованию псевдо-структур - пучностей и
- 5. Когерентный свет Световые волны (одинаковой длины волны), которые приходят в данную точку с постоянной (не изменяющейся
- 6. Источники света и интерференция Лазерный пучок высококогерентен (длина когерентного цуга составляет от 20 см до 100
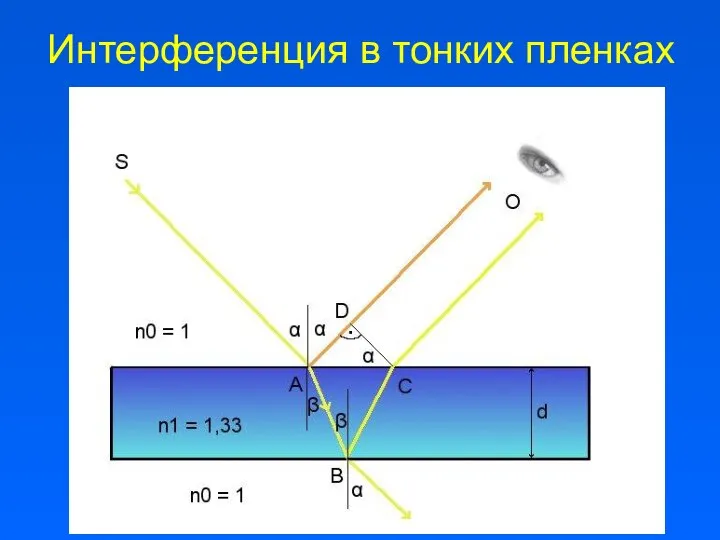
- 7. Интерференция в тонких пленках
- 8. Кольца Ньютона – интерференция в тонком слое Картина колец Ньютона постоянна во времени из-за минимального сдвига
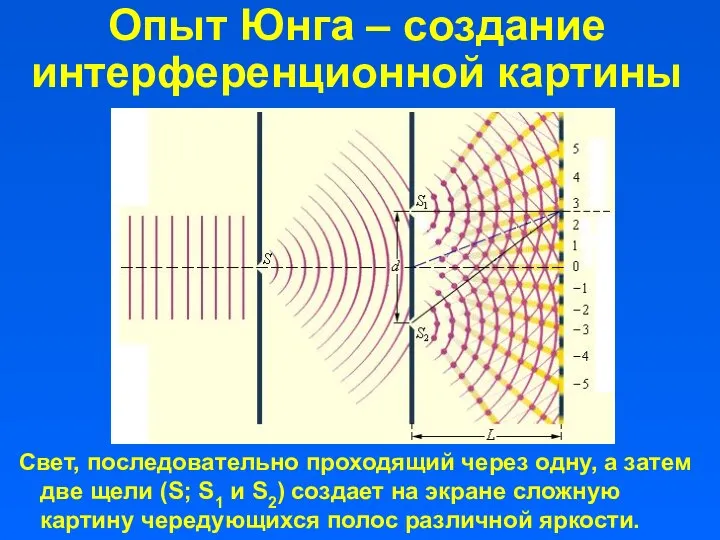
- 9. Опыт Юнга – создание интерференционной картины Свет, последовательно проходящий через одну, а затем две щели (S;
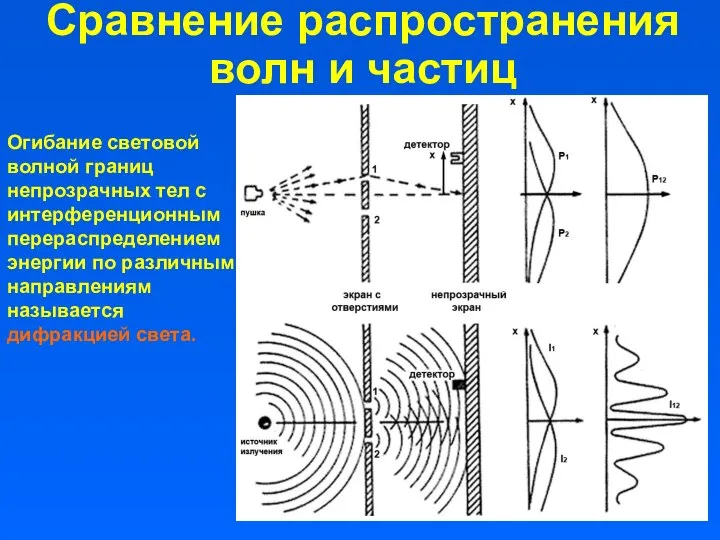
- 10. Сравнение распространения волн и частиц Огибание световой волной границ непрозрачных тел с интерференционным перераспределением энергии по
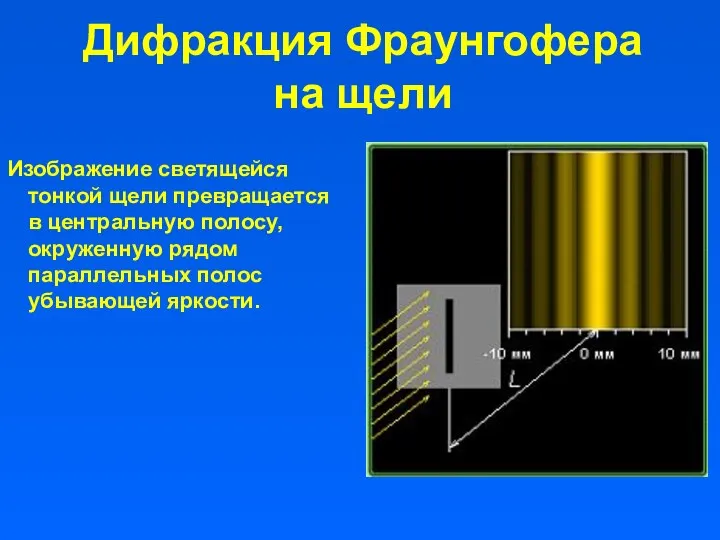
- 11. Дифракция Фраунгофера на щели Изображение светящейся тонкой щели превращается в центральную полосу, окруженную рядом параллельных полос
- 12. Дифракция Фраунгофера на малом круглом отверстии Изображение светящейся точки превращается в центральное пятно, окруженное рядом концентрических
- 13. Диск Эри – изображение точечного объекта идеальной линзой
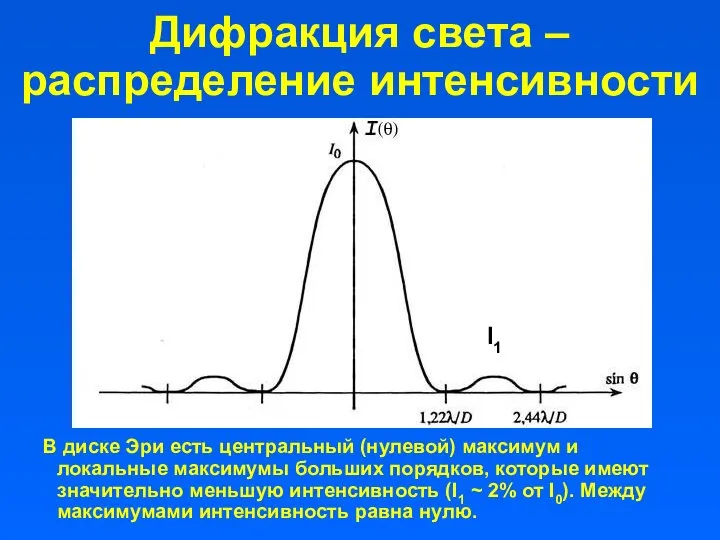
- 14. Дифракция света – распределение интенсивности В диске Эри есть центральный (нулевой) максимум и локальные максимумы больших
- 15. Полное распределение интенсивности в диске Эри описывается формулой: где I(θ) – интенсивность, k=2π/λ есть волновое число,
- 16. Поскольку величина первого максимума в диске Эри составляет менее 2% от нулевого, им и последующими максимумами
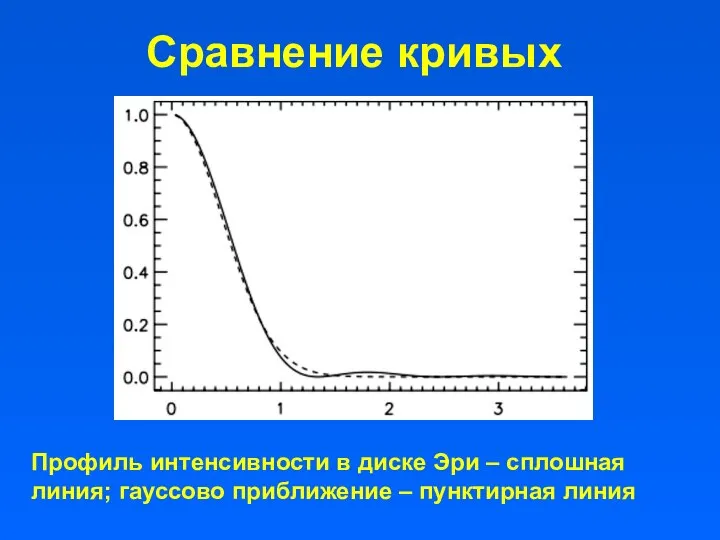
- 17. Сравнение кривых Профиль интенсивности в диске Эри – сплошная линия; гауссово приближение – пунктирная линия
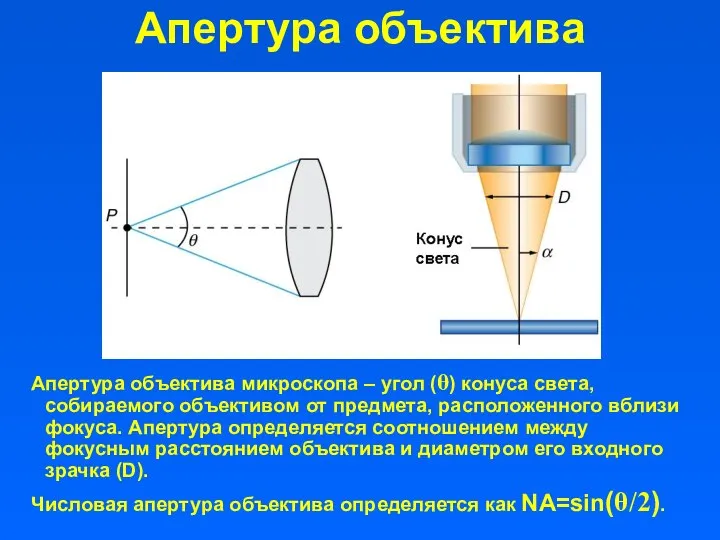
- 18. Апертура объектива Апертура объектива микроскопа – угол (θ) конуса света, собираемого объективом от предмета, расположенного вблизи
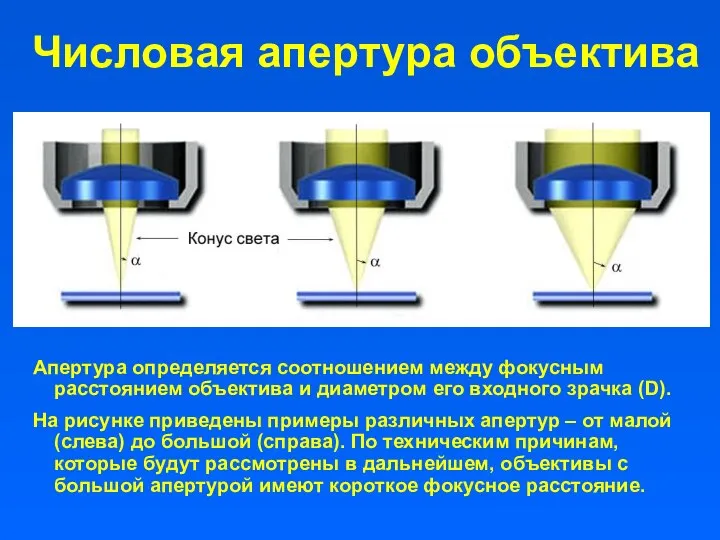
- 19. Числовая апертура объектива Апертура определяется соотношением между фокусным расстоянием объектива и диаметром его входного зрачка (D).
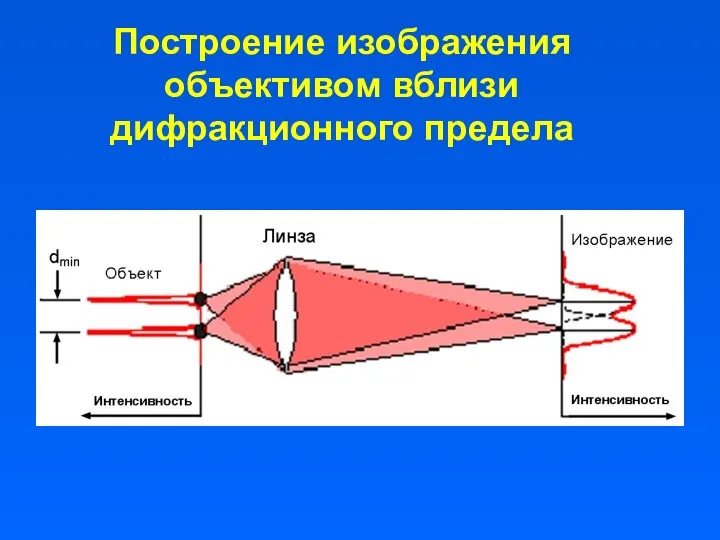
- 20. Построение изображения объективом вблизи дифракционного предела
- 21. Критерий Рэлея Поскольку изображение светящейся точки представляет собой светящийся диск Эри, то разрешение определяется расстоянием между
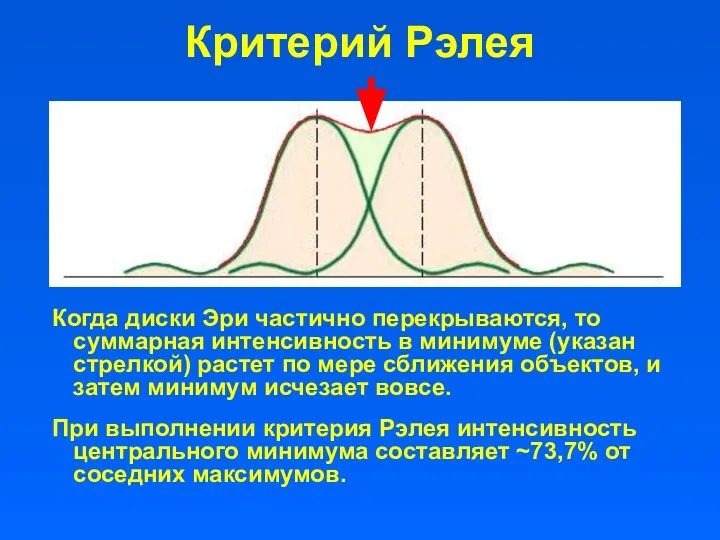
- 22. Критерий Рэлея Когда диски Эри частично перекрываются, то суммарная интенсивность в минимуме (указан стрелкой) растет по
- 23. Изображения точек идеальной линзой Слева – размер диска Эри (радиус первого минимума) определяется апертурой объектива (апертура
- 24. Дифракционная решетка Дифракционная решетка – система параллельных (прозрачных) щелей, разделенных непрозрачным промежутком, ширина которого примерно равна
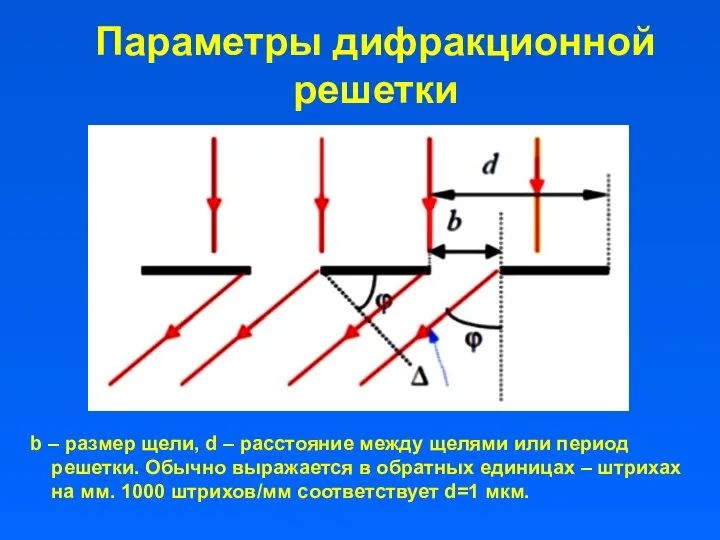
- 25. Параметры дифракционной решетки b – размер щели, d – расстояние между щелями или период решетки. Обычно
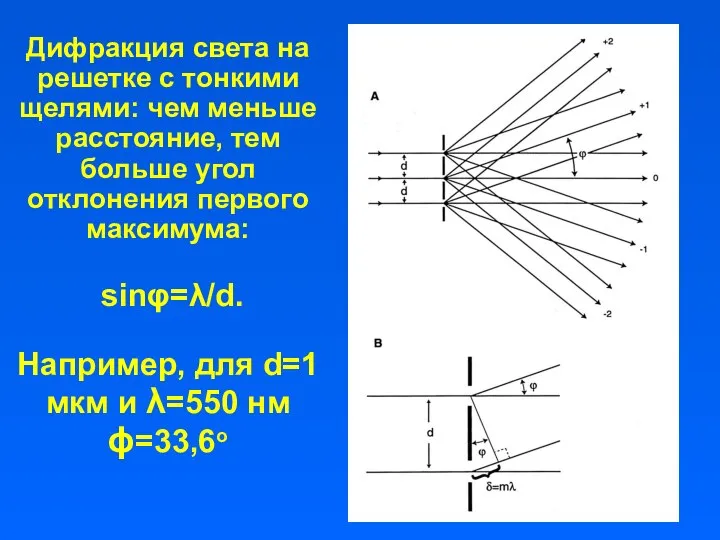
- 26. Дифракция света на решетке с тонкими щелями: чем меньше расстояние, тем больше угол отклонения первого максимума:
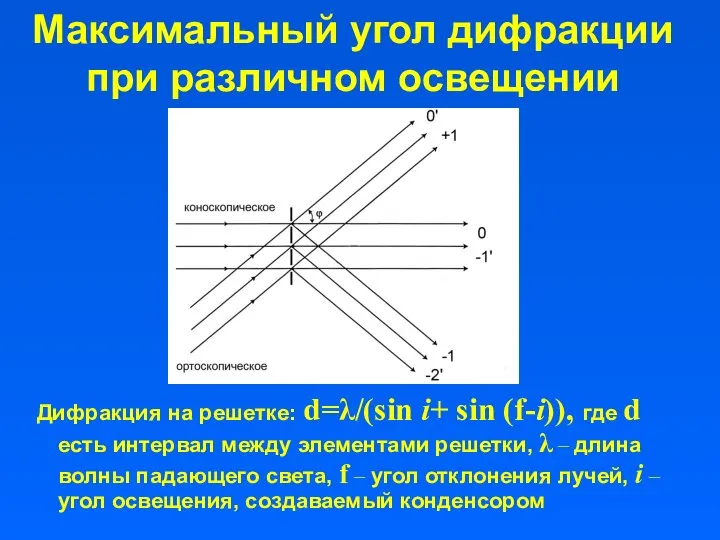
- 27. Максимальный угол дифракции при различном освещении Дифракция на решетке: d=λ/(sin i+ sin (f-i)), где d есть
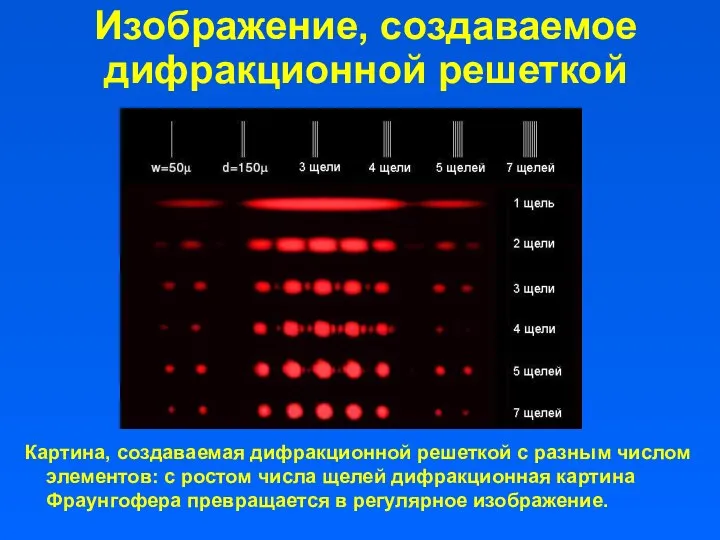
- 28. Изображение, создаваемое дифракционной решеткой Картина, создаваемая дифракционной решеткой с разным числом элементов: с ростом числа щелей
- 29. Дифракционная картина в з.ф.п. – решетка с разными периодами Расстояние между максимумами в з.ф.п. объектива растет
- 30. Решетка и маски для наблюдения эффектов Аббе Препарат представлял собой набор небольших решеток с разным шагом
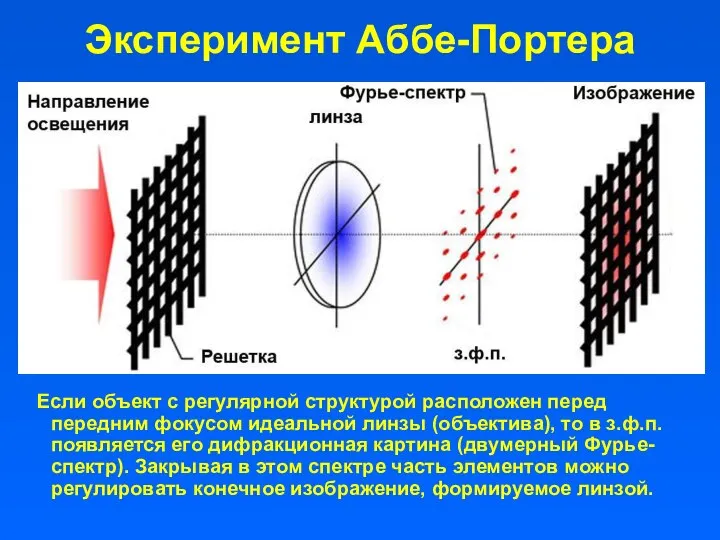
- 31. Эксперимент Аббе-Портера Если объект с регулярной структурой расположен перед передним фокусом идеальной линзы (объектива), то в
- 32. Эксперименты Аббе 1. Изображение решетки не меняется, если закрыть большую часть задней фокальной плоскости объектива, но
- 33. Влияние закрытия дифрационных максимумов на вид решетки
- 34. Фурье-образ решетки в з.ф.п. объектива Если перекрыть промежуточные максимумы в з.ф.п. объектива, то плотность штрихов в
- 35. Теория Аббе Изображение в микроскопе формируется в результате интерференции прямого и дифрагированного света в задней фокальной
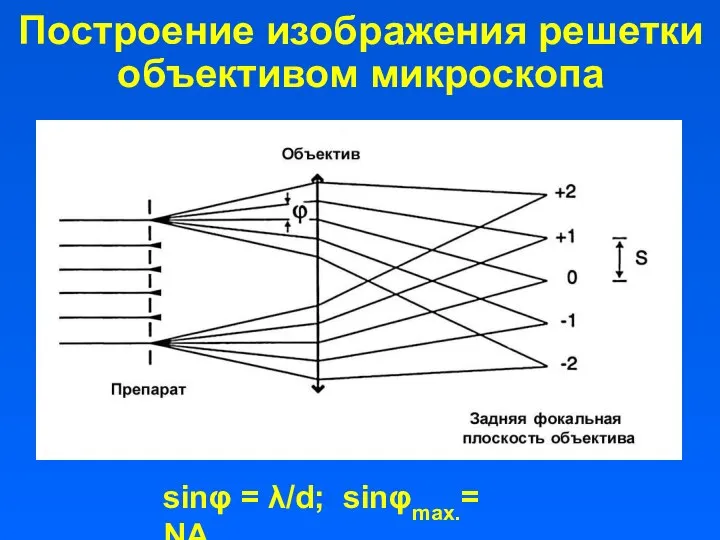
- 36. Построение изображения решетки объективом микроскопа sinφ = λ/d; sinφmax.= NАоб.
- 37. Разрешающая способность микроскопа по Аббе Для дифракционной решетки угол первого дифракционного максимума α рассчитывается по формуле:
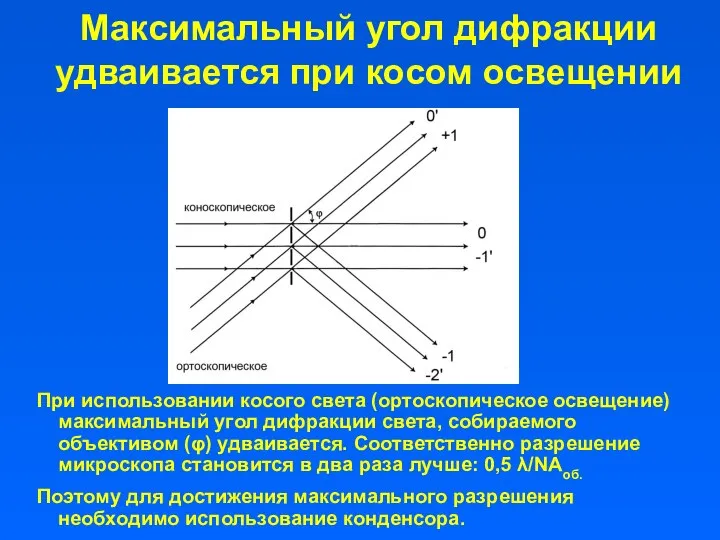
- 38. Максимальный угол дифракции удваивается при косом освещении При использовании косого света (ортоскопическое освещение) максимальный угол дифракции
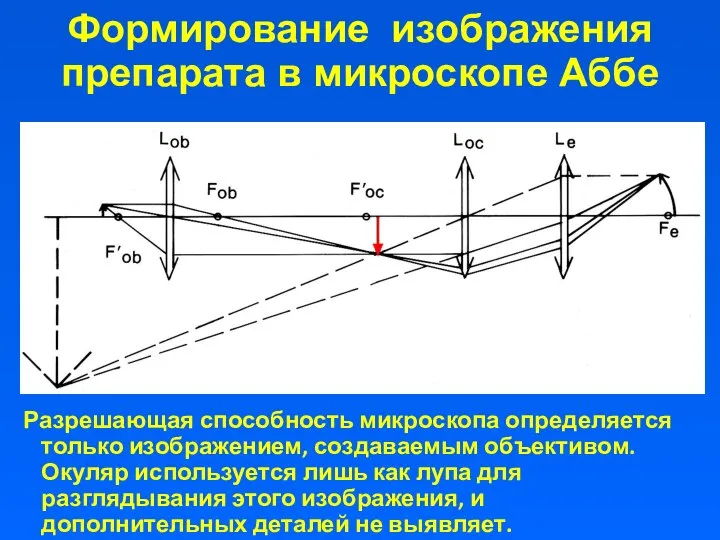
- 39. Формирование изображения препарата в микроскопе Аббе Разрешающая способность микроскопа определяется только изображением, создаваемым объективом. Окуляр используется
- 40. Разрешающая способность объектива микроскопа Согласно критерию Рэлея, разрешение свободного от аберраций оптического прибора может быть вычислено
- 42. Скачать презентацию





















 Основные положения молекулярно-кинетической теории
Основные положения молекулярно-кинетической теории Устройство микросамолёта R-20 Птенец-2
Устройство микросамолёта R-20 Птенец-2 Материаловедениие. Классификация материалов по функциям
Материаловедениие. Классификация материалов по функциям Свободное падение тел. Динамика материальной точки
Свободное падение тел. Динамика материальной точки Фазовая автоподстройка (ФАП) в приемниках ОФМн радиосигналов. Схемы Пистолькорса и Сифорова
Фазовая автоподстройка (ФАП) в приемниках ОФМн радиосигналов. Схемы Пистолькорса и Сифорова Магнитное поле
Магнитное поле Электрический ток. Источники тока
Электрический ток. Источники тока Уравнение Бернулли. Лекция №4
Уравнение Бернулли. Лекция №4 Диэлектрики в электростатическом поле
Диэлектрики в электростатическом поле Логарифмическая шкала децибелов
Логарифмическая шкала децибелов Вариант расчета ФР. Закон смещения Вина
Вариант расчета ФР. Закон смещения Вина Механические колебания. Тест
Механические колебания. Тест Из чего состоит велосипед
Из чего состоит велосипед Молекулярная физика и термодинамика. Тест
Молекулярная физика и термодинамика. Тест Действие магнитного поля на движущийся заряд. Сила Лоренца
Действие магнитного поля на движущийся заряд. Сила Лоренца Презентация на тему Механические свойства твердых тел
Презентация на тему Механические свойства твердых тел  Механическое движение
Механическое движение Физика пластической деформации кристаллов
Физика пластической деформации кристаллов Последовательное соединение проводников
Последовательное соединение проводников Давление газа
Давление газа Электрические явления
Электрические явления Электрический ток в вакууме
Электрический ток в вакууме Видимый свет
Видимый свет Презентация на тему Закон всемирного тяготения. Движение планет
Презентация на тему Закон всемирного тяготения. Движение планет  10 плавление
10 плавление МКТ строения вещества
МКТ строения вещества Презентация на тему Из чего состоит вода?
Презентация на тему Из чего состоит вода?  Всемирное тяготение
Всемирное тяготение