Содержание
- 2. Термин "модель" широко используется в различных сферах человеческой деятельности и имеет множество смысловых значений. Под "моделью"
- 3. Моделирование - процесс построения, изучения и применения моделей, иначе говоря, моделирование - это изучение объектa путем
- 4. Основная задача математического моделирования – выделение законов в природе, обществе и технике и запись их на
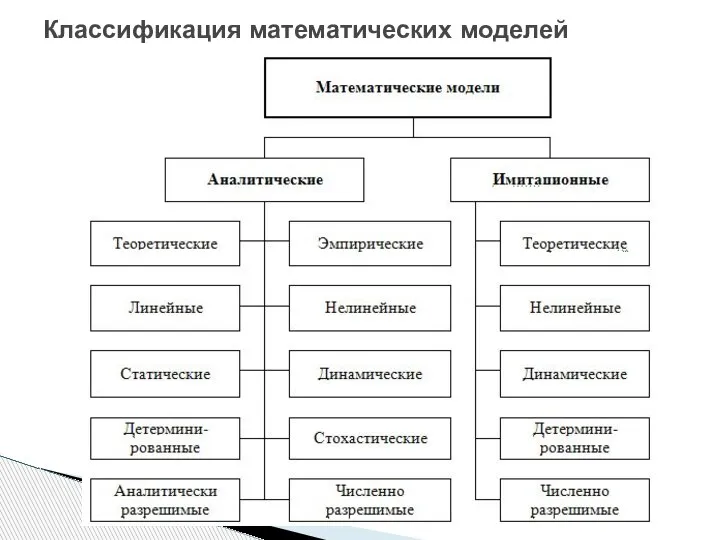
- 5. Классификация математических моделей
- 6. Классификация математических моделей Все математические модели по использованному формальному языку можно разбить на аналитические и имитационные.
- 7. Классификация математических моделей Аналитические модели в свою очередь разбиваются на теоретические и эмпирические модели. Теоретические модели
- 8. Геометрическое представление математических моделей Геометрически математическая модель может быть представлена как некоторая поверхность отклика, соответствующая расположению
- 9. Основные этапы математического моделирования 1) Построение модели. На этом этапе задается некоторый «нематематический» объект — явление
- 10. Основные этапы математического моделирования 3) Интерпретация полученных следствий из математической модели. Следствия, выведенные из модели на
- 11. Математические модели аналитического типа Простейшие аналитические модели могут быть заданы явно в виде функции одной или
- 12. Математические модели аналитического типа Модель, заданная в явном виде, дает исчерпывающее описание исследуемого объекта. Она позволяет
- 13. Линейные математические модели Наиболее простыми являются так называемые линейные детерминированные модели. Они задаются в виде линейной
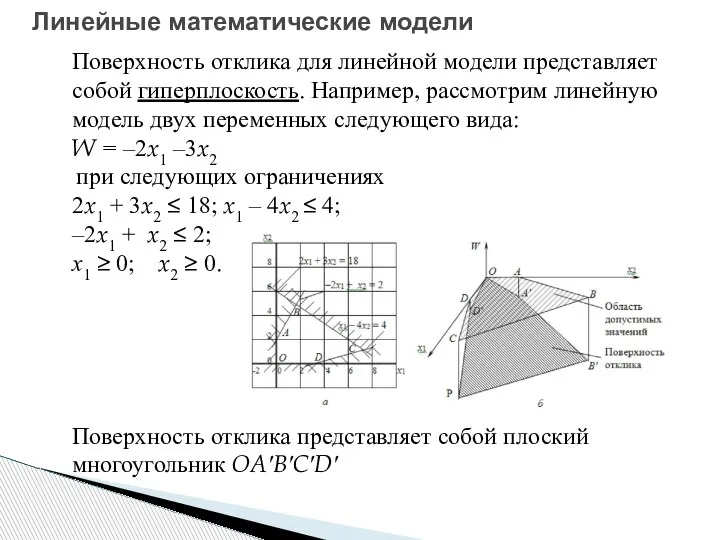
- 14. Линейные математические модели Поверхность отклика для линейной модели представляет собой гиперплоскость. Например, рассмотрим линейную модель двух
- 15. Линейные математические модели Примером такой модели является классическая модель стоимости перевозок (транспортная задача). Имеется k пунктов
- 16. Линейные математические модели Количество продукта, перевозимого из i-го пункта производства в j-й пункт потребления, равно xij;
- 17. Линейные математические модели Линейное дифференциальное уравнение в частных производных имеет вид. Модель, заданная в виде дифференциального
- 18. Нелинейные детерминированные модели Нелинейные детерминированные модели обладают бóльшей точностью и гибкостью. Они могут быть заданы в
- 19. Нелинейные детерминированные модели Нелинейные модели могут быть записаны в виде функционала, зависящего от управляющих переменных х
- 20. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ В ВИДЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ Математическая модель в виде одного или нескольких обыкновенных дифференциальных
- 21. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ В ВИДЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ Модель, заданная в виде дифференциальных уравнений, должна включать в
- 22. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ В ВИДЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В качестве простейшего примера математической модели механической системы может
- 23. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ В ВИДЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ Согласно принципу Даламбера сумма всех сил, действующих на груз
- 24. Модели, заданные в виде уравнений в частных производных Ряд задач, связанных с использованием физических полей, приводит
- 25. Модели, заданные в виде уравнений в частных производных Линейное дифференциальное уравнение в частных производных имеет вид
- 26. Стохастические модели Точные величины и зависимости, используемые в детерминированных моделях, представляют собой лишь некоторые средние значения
- 27. ЭМПИРИЧЕСКИЕ МАТЕМАТИЧЕСКИЕ МОДЕЛИ При разработке эмпирической математической модели предполагается использование экспериментальных данных, полученных при испытаниях объектов.
- 28. ЭМПИРИЧЕСКИЕ МАТЕМАТИЧЕСКИЕ МОДЕЛИ Объект идентификации представляет собой так называемый «черный ящик» с некоторым числом регулируемых (или,
- 29. ЭМПИРИЧЕСКИЕ МАТЕМАТИЧЕСКИЕ МОДЕЛИ Задачей идентификации является построение модели объекта по результатам наблюдений его реакции на возмущения
- 30. ЭМПИРИЧЕСКИЕ МАТЕМАТИЧЕСКИЕ МОДЕЛИ При этом на практике может встретиться два случая: 1) Форма математической модели известна
- 31. ЭМПИРИЧЕСКИЕ МАТЕМАТИЧЕСКИЕ МОДЕЛИ Конкретный вид модели зависит от выбора функций fq(x), по которым производится разложение W.
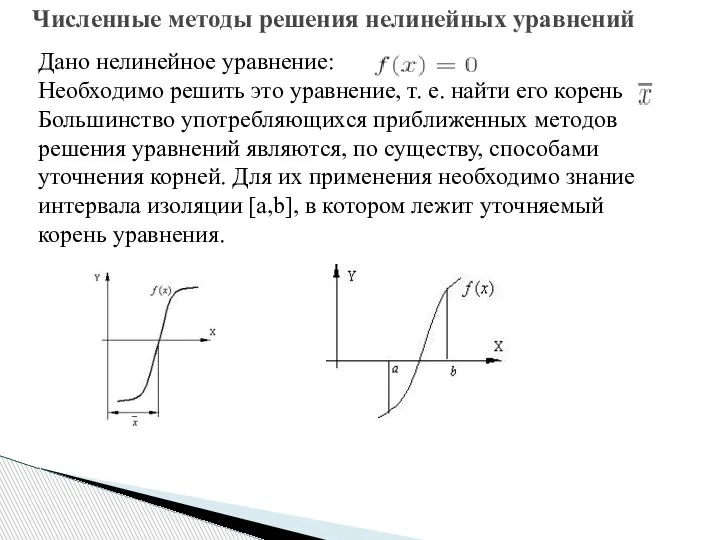
- 32. Численные методы решения нелинейных уравнений Дано нелинейное уравнение: Необходимо решить это уравнение, т. е. найти его
- 33. Численные методы решения нелинейных уравнений Процесс определения корней алгебраических и трансцендентных уравнений состоит из 2 этапов:
- 34. Численные методы решения нелинейных уравнений Процесс определения интервала изоляции [a,b], содержащего только один из корней уравнения,
- 35. Численные методы решения нелинейных уравнений На первом этапе, как правило, применяется графический метод исследования функции f(x),
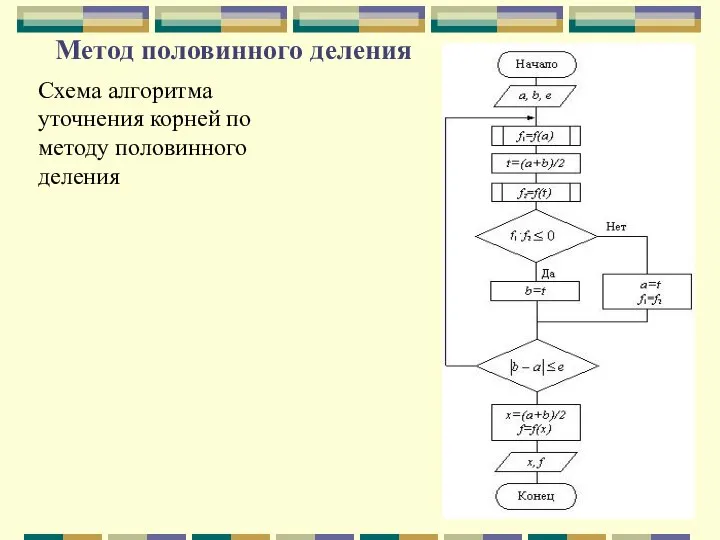
- 36. Метод половинного деления Дано нелинейное уравнение f(x)=0. Найти корень уравнения, принадлежащий отрезку [a,b], с заданной точностью
- 37. Метод половинного деления Для этого: 1) Вычисляем значение функции f(x) в точках a и t. 2)
- 38. Метод половинного деления Схема алгоритма уточнения корней по методу половинного деления
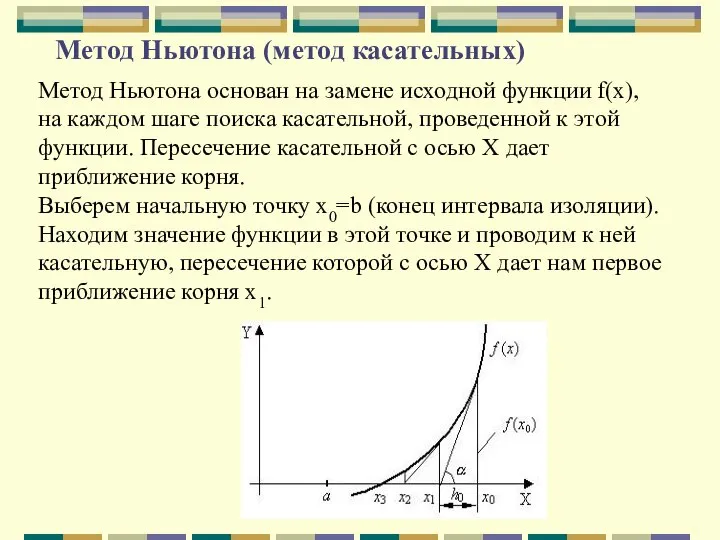
- 39. Метод Ньютона (метод касательных) Метод Ньютона основан на замене исходной функции f(x), на каждом шаге поиска
- 40. Метод Ньютона (метод касательных) В результате итерационный процесс схождения к корню реализуется рекуррентной формулой Процесс поиска
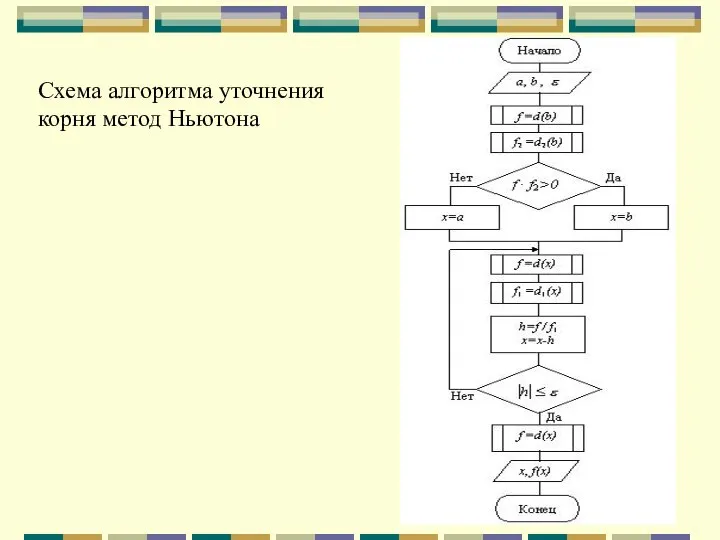
- 41. Схема алгоритма уточнения корня метод Ньютона
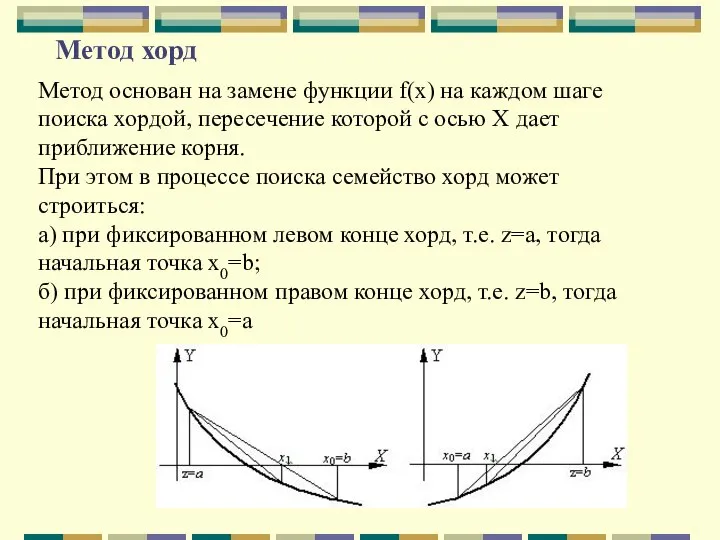
- 42. Метод хорд Метод основан на замене функции f(x) на каждом шаге поиска хордой, пересечение которой с
- 43. Метод хорд В результате итерационный процесс схождения к корню реализуется рекуррентной формулой: для случая а) для
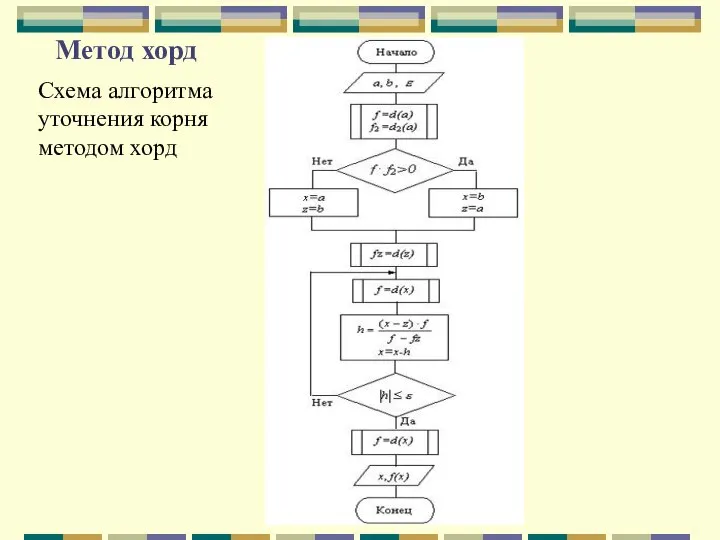
- 44. Метод хорд Схема алгоритма уточнения корня методом хорд
- 45. Решение систем линейных уравнений (СЛАУ) Постановка задачи Требуется найти решение системы n линейных уравнений: a11·x1 +a12·x2+…+a1n·xn=b1
- 46. Решение систем линейных уравнений (СЛАУ) Необходимым и достаточным условием существования единственного решения СЛАУ является условие det
- 47. Решение систем линейных уравнений (СЛАУ) Описание метода простой итерации Из первого уравнения системы a11·x1 +a12·x2+…+a1n·xn=b1 a21·x1
- 48. Метод простой итерации Подставим в правую часть этой системы значения и получим . Первая итерация закончена
- 50. Итерационный процесс в методе Гаусса-Зейделя строится по формуле после выбора соответствующего начального приближения . Метод Гаусса-Зейделя
- 51. Таким образом, i-тая компонента (k+1) -го приближения вычисляется по формуле: Условие сходимости Приведём достаточное условие сходимости
- 52. Условие окончания Условие окончания итерационного процесса Зейделя при достижении точности в упрощённой форме имеет вид: Более
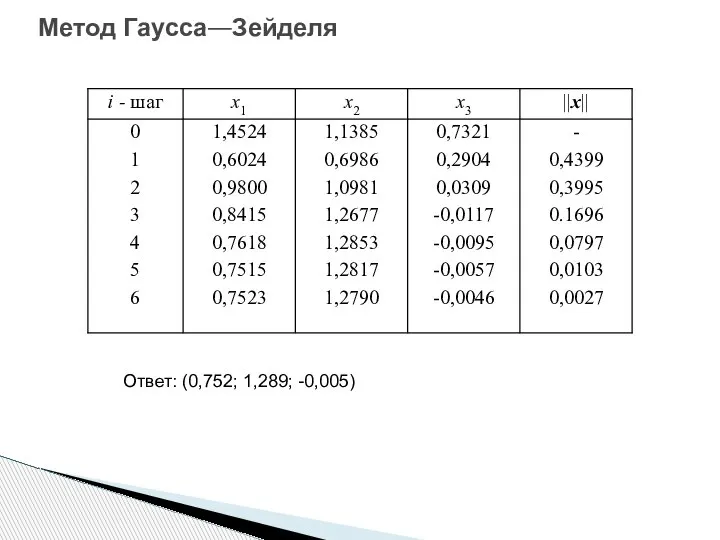
- 53. Пример. Методом Зейделя решить систему (точность 0,01) Приведем систему к виду Метод Гаусса—Зейделя
- 54. Метод Гаусса—Зейделя Ответ: (0,752; 1,289; -0,005)
- 55. Одной из важнейших задач численного анализа является задача интерполяции функции: требуется восстановить функцию f(x) для всех
- 56. Пусть известные значения некоторой функции f образуют следующую таблицу: При этом требуется получить значение функции f
- 57. Задача интерполирования может иметь в общей постановке бесчисленное множество решений или совсем их не иметь. Однако
- 58. Интерполяционный многочлен должен пройти через каждую узловую точку (xi, yi) таблицы, т.е., Подставляя каждую узловую точку
- 59. Интерполяционный многочлен может быть построен при помощи специальных интерполяционных формул Лагранжа, Ньютона, Стерлинга, Бесселя и др.
- 60. Докажем, что многочлен Лагранжа является интерполяционным многочленом, проходящим через все узловые точки, т.е. в узлах интерполирования
- 61. Таким образом, интерполяционный многочлен Лагранжа приближает заданную табличную функцию, т.е. Ln(xi) = yi и мы можем
- 62. Пример. N=1 (два узла интерполяции) уравнение прямой, проходящей через точки (x0, y0), (x1, y1) Интерполяция по
- 63. Пример. N=2 (три узла интерполяции) - уравнение параболы, проходящей через точки (x0, y0), (x1, y1), (x2,
- 65. Обзор методов численного интегрирования Методы вычисления однократных интегралов называются квадратурными (для кратных интегралов – кубатурными). К
- 66. Метод прямоугольников Алгоритм метода прямоугольников: Весь участок [a,b] делим на n равных частей с шагом h=(b-a)/n.
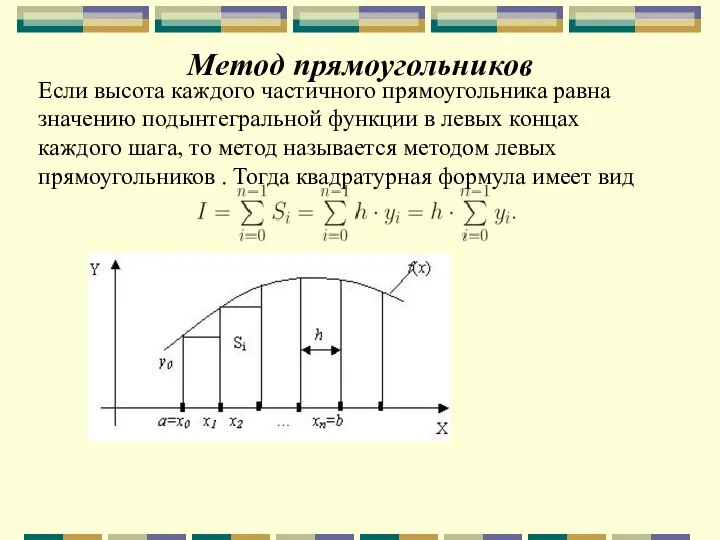
- 67. Метод прямоугольников Если высота каждого частичного прямоугольника равна значению подынтегральной функции в левых концах каждого шага,
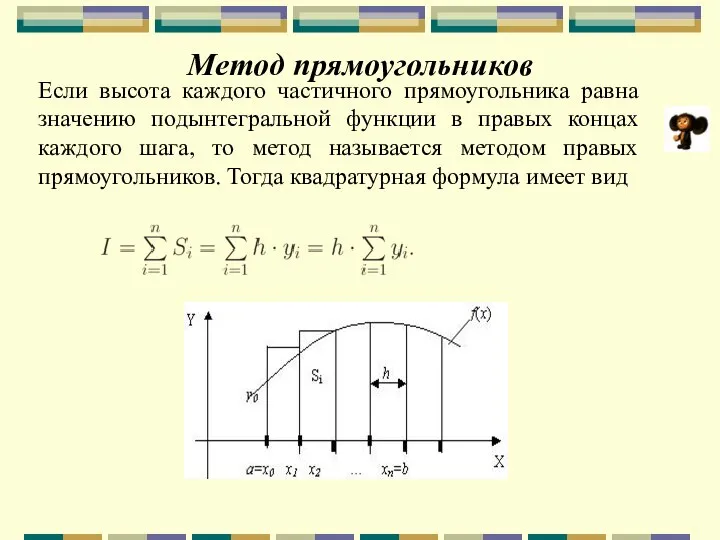
- 68. Метод прямоугольников Если высота каждого частичного прямоугольника равна значению подынтегральной функции в правых концах каждого шага,
- 69. Метод трапеций Найдем площади Si частичных трапеций: Приближенное значение интеграла равно Точность метода трапеций имеет порядок
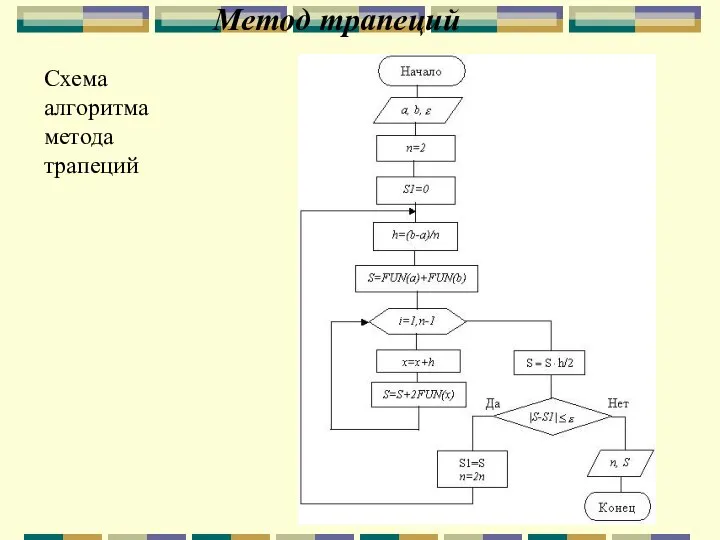
- 70. Метод трапеций Алгоритм метода трапеций: Интервал [a,b] делим на n равных частей с шагом h=(b-a)/n. Вычисляем
- 71. Метод трапеций Найдем площади Si частичных трапеций: Приближенное значение интеграла равно Точность метода трапеций имеет порядок
- 72. Метод трапеций Схема алгоритма метода трапеций
- 73. Метод Симпсона В методе Симпсона в каждой части деления подынтегральная функция аппроксимируется квадратичной параболой a0x2+a1x+a2. В
- 74. Метод Симпсона Исходя из геометрического смысла определенного интеграла, площадь S1 равна определенному интегралу от квадратичной параболы
- 75. Метод Симпсона Решая эту систему, найдем коэффициенты параболы. Для участка [x2, x4] Для участка [xi-1, xi+1]:
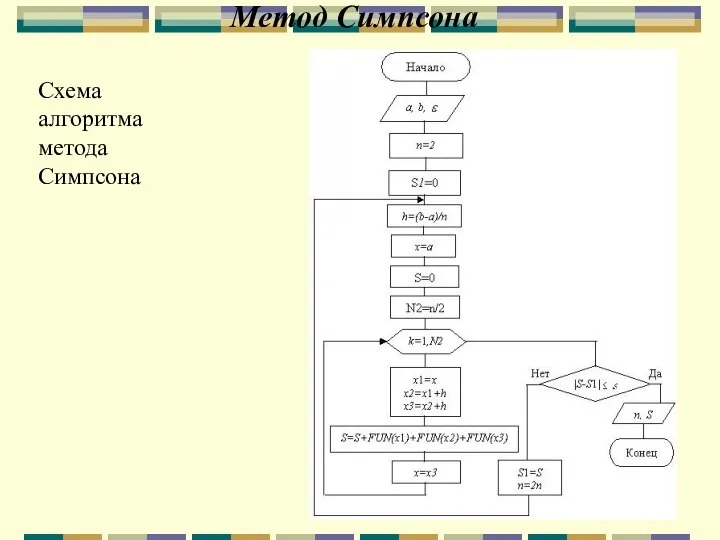
- 76. Метод Симпсона Схема алгоритма метода Симпсона
- 77. Численные методы решения дифференциальных уравнений первого порядка Общий вид дифференциального уравнения Нормальная форма дифференциального уравнения где
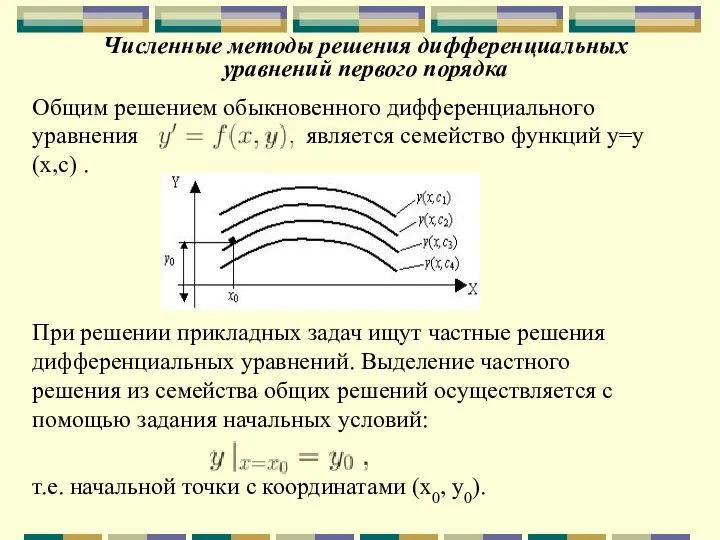
- 78. Численные методы решения дифференциальных уравнений первого порядка Общим решением обыкновенного дифференциального уравнения является семейство функций у=у(х,с)
- 79. Численные методы решения дифференциальных уравнений первого порядка Нахождение частного решения дифференциального уравнения удовлетворяющего начальному условию называется
- 80. Методы Рунге - Кутта Наиболее эффективными и часто встречаемыми методами решениями задачи Коши являются методы Рунге
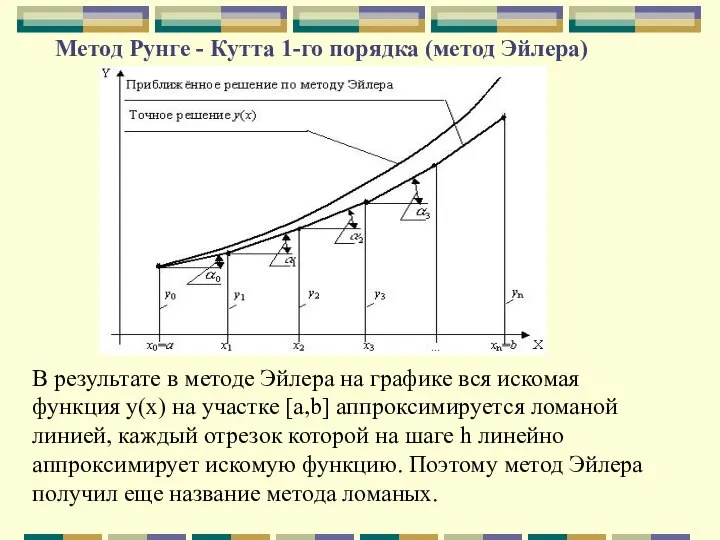
- 81. Метод Рунге - Кутта 1-го порядка (метод Эйлера) Отбросим члены ряда, содержащие h2, h3, h4, тогда
- 82. Метод Рунге - Кутта 1-го порядка (метод Эйлера) В результате в методе Эйлера на графике вся
- 83. Метод Рунге - Кутта 1-го порядка (метод Эйлера) В методе Эйлера наклон касательной в пределах каждого
- 84. Метод Рунге - Кутта 2-го порядка (модифицированный метод Эйлера) Отбросим в разложении в ряд Тейлора члены
- 85. Метод Рунге - Кутта 2-го порядка (модифицированный метод Эйлера) Как видно, для определения функции y(x) в
- 86. Метод Рунге - Кутта 2-го порядка (модифицированный метод Эйлера) На втором этапе уточняем значение yi+1 по
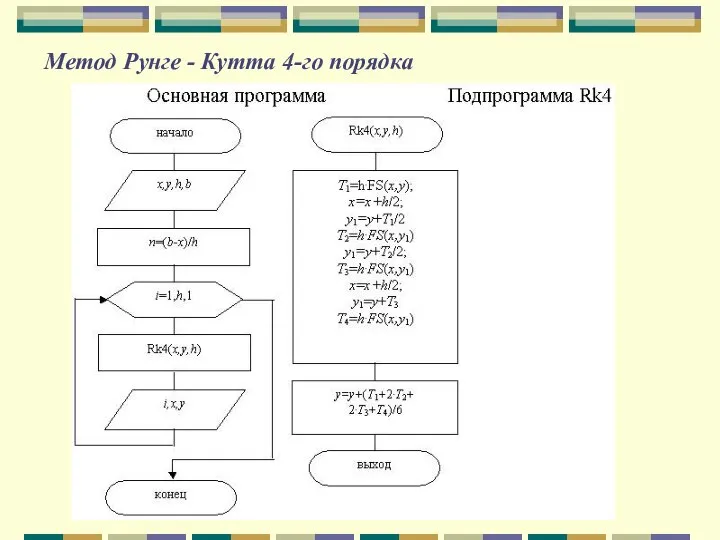
- 87. Метод Рунге - Кутта 4-го порядка Самое большое распространение из всех численных методов решения дифференциальных уравнений
- 88. Метод Рунге - Кутта 4-го порядка Для сохранения членов ряда, содержащих h2,h3,h4 необходимо определить вторую y",
- 89. Метод Рунге - Кутта 4-го порядка
- 90. Решение дифференциальных уравнений высоких порядков Методы Рунге-Кутта можно использовать не только для решения дифференциальных уравнений первого
- 91. Решение дифференциальных уравнений высоких порядков В результате дифференциальное уравнение m -го порядка сводится к системе, состоящей
- 92. Решение дифференциальных уравнений второго порядка Общий вид дифференциальных уравнений второго порядка Нормальная форма дифференциальных уравнений второго
- 93. Решение дифференциальных уравнений второго порядка Сформулируем задачу Коши для системы, состоящей из двух дифференциальных уравнений второго
- 94. Решение дифференциальных уравнений второго порядка На графике решением задачи Коши для системы, состоящей из двух дифференциальных
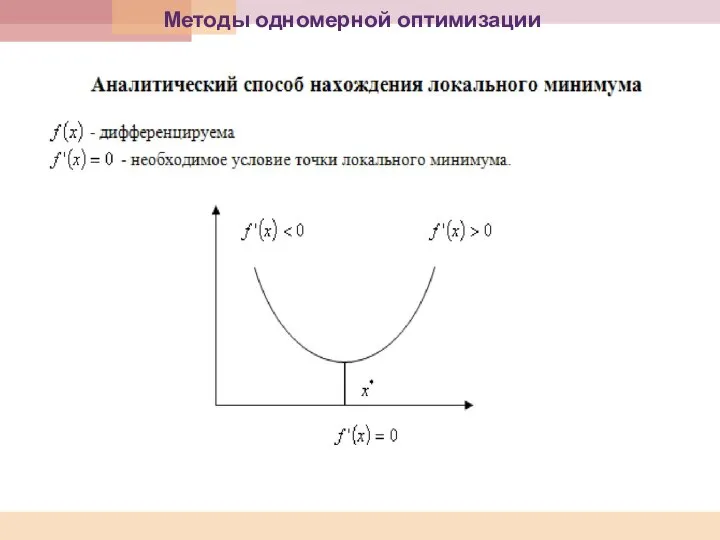
- 95. Методы одномерной оптимизации
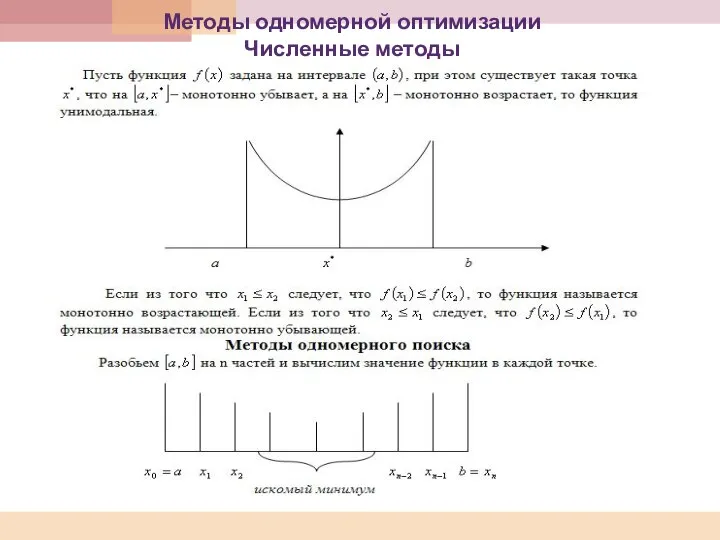
- 96. Методы одномерной оптимизации Численные методы
- 97. Методы одномерной минимизации
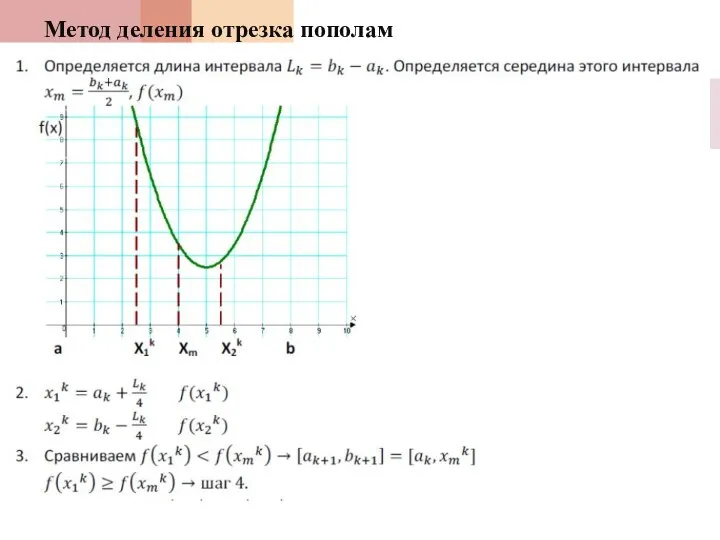
- 98. Метод деления отрезка пополам
- 99. Метод деления отрезка пополам
- 100. Методы одномерной оптимизации
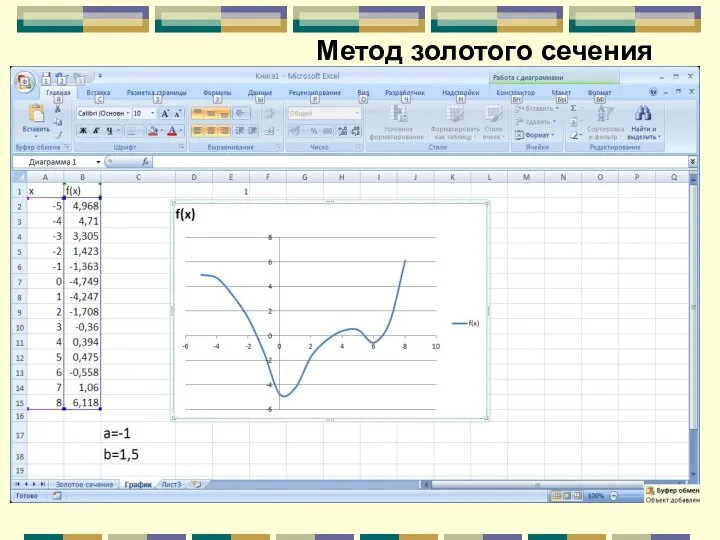
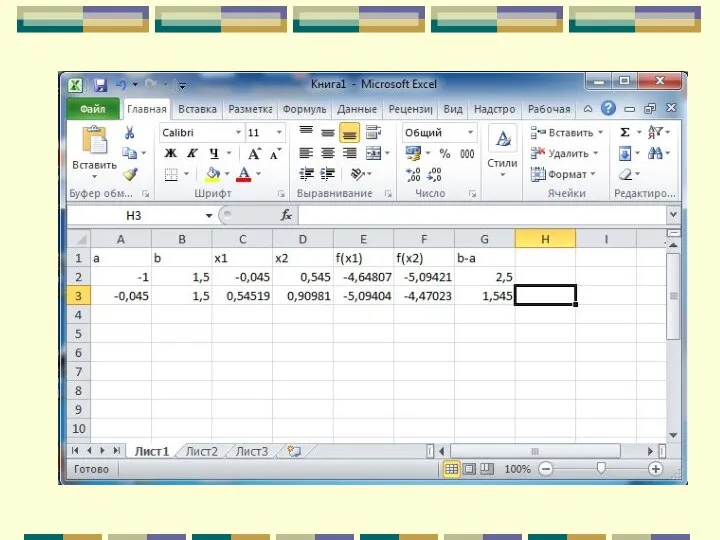
- 101. Методы одномерной оптимизации Пример. Найти минимум функции методом «Золотого сечения»
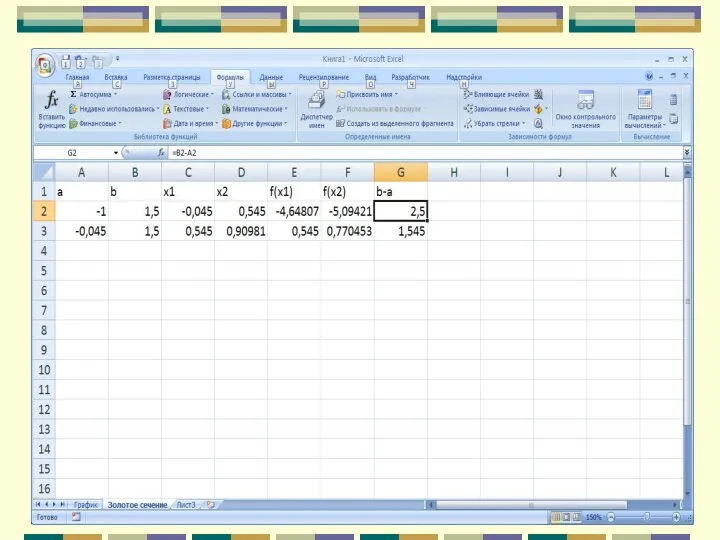
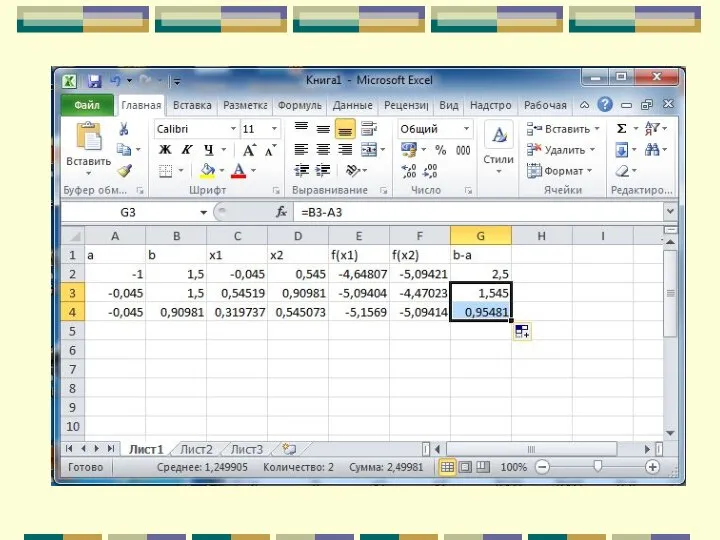
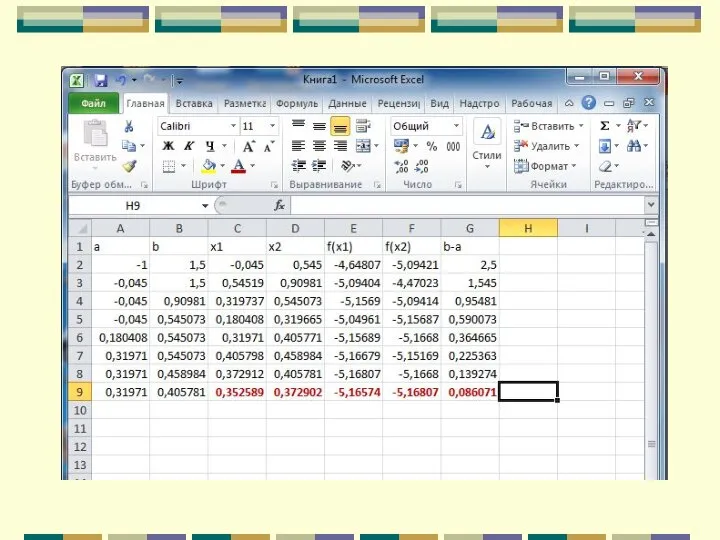
- 102. Метод золотого сечения
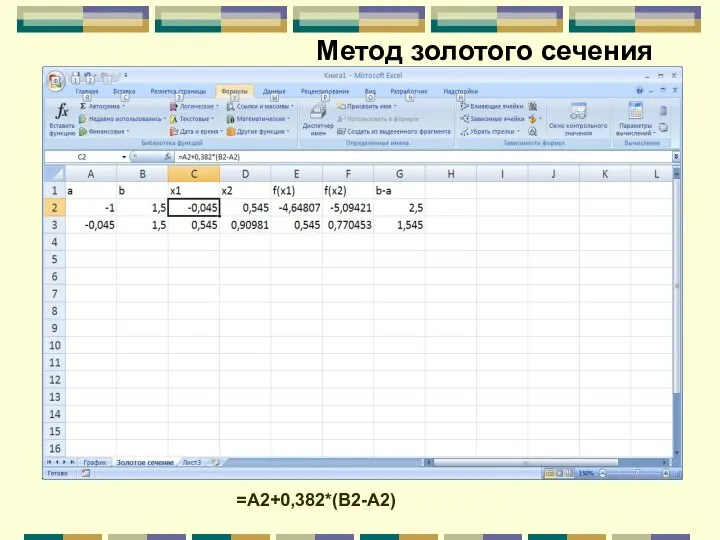
- 103. Метод золотого сечения =A2+0,382*(B2-A2)
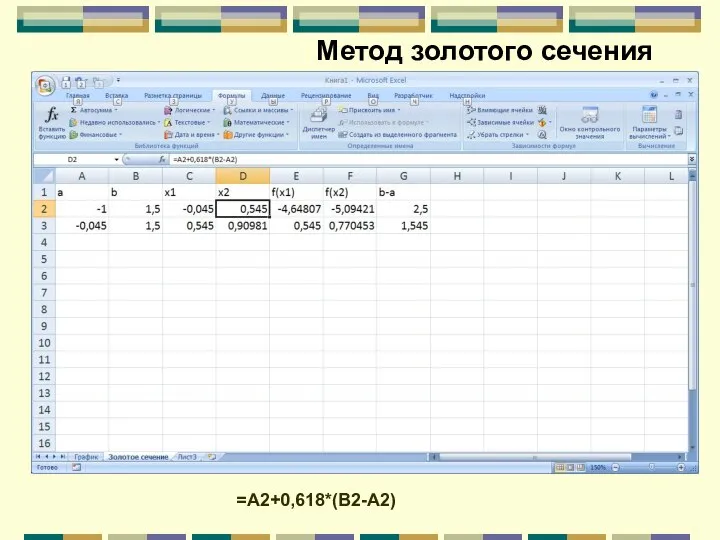
- 104. Метод золотого сечения =A2+0,618*(B2-A2)
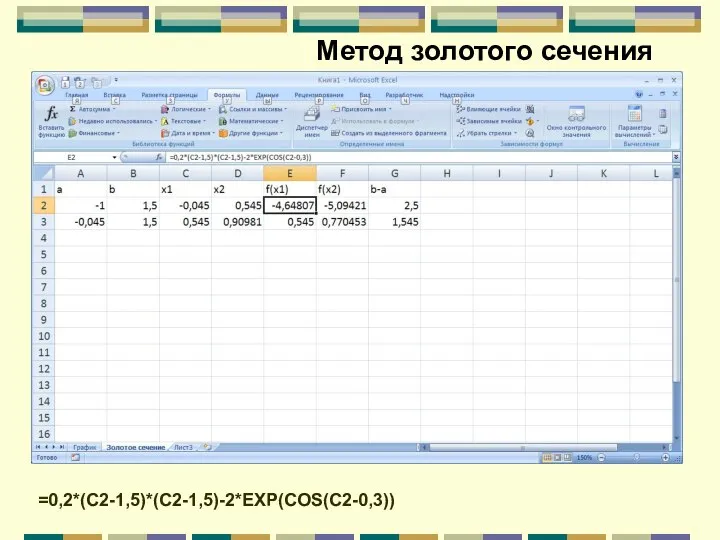
- 105. Метод золотого сечения =0,2*(C2-1,5)*(C2-1,5)-2*EXP(COS(C2-0,3))
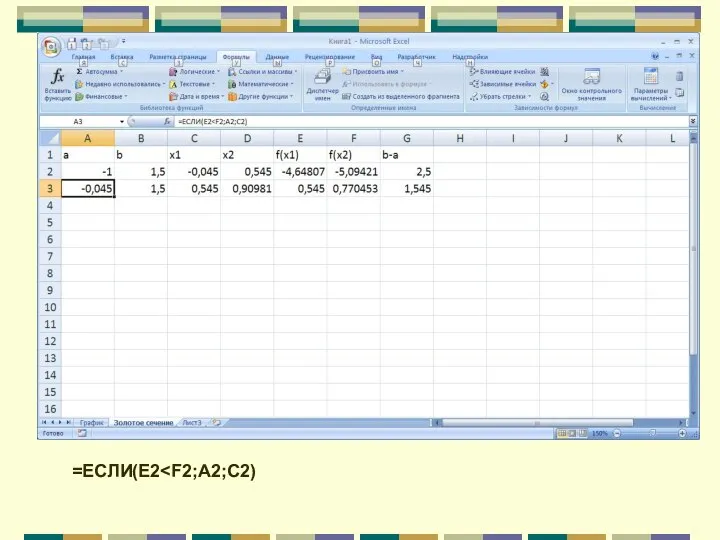
- 107. =ЕСЛИ(E2
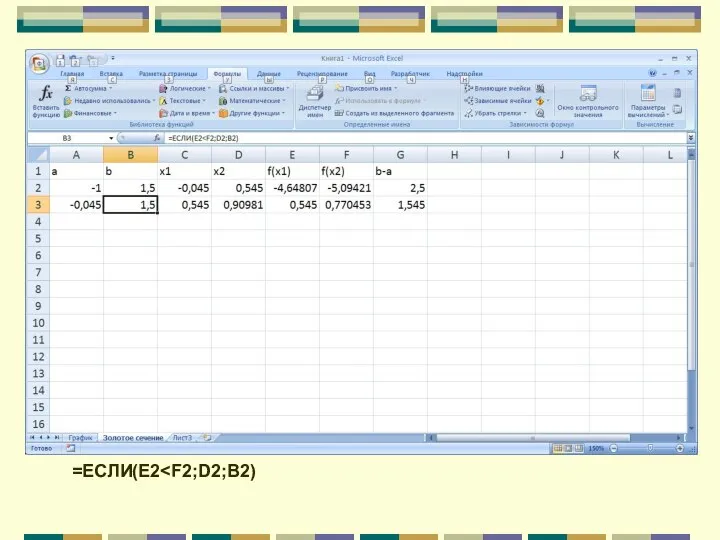
- 108. =ЕСЛИ(E2
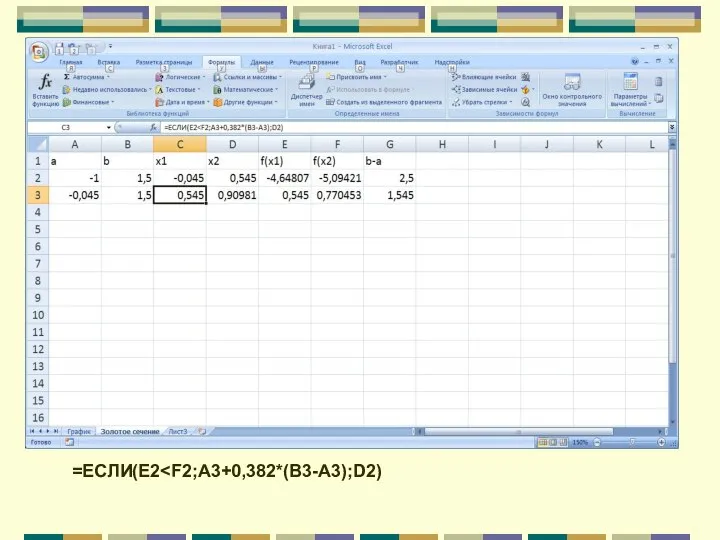
- 109. =ЕСЛИ(E2
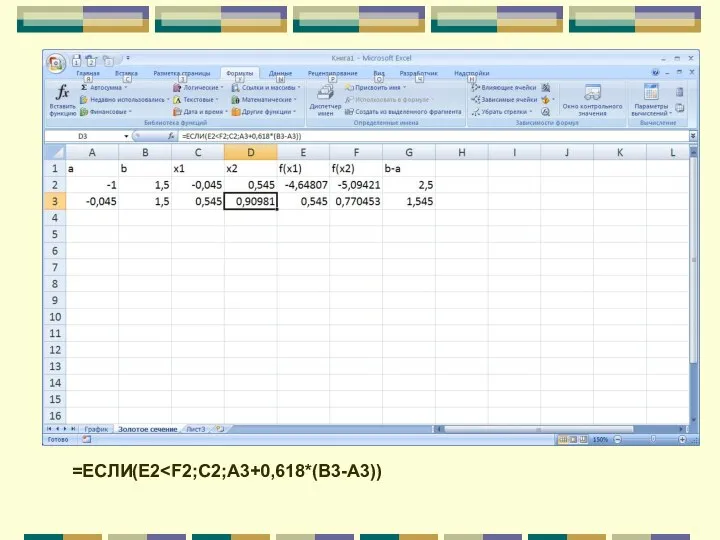
- 110. =ЕСЛИ(E2
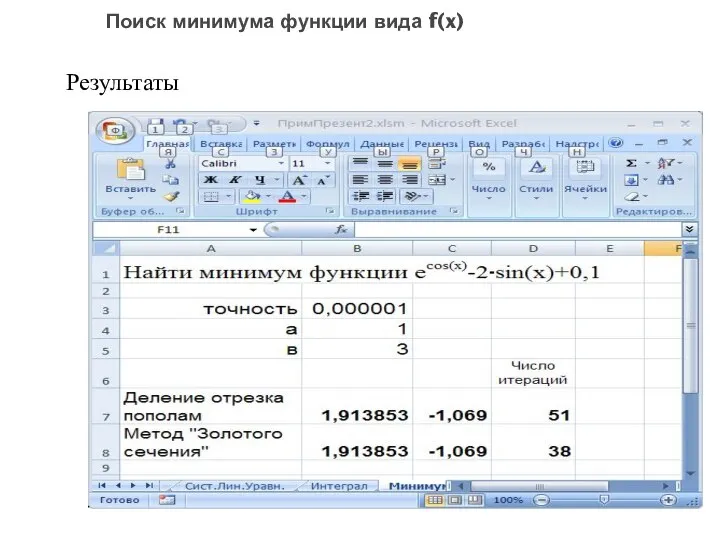
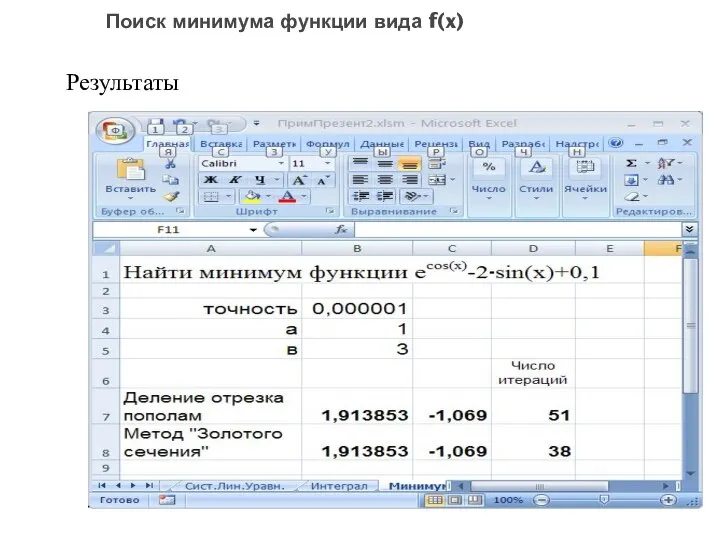
- 114. Результаты Поиск минимума функции вида f(x)
- 115. Результаты Поиск минимума функции вида f(x)
- 116. Логистика - наука о планировании, контроле и управлении транспортированием, складированием и др. материальными и нематериальными операциями,
- 117. Глобальная цель логистики - сокращение цикла, уменьшение запасов. Основная задача логистики - использование материалов, энергии, информации,
- 118. Логистика - нахождение такого канала товародвижения, который обеспечивает минимальные сроки и минимальные затраты по доставке товаров
- 119. Показатели логистики - время поставки; - точность, верность, обязательность поставки; - готовность к поставке; - качество
- 120. Принципы логистики 1. Саморегулирование (сбалансировапнность производства). 2. Гибкость (возможность внесения изменений в график закупки материалов, изменение
- 121. Понятие логистической системы Материальный поток (МП) - совокупность ресурсов одного наименования, находящихся в процессе приложения к
- 122. Информационный поток (ИП) не всегда соответствует дан. МП, т.е. ИП и МП могут быть синхронные и
- 123. В логистике для управления потоками используют функции: - Планирование (установление оптимальной траектории движения, разработка расписания или
- 124. Логистический канал - частично упорядоченное множество, состоящие из поставщика, потребителя, перевозчиков, посредников, страховщиков и т.д. Потребитель
- 125. Логистический цикл в общем виде включает в себя: время на формулировку заказа и его оформление в
- 126. Производственный цикл - часть логистического цикла (от запуска на операцию до полного изготовления). Логистический цикл -
- 127. Материальные ресурсы: - сырье; - основные материалы (материалы, входящие в продукт и составляющие его основу); -
- 128. Материальный поток - материальные ресурсы определенных видов, в определенных количествах перемещаемые от определенного поставщика к определенному
- 129. Разновидности материальных потоков: - по номенклатуре (простые или сложные, одно- или многоассортиментные); - по степени готовности
- 130. Массовые потоки - перемещение которых осуществляется не в единичных транспортных средствах, а в большой их группе,
- 131. По степени совместимости: совместимые несовместимые По способу затаривания грузы: в контейнерах в ящиках в мешках и
- 132. Материальные потоки по степени определенности делятся на: детерминированные стохастические (если отсутствует какая-то характеристика) По ритмичности отправок:
- 133. Материальные потоки делятся на внешние и внутренние. Внешние перемещаются за пределами логистической системы. Внутренние - внутри
- 134. Предметом транспортной логистики является комплекс задач, связанных с организацией перемещения грузов транспортом общего назначения. Задачи транспортной
- 135. Транспорт — это отрасль материального производства, осуществляющая перевозки людей и грузов. В структуре общественного производства транспорт
- 136. Актуальными задачами транспортной логистики являются: координация работы промышленного транспорта с магистральным железнодорожным, водным, автомобильным транспортом, широкое
- 137. По назначению выделяют две основные группы транспорта: Транспорт общего пользования — отрасль современного хозяйства, которая удовлетворяет
- 138. Изменение местонахождения товарно-материальных ценностей с помощью транспортных средств называется транспортировкой грузов. Транспортировка является частью логистического процесса
- 139. Каждая транспортная система состоит из транспортируемых грузов, средств транспорта, процесса транспортировки. Внутрипроизводственная транспортировка подразделяется на межцеховую
- 140. По способу действия все транспортные средства подразделяются на средства прерывного (циклического) и непрерывного действия, по направлению
- 141. Стационарные устройства потребляют малое количество энергии, отличаются небольшими затратами на обслуживание, обладают большей надежностью и безопасностью.
- 142. Задача выбора вида транспорта решается во взаимной связи с другими задачами логистики, такими, как создание и
- 143. Выделяют шесть факторов, влияющих на выбор вида транспорта: время доставки, частота отправлений груза, надежность соблюдения графика
- 144. Экспертная оценка значимости этих факторов показывает, что при выборе транспортного средства в первую очередь принимают во
- 145. Рассмотрим технико-экономические особенности различных видов транспорта, определяющие сферы их рационального использования. Железнодорожный транспорт хорошо приспособлен для
- 146. Межконтинентальные перевозки грузов обеспечивает морской транспорт. Его основными преимуществами являются низкие тарифы, практически неограниченная пропускная и
- 147. Речной транспорт при перевозках грузов весом более 100 т на расстояние свыше 250 км является самым
- 148. Воздушное сообщение в пределах европейских стран редко используется. В основном воздушный транспорт нужен в международных перевозках
- 149. Трубопроводный транспорт обладает тем преимуществом, что прокладка трубопроводов возможна повсеместно. При этом обеспечиваются низкая себестоимость и
- 150. Для ускорения погрузочно-разгрузочных работ, ускорения оборота транспортных средств, улучшения сохранности грузов в этом случае применяются контейнеры
- 151. Характеристики вагонного парка Материально-техническая база транспорта включает транспортные средства (вагоны, локомотивы, флот, автомобили), технические устройства и
- 152. Характеристики вагонного парка Грузоподъёмность - показатель мощности транспортного средства, измеряемый количеством тонн грузов, которые могут быть
- 153. Характеристики вагонного парка Грузовместимость - суммарный объём помещений транспортного средства, используемый для размещения и перевозки грузов.
- 154. Характеристики вагонного парка Коэффициент использования грузоподъёмности вагона определяется отношением средней статистической нагрузки вагона на среднюю его
- 155. Характеристики морских и речных судов Транспортный флот - главный элемент материально-технической базы морского и речного транспорта,
- 156. Характеристики морских и речных судов Грузоподъемность судна - максимальное количество груза (без воды, топлива, грузов снабжения)
- 157. Характеристики морских и речных судов Коэффициент использования грузовместимости определяется по следующим формулам: для простого рейса (при
- 158. Характеристики автомобильного транспорта Подвижной состав автомобильного транспорта состоит из автомобилей, тягачей, прицепов и полуприцепов. Грузоподъемность автотранспорта
- 159. Характеристики автомобильного транспорта Коэффициент использования грузоподъемности автомобиля характеризует использование номинальной грузоподъемности автомобиля в статике и динамике.
- 160. Характеристики автомобильного транспорта Динамический коэффициент есть отношение фактических тонно-километров к возможным тонно-километрам при полном использовании грузоподъемности.
- 161. Характеристики автомобильного транспорта Оборот включает одну или несколько ездок, причем подвижной состав обязательно должен возвращаться в
- 162. Характеристики автомобильного транспорта К первой группе относятся показатели, характеризующие степень использования подвижного состава: коэффициенты технической готовности,
- 163. Характеристики автомобильного транспорта Вторая группа характеризует результативность работы подвижного состава: количество ездок, общее расстояние перевозки и
- 164. Характеристики автомобильного транспорта
- 165. Характеристики автомобильного транспорта
- 166. Характеристики автомобильного транспорта
- 167. Характеристики автомобильного транспорта
- 168. В логистике транспорта важно знатъ, насколько эффективно организован процесс транспортировки грузов. Необходимой информацией для подобных расчетов
- 169. Транспортный тариф рассчитывается на среднюю дальность перевозки в определенных пределах; средняя дальность перевозки называется тарифным поясом.
- 170. Железнодорожные транспортные тарифы рассчитываются на основе прейскуранта «Тарифы на грузовые железнодорожные перевозки» № 10-01, который был
- 171. Тарифы автомобильного транспорта включают в себя надбавки за перевозку грузов в специализированных автомобилях, что связано с
- 172. Управление процессом транспортировки грузов на практике осуществляется путем использования организованного документирования и документооборота, а также информатизации
- 173. Для железнодорожного транспорта первичным документом, который имеет силу договора, выступает накладная, составляемая отправителем. Кроме того, в
- 174. Для решения задач оптимизации необходимо обеспечить контроль за всеми звеньями системы перемещения грузов. Оптимизация по критерию
- 175. Возникает ряд проблем - предприятие должно решить, в какой мере затраты, связанные с сокращением времени товародвижения
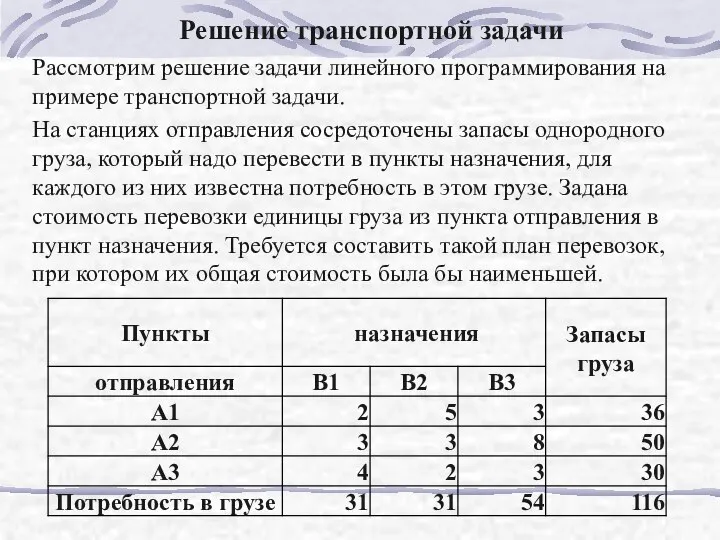
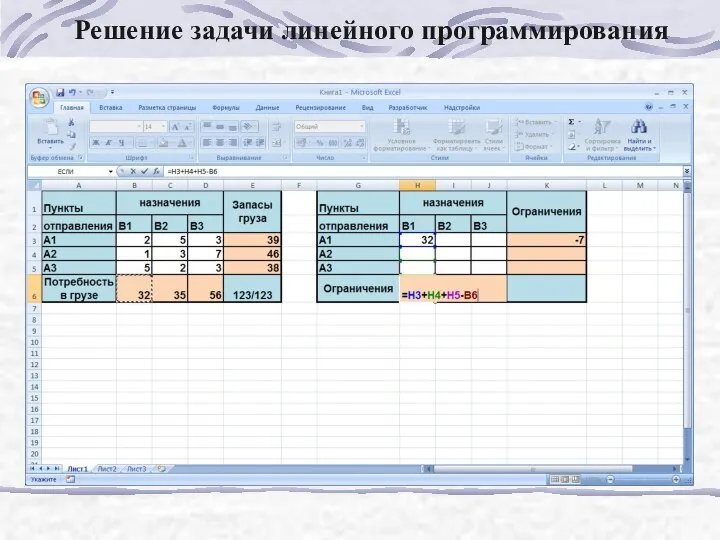
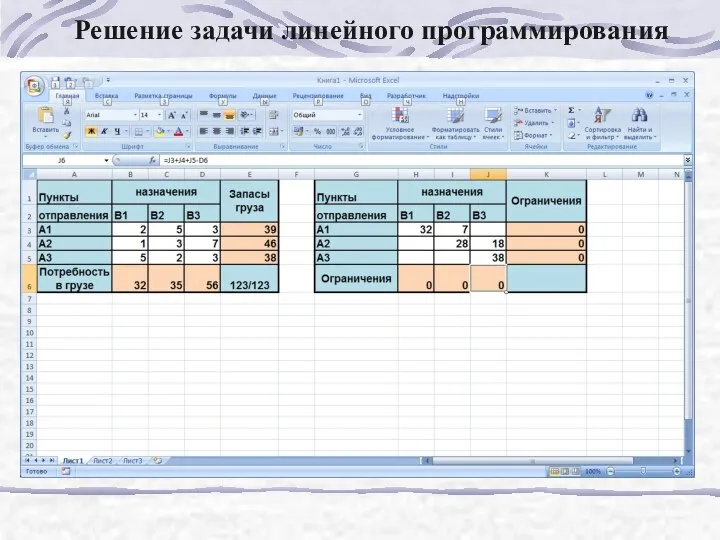
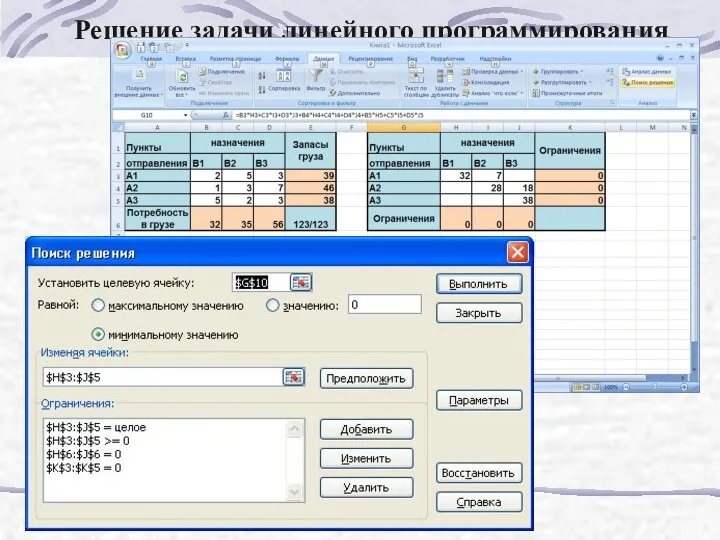
- 176. Решение транспортной задачи Рассмотрим решение задачи линейного программирования на примере транспортной задачи. На станциях отправления сосредоточены
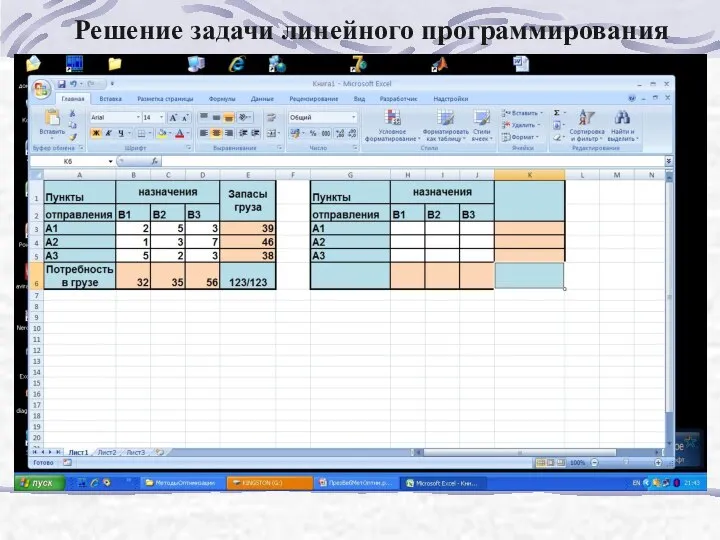
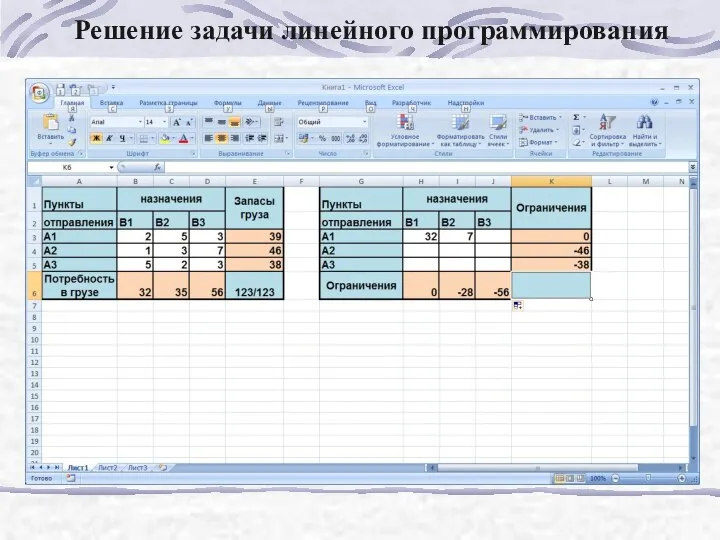
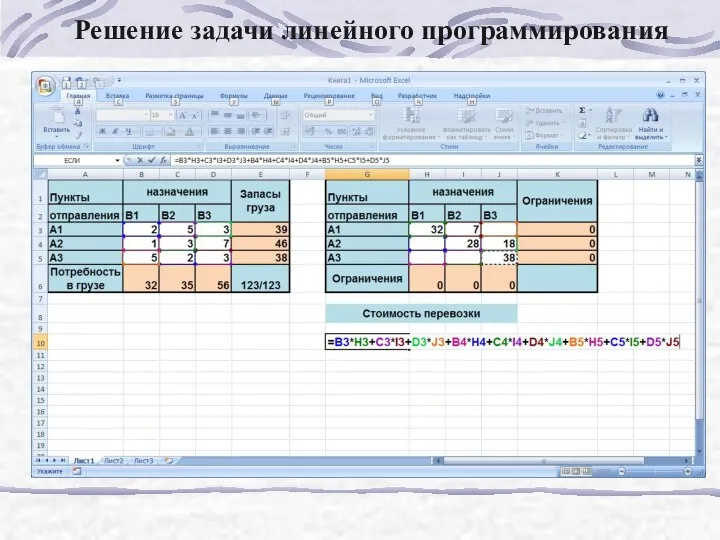
- 177. Решение задачи линейного программирования
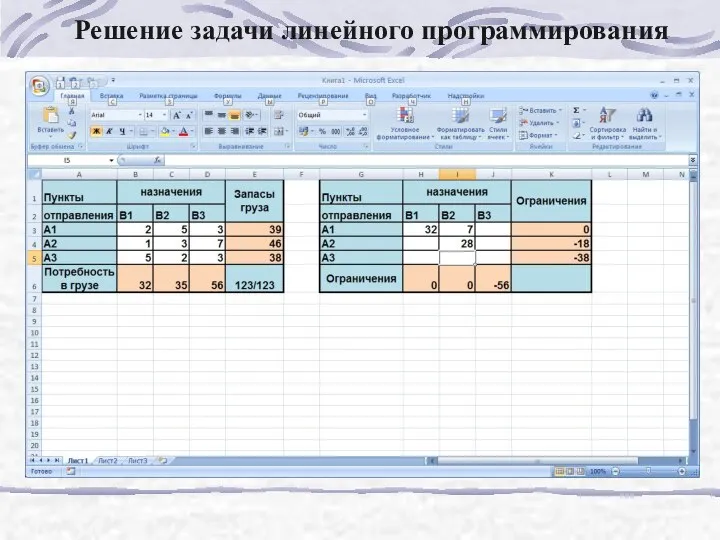
- 178. Решение задачи линейного программирования
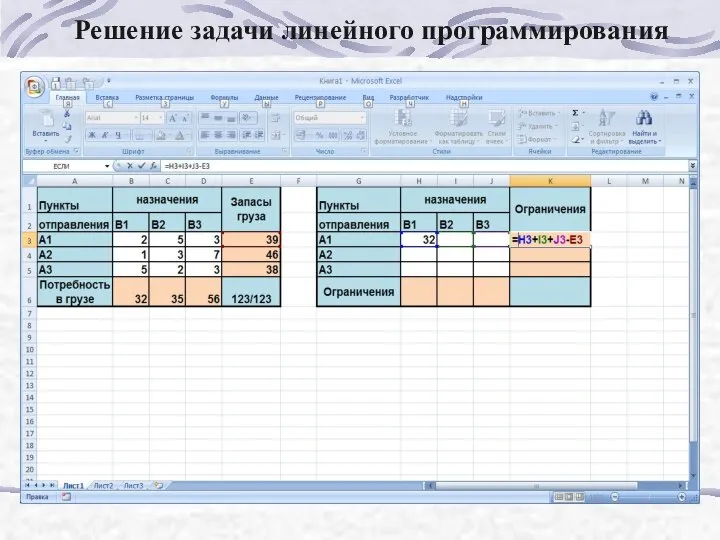
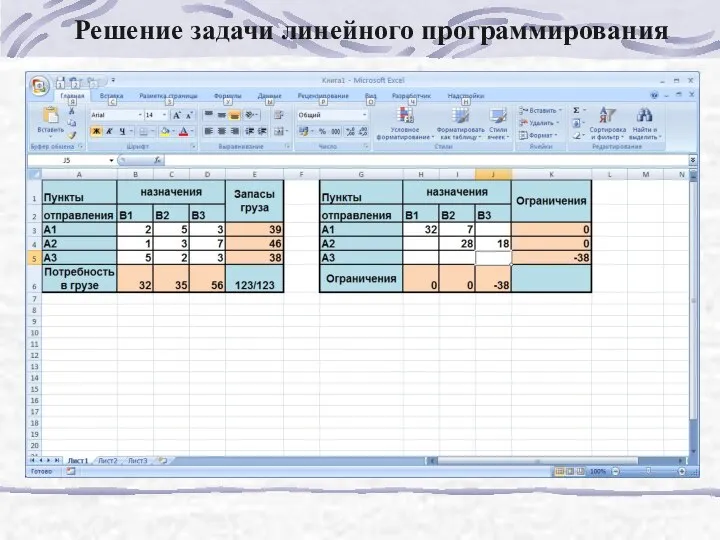
- 179. Решение задачи линейного программирования
- 180. Решение задачи линейного программирования
- 181. Решение задачи линейного программирования
- 182. Решение задачи линейного программирования
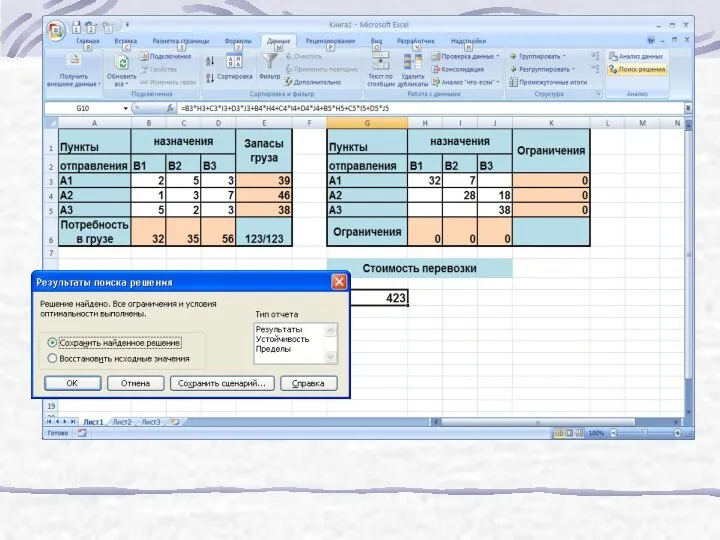
- 183. Решение задачи линейного программирования
- 184. Решение задачи линейного программирования
- 185. Решение задачи линейного программирования
- 186. Решение задачи линейного программирования
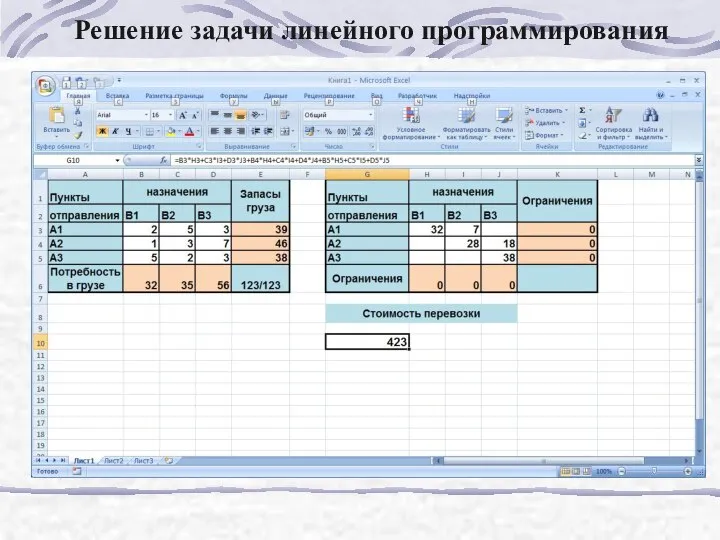
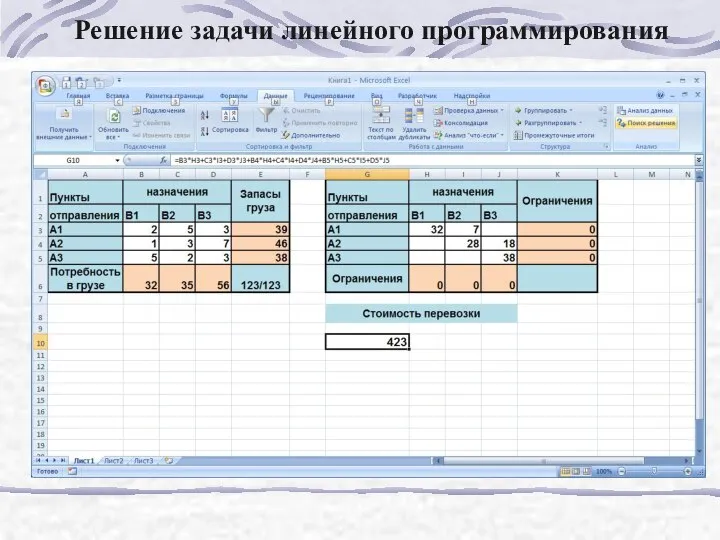
- 187. Решение задачи линейного программирования
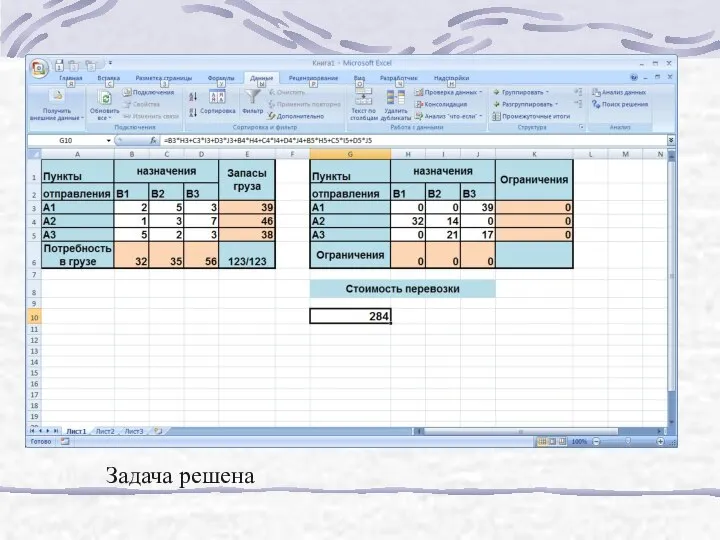
- 189. Задача решена
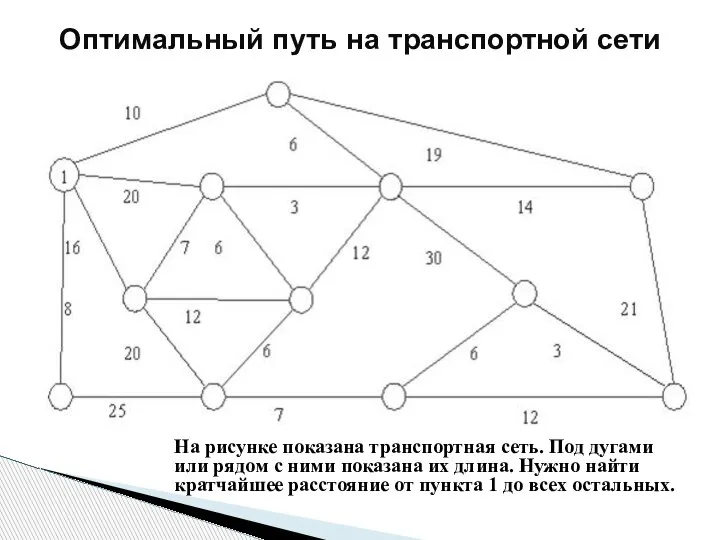
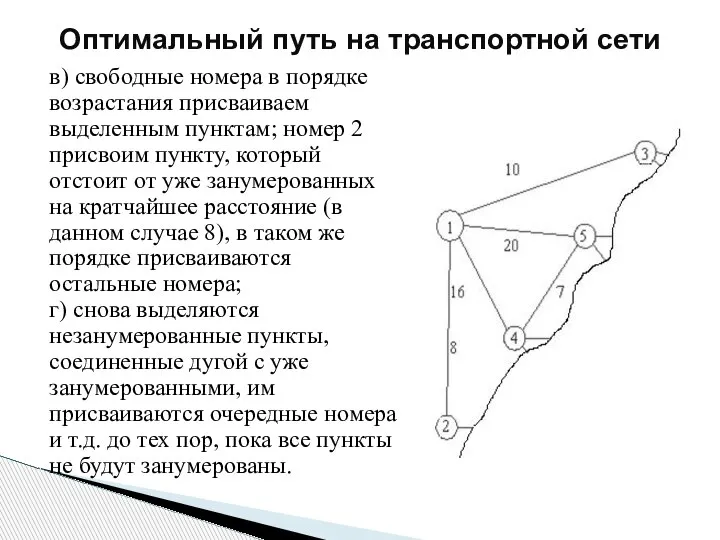
- 190. На рисунке показана транспортная сеть. Под дугами или рядом с ними показана их длина. Нужно найти
- 191. Применим метод потенциалов. Потенциал – это длина кратчайшего путь от начального (первого) пункта до данного. Чтобы
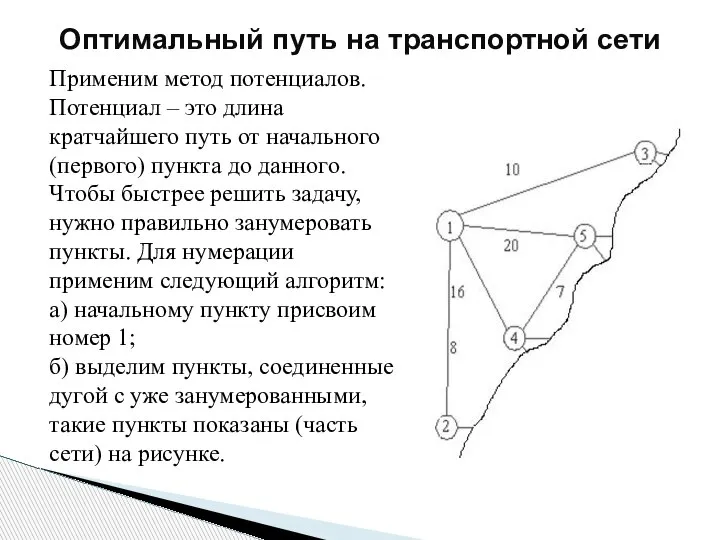
- 192. в) свободные номера в порядке возрастания присваиваем выделенным пунктам; номер 2 присвоим пункту, который отстоит от
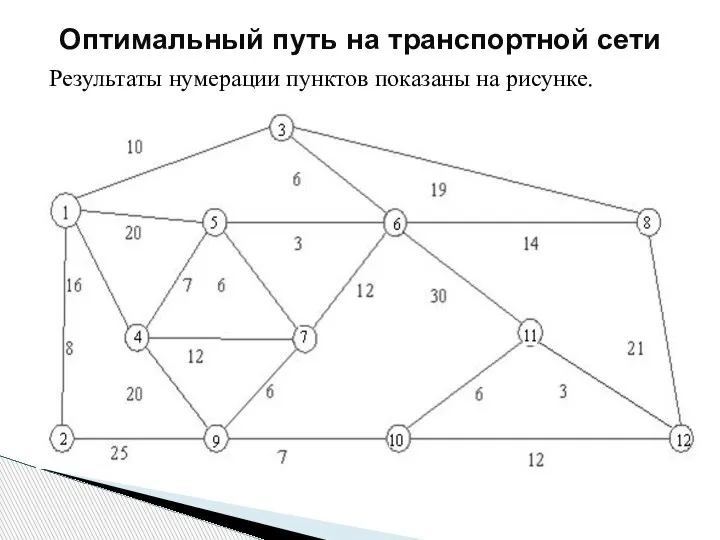
- 193. Результаты нумерации пунктов показаны на рисунке. Оптимальный путь на транспортной сети
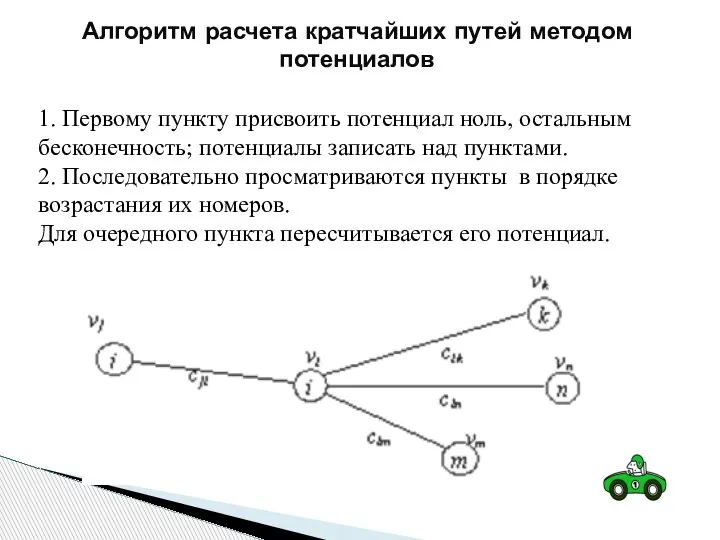
- 194. 1. Первому пункту присвоить потенциал ноль, остальным бесконечность; потенциалы записать над пунктами. 2. Последовательно просматриваются пункты
- 195. На рисунке показан пункт i, для которого пересчитывается его потенциал, а пункты j, k, m, n
- 196. 3. После пересчета потенциалов для всех пунктов, нужно начать процедуру пересчета заново. И делать это до
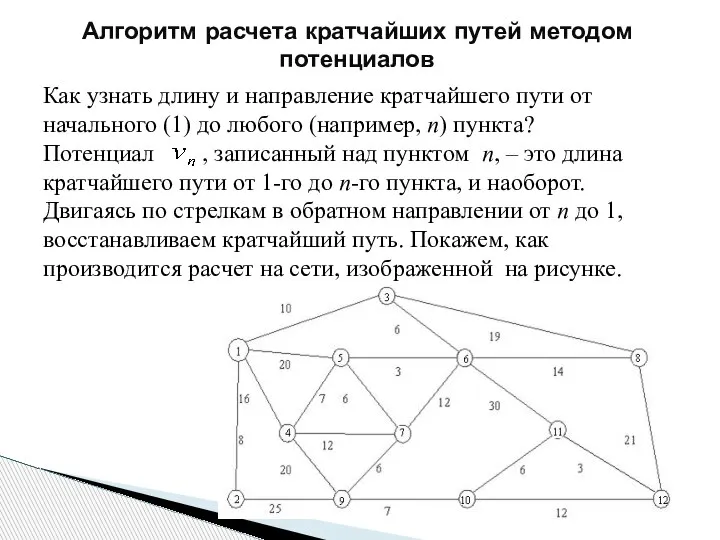
- 197. Алгоритм расчета кратчайших путей методом потенциалов Как узнать длину и направление кратчайшего пути от начального (1)
- 198. Алгоритм расчета кратчайших путей методом потенциалов
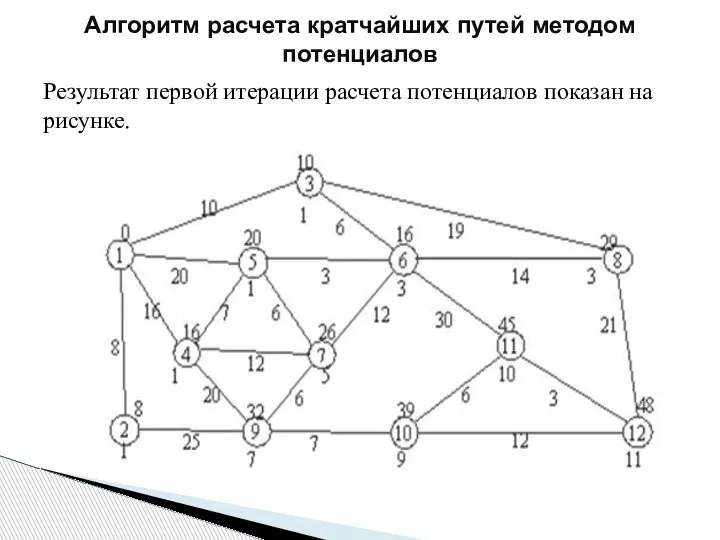
- 199. Результат первой итерации расчета потенциалов показан на рисунке. Алгоритм расчета кратчайших путей методом потенциалов
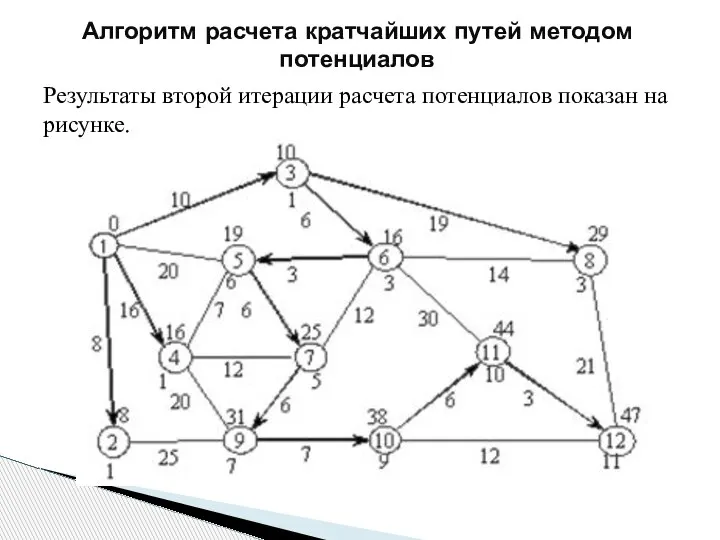
- 200. Алгоритм расчета кратчайших путей методом потенциалов Начинаем вторую итерацию. Снова проходим по всем пунктам в порядке
- 201. Алгоритм расчета кратчайших путей методом потенциалов Результаты второй итерации расчета потенциалов показан на рисунке.
- 202. Алгоритм расчета кратчайших путей методом потенциалов Переходим к третьей итерации. Пересчитываем потенциалы, пытаясь их уменьшить. Но
- 203. Алгоритм расчета кратчайших путей методом потенциалов Например, нужно определить оптимальный путь между пунктами 1 и 8.
- 204. Задача коммивояжера Задача коммивояжера (ЗК) является одной из знаменитых задач теории комбинаторики. Она была поставлена в
- 205. Задача коммивояжера Чтобы привести задачу к математическому виду, введём некоторые термины. Итак, города перенумерованы числами j=(1,2,3..n).
- 206. Задача коммивояжера Относительно математизированной формулировки ЗК уместно сделать два замечания. Во-первых, в постановке Сij означали расстояния,
- 207. Задача коммивояжера В математической постановке говорится о произвольной матрице. Сделано это потому, что имеется много прикладных
- 208. Задача коммивояжера Второе замечание касается числа всех возможных туров. В несимметричной ЗК все туры t=(j1,j2,..,jn,j1) и
- 209. Задача коммивояжера Незамкнутый гамильтонов цикл называется гамильтоновой цепью (гамильтоновым путём). В терминах теории графов симметричную ЗК
- 210. Задача коммивояжера. Метод ветвей и границ К идее метода ветвей и границ приходили многие исследователи, но
- 211. Задача коммивояжера. Метод ветвей и границ Общая идея тривиальна: нужно разделить огромное число перебираемых вариантов на
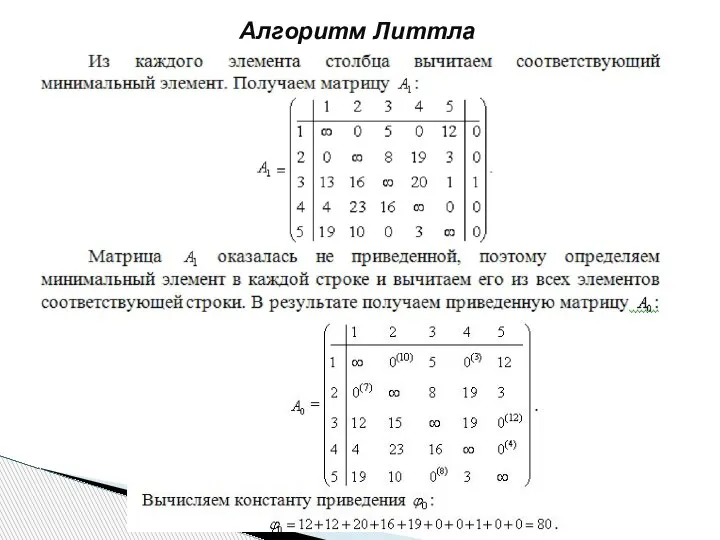
- 212. Алгоритм Литтла Коммивояжер должен посетить пять городов, заезжая в каждый город по одному разу. Расстояние между
- 213. Алгоритм Литтла Сначала получим приведенный вид данной матрицы. Для этого пронумеруем строки и столбцы. В каждом
- 214. Алгоритм Литтла .
- 215. Алгоритм Литтла .
- 216. Алгоритм Литтла .
- 217. Алгоритм Литтла .
- 218. Алгоритм Литтла .
- 219. Алгоритм Литтла .
- 220. Алгоритм Литтла .
- 221. Алгоритм Литтла .
- 222. Алгоритм Литтла .
- 223. Алгоритм Литтла .
- 224. Алгоритм Литтла .
- 225. Алгоритм Литтла .
- 226. Алгоритм Литтла .
- 227. Алгоритм Литтла .
- 229. Скачать презентацию





























![Численные методы решения нелинейных уравнений Процесс определения интервала изоляции [a,b], содержащего только](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1167244/slide-33.jpg)

























![Метод прямоугольников Алгоритм метода прямоугольников: Весь участок [a,b] делим на n равных](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1167244/slide-65.jpg)

![Метод трапеций Алгоритм метода трапеций: Интервал [a,b] делим на n равных частей](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1167244/slide-69.jpg)



![Метод Симпсона Решая эту систему, найдем коэффициенты параболы. Для участка [x2, x4]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1167244/slide-74.jpg)












































































































 Электрический ток в газах и в вакууме
Электрический ток в газах и в вакууме Биологическое действие радиации
Биологическое действие радиации Байесовские процедуры принятия решений о состоянии объектов авиационного оборудования
Байесовские процедуры принятия решений о состоянии объектов авиационного оборудования Свойства воздуха
Свойства воздуха Кривошипно-шатунный механизм двигателя (КШМ)
Кривошипно-шатунный механизм двигателя (КШМ) Устройство для наматывания нижней нити на шпульку
Устройство для наматывания нижней нити на шпульку Hydraulik Steuerblock B35/40/50D Mk4/5
Hydraulik Steuerblock B35/40/50D Mk4/5 Работа силы тяжести
Работа силы тяжести Механика деформируемого твердого тела
Механика деформируемого твердого тела Работа и мощность
Работа и мощность Сила Архимеда. Причина возникновения. Способы измерения
Сила Архимеда. Причина возникновения. Способы измерения Презентация на тему Применение фотоэффекта в солнечных батареях
Презентация на тему Применение фотоэффекта в солнечных батареях  Ультразвук: определение, механизм действия, применение в косметологии
Ультразвук: определение, механизм действия, применение в косметологии Последовательное соединение
Последовательное соединение Марковские процессы
Марковские процессы Автоматизированная информационная система Техосмотр
Автоматизированная информационная система Техосмотр Презентация на тему Движение тела, брошенного вертикально вверх
Презентация на тему Движение тела, брошенного вертикально вверх  Закон сохранения энергии
Закон сохранения энергии Сила Лоренца
Сила Лоренца Параметрический метод диагностирования гидропривода
Параметрический метод диагностирования гидропривода Датчики термоанемометров
Датчики термоанемометров L- jetronic
L- jetronic Электромагнитная природа света. Электромагнитные явления
Электромагнитная природа света. Электромагнитные явления Плавание судов
Плавание судов Электрический ток в различных средах
Электрический ток в различных средах Электрический ток
Электрический ток Уравнение газа состояния идеального
Уравнение газа состояния идеального Общие сведения о системах радиосвязи. Электропитание средств связи
Общие сведения о системах радиосвязи. Электропитание средств связи