Содержание
- 2. R O Определение сферы и её элементов. Сферой называется поверхность, состоящая из точек пространства, расположенных на
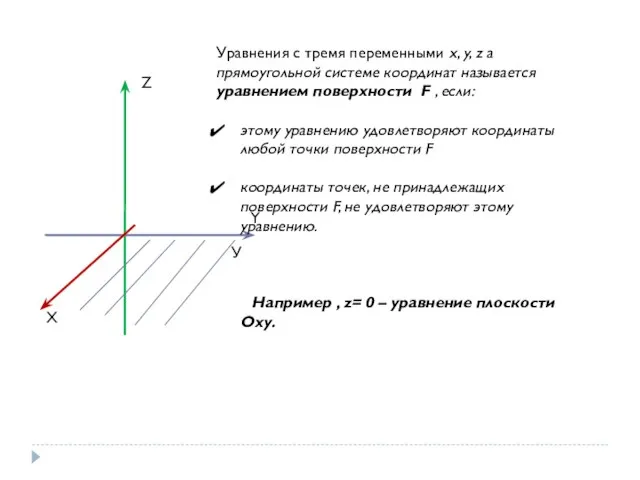
- 3. Z Y X Уравнения с тремя переменными x, y, z а прямоугольной системе координат называется уравнением
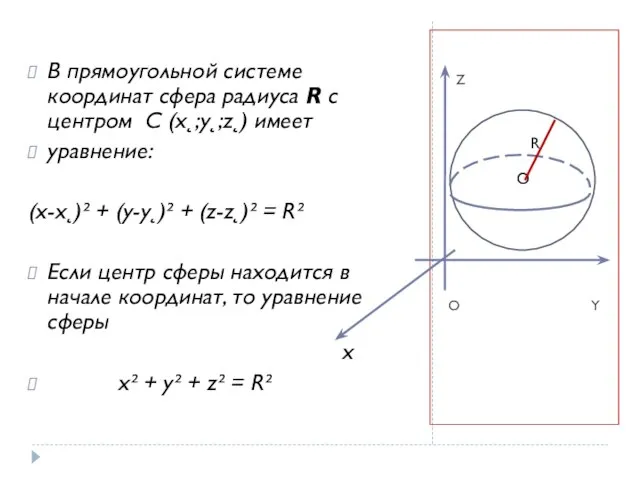
- 4. Z O Y В прямоугольной системе координат сфера радиуса R с центром C (x˛;y˛;z˛) имеет уравнение:
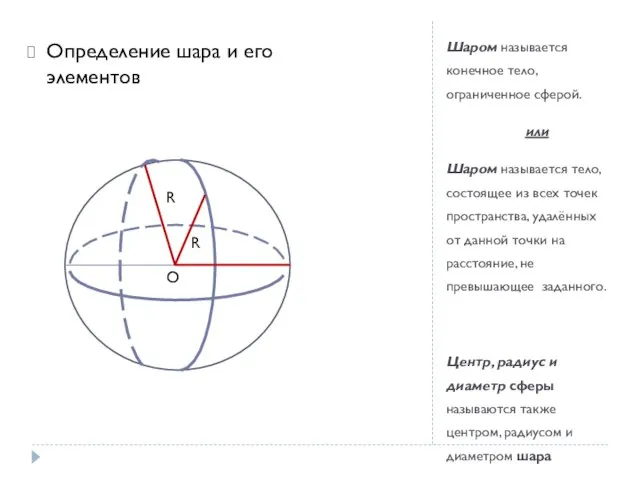
- 5. Шаром называется конечное тело, ограниченное сферой. или Шаром называется тело, состоящее из всех точек пространства, удалённых
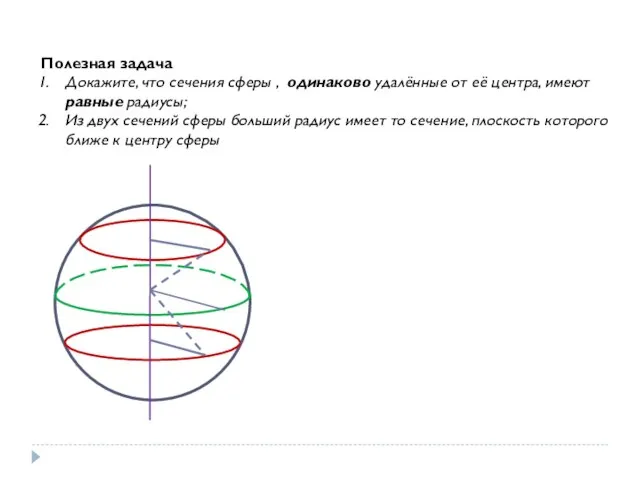
- 6. Полезная задача Докажите, что сечения сферы , одинаково удалённые от её центра, имеют равные радиусы; Из
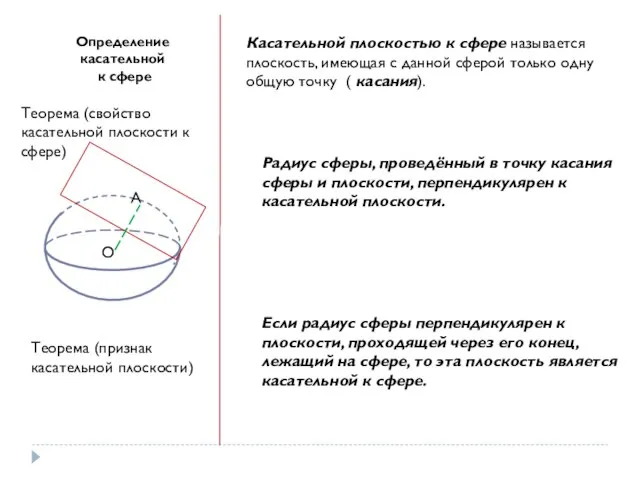
- 7. Определение касательной к сфере Касательной плоскостью к сфере называется плоскость, имеющая с данной сферой только одну
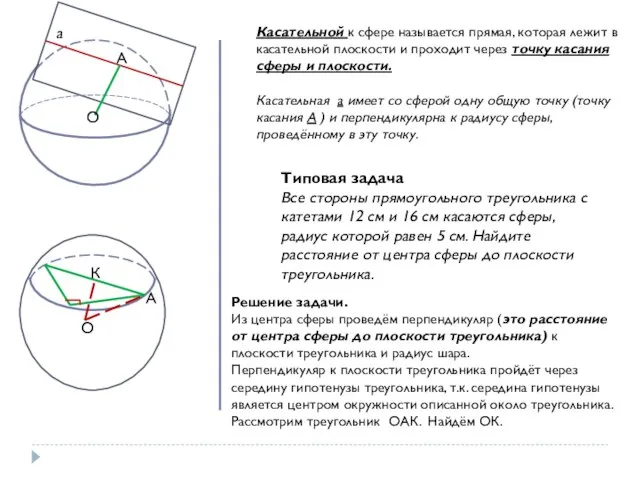
- 8. О А Касательной к сфере называется прямая, которая лежит в касательной плоскости и проходит через точку
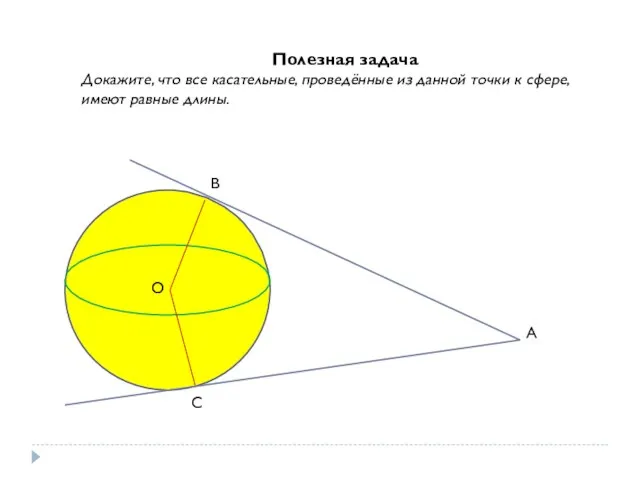
- 9. Полезная задача Докажите, что все касательные, проведённые из данной точки к сфере, имеют равные длины. О
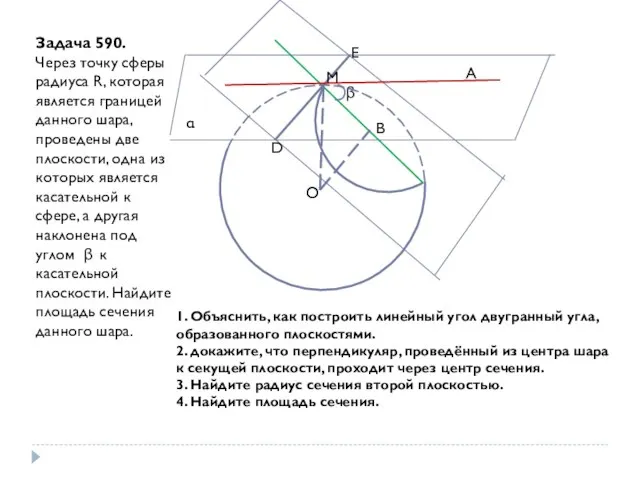
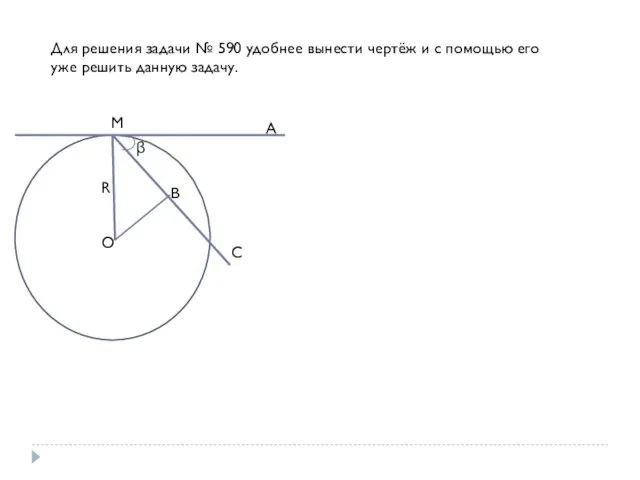
- 10. Задача 590. Через точку сферы радиуса R, которая является границей данного шара, проведены две плоскости, одна
- 11. Для решения задачи № 590 удобнее вынести чертёж и с помощью его уже решить данную задачу.
- 13. Скачать презентацию

 Построение четвёртого пропорционального отрезка
Построение четвёртого пропорционального отрезка Четыре замечательные точки треугольника
Четыре замечательные точки треугольника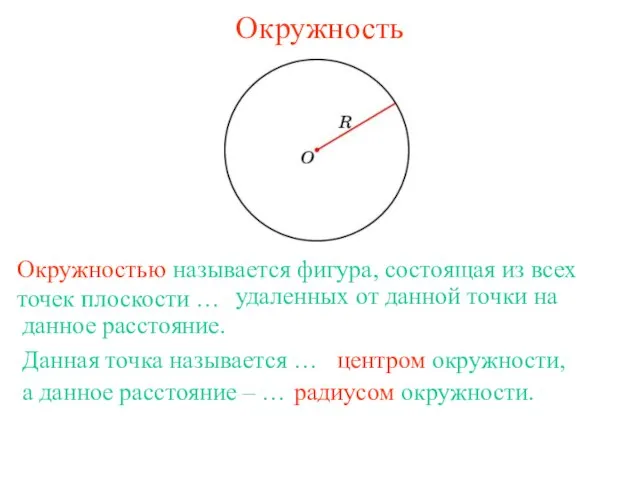 Окружность
Окружность Первый признак равенства треугольников
Первый признак равенства треугольников Геометрия
Геометрия Подготовлю справочник по геометрии (или как повторить геометрию к экзамену)
Подготовлю справочник по геометрии (или как повторить геометрию к экзамену) Гипотеза пуанкаре и терстона
Гипотеза пуанкаре и терстона Площади
Площади Циклоида
Циклоида Планиметрия - презентация по Геометрии_
Планиметрия - презентация по Геометрии_ Площадь параллелограмма 9 класс
Площадь параллелограмма 9 класс Соотношения между сторонами и углами прямоугольного треугольника
Соотношения между сторонами и углами прямоугольного треугольника Геометрия. Как она возникла?
Геометрия. Как она возникла? Основные труды и биография Декарта
Основные труды и биография Декарта Признаки равенства треугольников
Признаки равенства треугольников Двумерный симплекс история его изучения
Двумерный симплекс история его изучения Применение подобия к доказательству теорем и решению задач
Применение подобия к доказательству теорем и решению задач Правильные многогранники
Правильные многогранники Презентация на тему: Сечение
Презентация на тему: Сечение Параллелограмм
Параллелограмм Площади многоугольников
Площади многоугольников Разрезание и складывание плоских фигур
Разрезание и складывание плоских фигур В гостях у Геометрии - презентация по Геометрии_
В гостях у Геометрии - презентация по Геометрии_ Многогранники вокруг нас
Многогранники вокруг нас Площади (8 класс)
Площади (8 класс) Скрещивающиеся прямые. Углы с сонаправленными сторонами. Угол между прямыми
Скрещивающиеся прямые. Углы с сонаправленными сторонами. Угол между прямыми Классическое определение вероятности. Комбинаторные методы решения задач
Классическое определение вероятности. Комбинаторные методы решения задач Медиана, биссектриса и высота треугольника
Медиана, биссектриса и высота треугольника