Содержание
- 2. Цели урока: 1.Знать определение синуса, косинуса, тангенса и котангенса. 2.Уметь применять эти определения к решению примеров
- 3. План урока История развития тригонометрии. Повторение курса геометрии. Изучение нового материала. Закрепление
- 4. Историческая справка тригонон Тригонометрия метрио (измерение треугольника)
- 5. Древний Вавилон-умели предсказывать солнечные и лунные затмения. Древнегреческие учёные-составили таблицы хорд(первые тригонометрические таблицы) Учёные Индии и
- 6. Большой вклад в развитие тригонометрии внесли: Гиппарх Птолемей Франсуа Виет Эйлер Бернулли
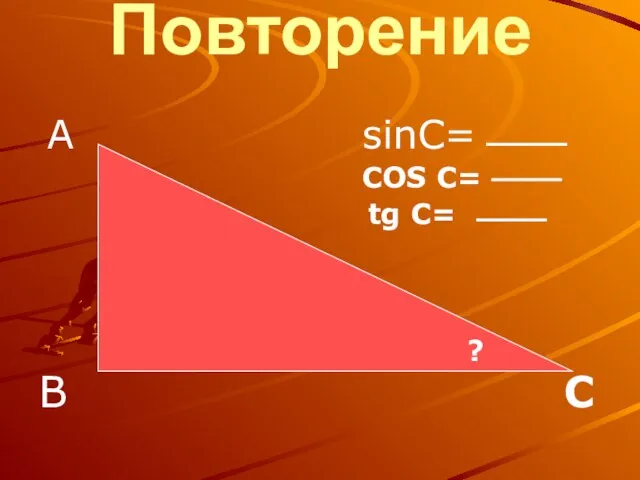
- 7. Повторение А sinC= COS C= tg C= В С ?
- 8. Повторение Для единичной полуокружности y у SIN A = = Y R X COS A= =
- 9. Повторение Основное тригонометрическое тождество: SIN2 X+COS2 Х=1
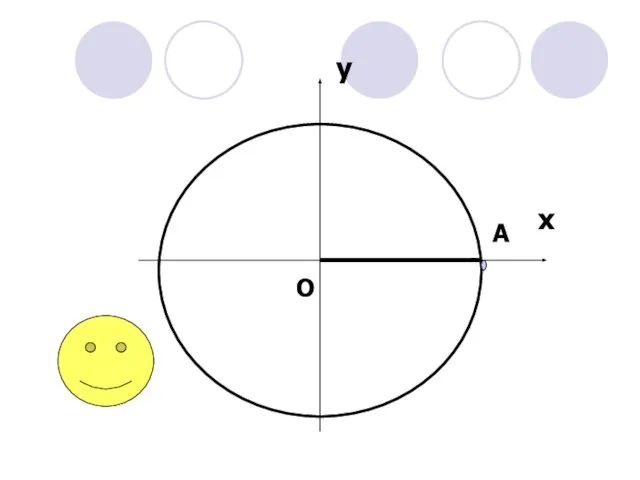
- 10. у х А О
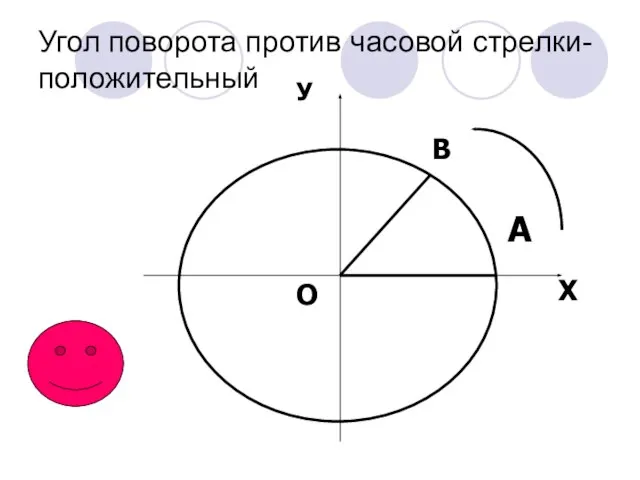
- 11. Угол поворота против часовой стрелки- положительный А О В У Х
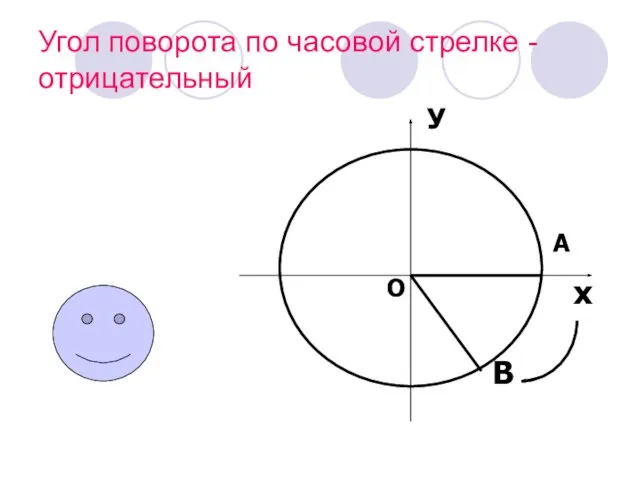
- 12. Угол поворота по часовой стрелке - отрицательный О х У А В
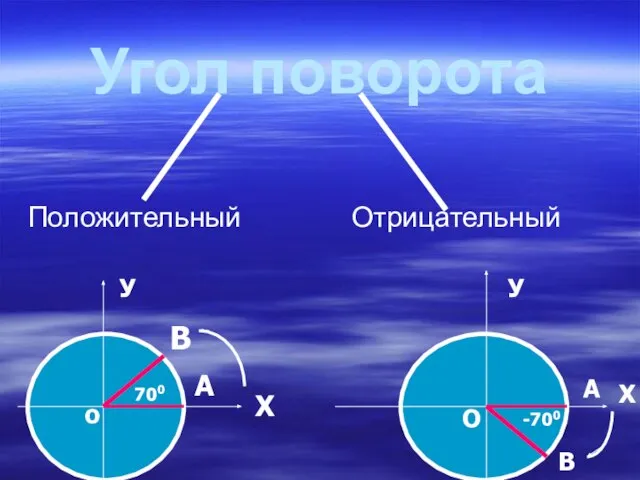
- 13. Угол поворота Положительный Отрицательный В А А В 700 -700 Х У У Х o O
- 14. Из курса геометрии известно: Мера угла в градусах выражается числом от 00 до 1800
- 15. Ответь на вопрос: Каким числом может выражаться в градусах угол поворота?
- 16. В Ы В О Д: Угол поворота может выражаться в градусах каким угодно действительным числом от
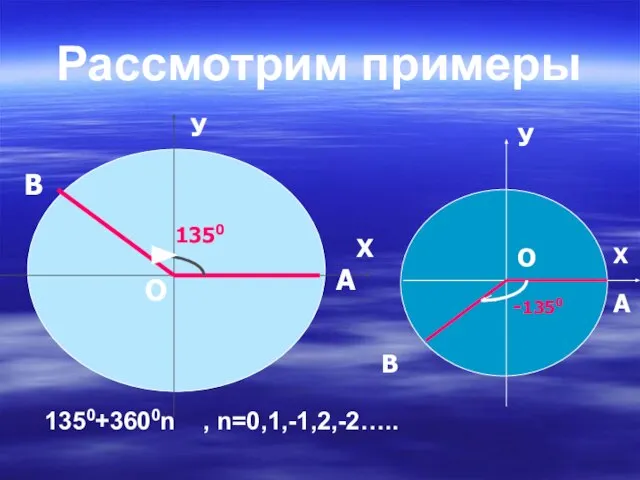
- 17. Рассмотрим примеры 1350+3600n , n=0,1,-1,2,-2….. 1350 Х У У Х -1350 А В О В О
- 18. В Ы В О Д Существует бесконечно много углов поворота, при которых начальный радиус ОА переходит
- 19. З А П О М Н И 00 900 1800 2700
- 20. В ы в о д: Эти углы не относятся ни к какой четверти. 00 ,± 900
- 21. Углом какой четверти является угол β,если: β=1670 β=2870 β=-650
- 22. Стр.153.- определение. y X Sinα= Cos= R R y X tgα= ctgα= X y
- 23. Лабораторная работа
- 24. В Ы В О Д: Синус, косинус, тангенс и котангенс не зависят от радиуса. Вычертите три
- 25. Запомни Sinα, Cosα-определены при любом α. Почему?
- 26. Стр.154 При каком α tgα не определён? Почему?
- 27. sinα , cosα , tgα , ctgα –называют тригонометрическими функциями.
- 28. Для единичной окружности: Область значения синуса и косинуса есть промежуток [-1;1] Область значения тангенса и котангенса
- 29. Найти синус, косинус,тангенс и котангенс 2700 Проверьте решение на стр.156
- 30. Устно № 699 №701
- 32. Скачать презентацию




















![Для единичной окружности: Область значения синуса и косинуса есть промежуток [-1;1] Область](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/310893/slide-27.jpg)


 В мире плоскостей
В мире плоскостей Смежные и вертикальные углы
Смежные и вертикальные углы Двугранный угол (10-11 класс) - презентация по Геометрии_
Двугранный угол (10-11 класс) - презентация по Геометрии_ Смотр общественных знаний
Смотр общественных знаний Урок 7 (8) Параллельность прямой и плоскости. Решение задач
Урок 7 (8) Параллельность прямой и плоскости. Решение задач Удивительный квадрат (10 класс)
Удивительный квадрат (10 класс) Параллелепипед
Параллелепипед Изображение пространственных фигур Мячина Екатерина Колдаева Есения 11 Г класс
Изображение пространственных фигур Мячина Екатерина Колдаева Есения 11 Г класс Координаты вектора
Координаты вектора Логические законы и правила
Логические законы и правила Признаки равенства треугольников 7 класс
Признаки равенства треугольников 7 класс Призма 9 класс
Призма 9 класс Основные формулы тригонометрии
Основные формулы тригонометрии Соотношения между сторонами и углами прямоугольного треугольника 8 класс - презентация________________________________________________________________________________
Соотношения между сторонами и углами прямоугольного треугольника 8 класс - презентация________________________________________________________________________________ ГИА 2013 Модуль «Геометрия» № 9
ГИА 2013 Модуль «Геометрия» № 9 Объемные тела. Пирамиды
Объемные тела. Пирамиды Геометрия крестово-купольного храма
Геометрия крестово-купольного храма Объем тел вращения - презентация по Геометрии
Объем тел вращения - презентация по Геометрии Учитель Лемешкина А.М.
Учитель Лемешкина А.М. Лабораторный практикум по геометрии 7 класс
Лабораторный практикум по геометрии 7 класс Многогранники: виды задач и методы их решения (типовые задания С2) - 1
Многогранники: виды задач и методы их решения (типовые задания С2) - 1 Прямоугольник, ромб, квадрат Задания для устного счета Упражнение 4 8 класс
Прямоугольник, ромб, квадрат Задания для устного счета Упражнение 4 8 класс Скрещивающиеся прямые. Углы с сонаправленными сторонами. Угол между прямыми
Скрещивающиеся прямые. Углы с сонаправленными сторонами. Угол между прямыми Теорема синусов 9 класс
Теорема синусов 9 класс Знакомство с миром геометрии
Знакомство с миром геометрии Геометрия 7 класс Геометрия 7 класс
Геометрия 7 класс Геометрия 7 класс Фракталы: наука и искусство XXI века
Фракталы: наука и искусство XXI века Объёмы и поверхности тел вращения
Объёмы и поверхности тел вращения