Содержание
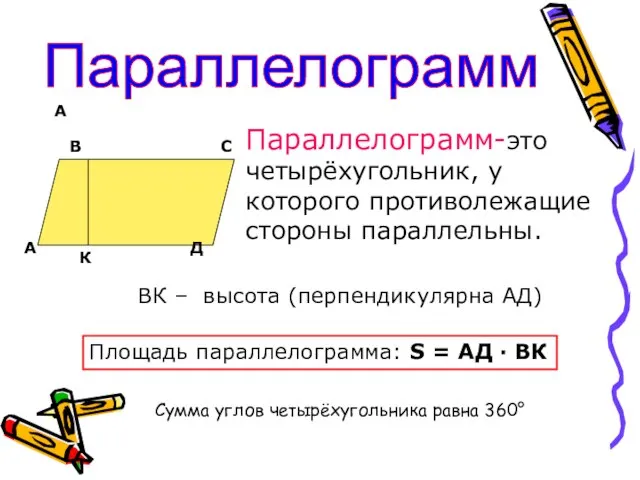
- 2. А Параллелограмм А В С Д К Параллелограмм-это четырёхугольник, у которого противолежащие стороны параллельны. ВК –
- 3. а Ромб а а d1 d2 Ромб – это параллелограмм, у которого все стороны равны d1,
- 4. а Прямоугольник а b Прямоугольник – это параллелограмм, у которого все углы прямые. Площадь прямоугольника: S
- 5. Квадрат а a Квадрат –это прямоугольник,у которого все стороны равны. Площадь квадрата: S = a ·
- 6. Трапеция – это четырёхугольник, у которого две противолежащие стороны параллельны, а две другие нет. Трапеция Трапеция
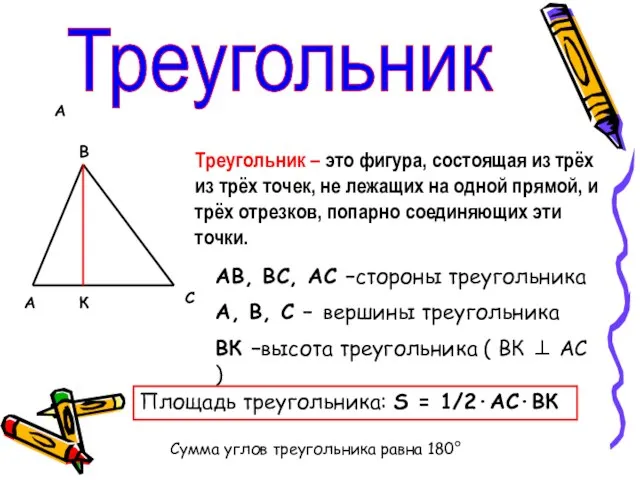
- 7. А Треугольник А В С К Треугольник – это фигура, состоящая из трёх из трёх точек,
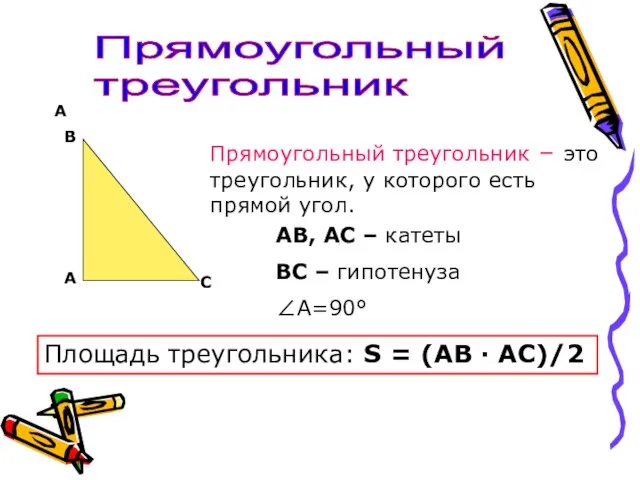
- 8. А Прямоугольный треугольник А В С Прямоугольный треугольник – это треугольник, у которого есть прямой угол.
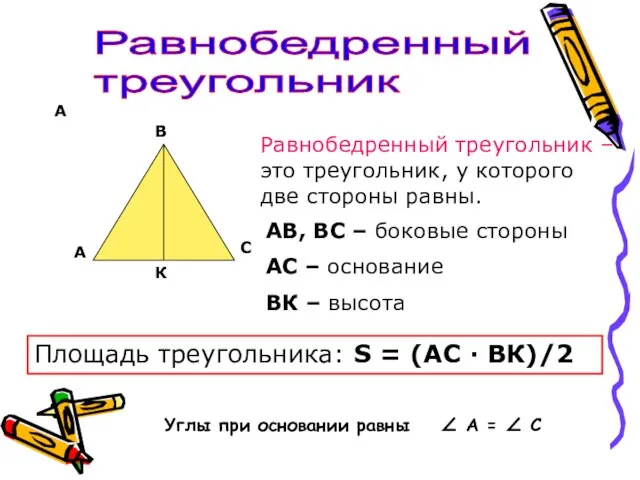
- 9. А Равнобедренный треугольник А В С К Равнобедренный треугольник –это треугольник, у которого две стороны равны.
- 11. Скачать презентацию




 Ромб
Ромб Геометрия.Введение. Аксиоматика.
Геометрия.Введение. Аксиоматика. Длина отрезка
Длина отрезка Параллельность в пространстве
Параллельность в пространстве Площадь круга и его частей
Площадь круга и его частей Теорема Фалеса 8 класс
Теорема Фалеса 8 класс Решение задач на применение признаков равенства треугольников
Решение задач на применение признаков равенства треугольников Графический способ решения систем укравнений
Графический способ решения систем укравнений Соотношения между сторонами и углами прямоугольного треугольника (Подготовка к контрольной работе)
Соотношения между сторонами и углами прямоугольного треугольника (Подготовка к контрольной работе) Пирамиды
Пирамиды Учитель математики МОУ СОШ № 4 им. Б. Машука г.Завитинска Амурской области. 2010-2011 уч. год.
Учитель математики МОУ СОШ № 4 им. Б. Машука г.Завитинска Амурской области. 2010-2011 уч. год. Площади плоских геометрических фигур
Площади плоских геометрических фигур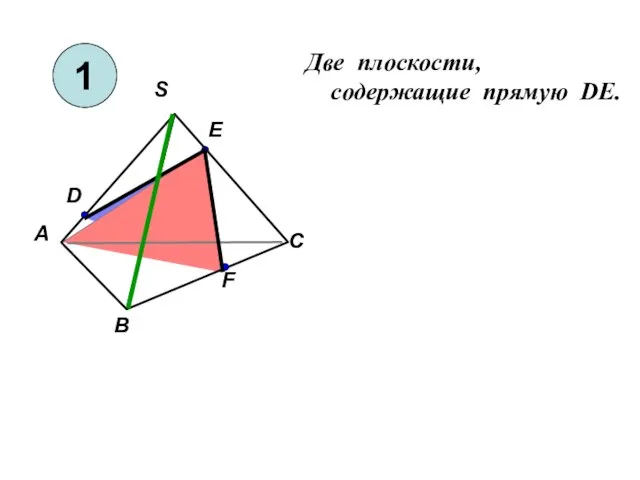 Две плоскости, cодержащие прямую DE
Две плоскости, cодержащие прямую DE Сечения прямоугольного параллелепипеда и тетраэдра
Сечения прямоугольного параллелепипеда и тетраэдра Площадь трапеции
Площадь трапеции Части фигур
Части фигур Измерение длин отрезков
Измерение длин отрезков Золотое сечение в геометрии - презентация по Геометрии_
Золотое сечение в геометрии - презентация по Геометрии_ Окружность в аксонометрии
Окружность в аксонометрии Перпендикулярность в пространстве (10 класс)
Перпендикулярность в пространстве (10 класс) Цилиндр и конус
Цилиндр и конус Сумма углов треугольника
Сумма углов треугольника Луч и угол (7 класс)
Луч и угол (7 класс) Азбука геометрической резьбы
Азбука геометрической резьбы Центральная симметрия
Центральная симметрия Проекция окружности в аксонометрии - презентация_
Проекция окружности в аксонометрии - презентация_ Что изучает геометрия 7 класс
Что изучает геометрия 7 класс Окружности
Окружности