Содержание
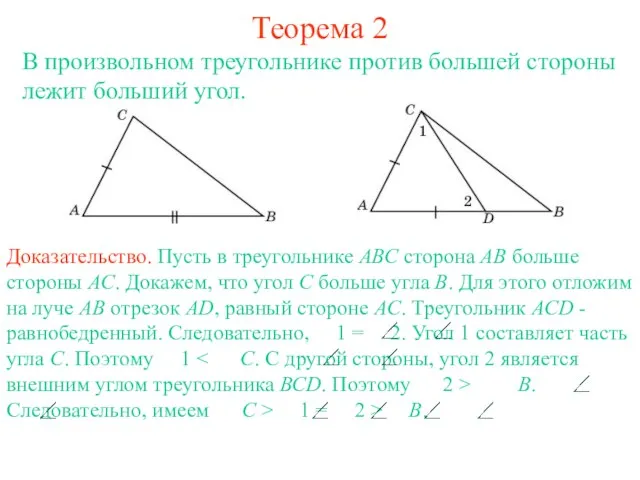
- 2. Теорема 2 В произвольном треугольнике против большей стороны лежит больший угол.
- 3. Упражнение 1 Может ли внешний угол треугольника равняться его внутреннему углу? Ответ: Да, в прямоугольном треугольнике.
- 4. Упражнение 2 Может ли внешний угол треугольника быть меньше его внутреннего угла? Ответ: Да, в тупоугольном
- 5. Упражнение 3 Сколько в треугольнике может быть: а) прямых углов; б) тупых углов? Ответ: а), б)
- 6. Упражнение 4 Известно, что в треугольнике ABC BC > AC >AB. Какой из углов больше: а)
- 7. Упражнение 5 В треугольнике ABC сторона AB наибольшая. Какие углы этого треугольника острые? Каким может быть
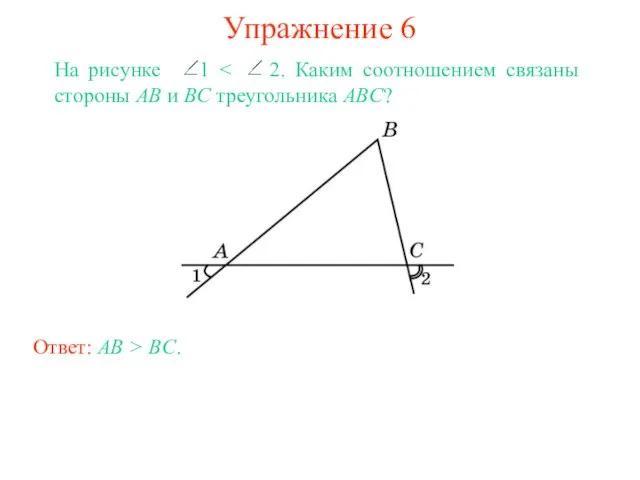
- 8. Упражнение 6 На рисунке 1 Ответ: AB > BC.
- 9. Упражнение 7 Верно ли, что в произвольном треугольнике против большего угла лежит большая сторона? Ответ: Да.
- 10. Упражнение 8 Ответ: а) BC > AC > AB; б) BC > AB, AC = AB.
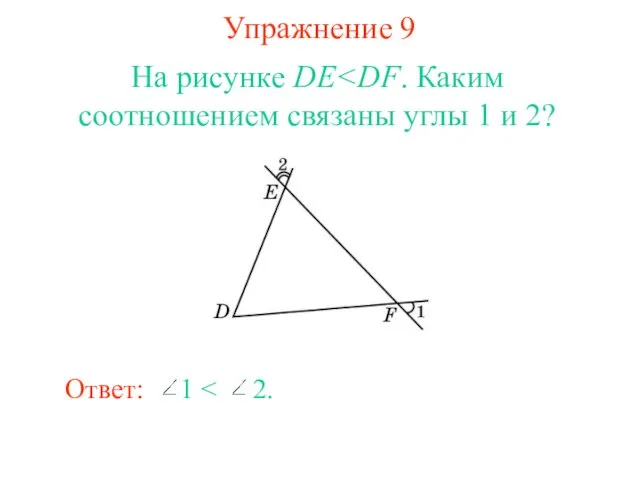
- 11. Упражнение 9 На рисунке DE
- 12. Упражнение 10 Какой вид имеет треугольник, если: а) два его угла равны; б) три его угла
- 13. Упражнение 11 Точка M лежит внутри треугольника ABC. Какой из углов больше BAC или BMC? Ответ:
- 15. Скачать презентацию









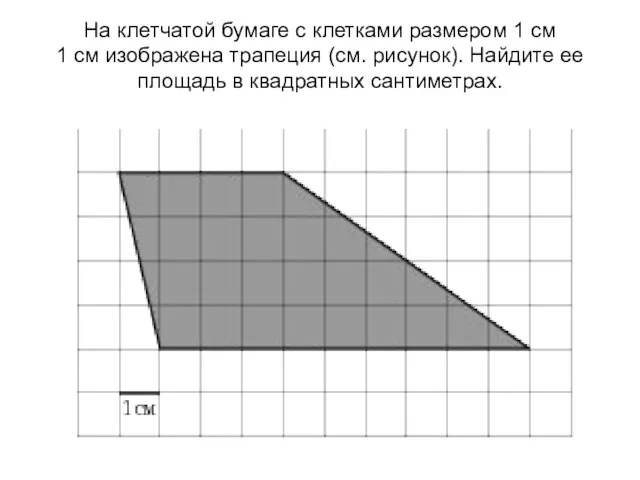 Площади фигур на клетке
Площади фигур на клетке Тетраэдр
Тетраэдр Формула Гириха
Формула Гириха Преобразование графиков функций - презентация по Геометрии__________________________________________________________________________________________________________________
Преобразование графиков функций - презентация по Геометрии__________________________________________________________________________________________________________________ Многоугольники
Многоугольники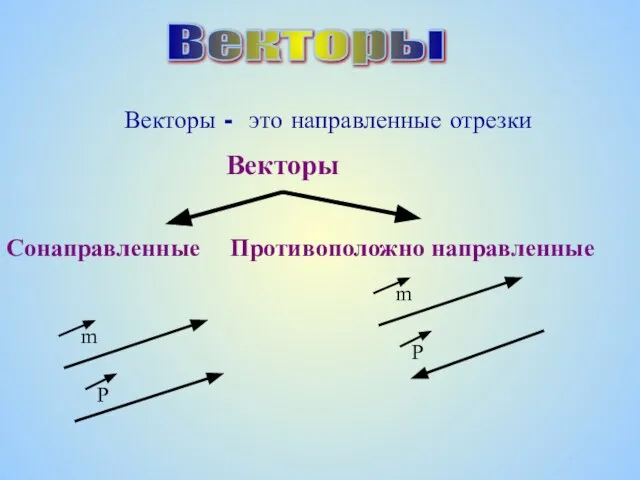 Векторы: Знакомство
Векторы: Знакомство Площади многоугольников
Площади многоугольников Измерение углов
Измерение углов Начертательная геометрия
Начертательная геометрия Что изучает геометрия 7 класс
Что изучает геометрия 7 класс Симметрия
Симметрия УСТНЫЕ ЗАДАЧИ ПО ТЕМЕ "ПРИЗМА"
УСТНЫЕ ЗАДАЧИ ПО ТЕМЕ "ПРИЗМА" Окружность и круг
Окружность и круг Решение задач на нахождение периметра и площади
Решение задач на нахождение периметра и площади Геометрические задачи на экстремум
Геометрические задачи на экстремум Подготовлю справочник по геометрии (или как повторить геометрию к экзамену)
Подготовлю справочник по геометрии (или как повторить геометрию к экзамену) Площадь многоугольника 8 класс
Площадь многоугольника 8 класс В мире треугольников
В мире треугольников Планиметрия
Планиметрия Измерение длин отрезков
Измерение длин отрезков Вводное повторение курса геометрии
Вводное повторение курса геометрии Правильная пирамида
Правильная пирамида Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда Площади плоских геометрических фигур
Площади плоских геометрических фигур Доклад о «Сфере и шаре»
Доклад о «Сфере и шаре» Сечения многогранников плоскостью
Сечения многогранников плоскостью Теорема синусов и косинусов в задачах с практическим содержанием
Теорема синусов и косинусов в задачах с практическим содержанием Симметрия правит миром
Симметрия правит миром