Слайд 2Цели и задачи.
1. Усвоение материала через практикум и теорию;
2. Формирование логического

мышления;
3. Научиться видеть различие и сходство в доказательствах признаков;
4. Пытаться развивать способности обучающихся к самообразованию;
5. Формирование умений саморегулирования своей учебно- познавательной деятельности.
Слайд 3Прямоугольные треугольники
Треугольник называется прямоугольным, если у него есть прямой угол. Сторона прямоугольного

треугольника, противолежащая прямому углу, называется гипотенузой, две другие стороны – катетами. AC и AB – катеты, BC – гипотенуза.
Теорема.
Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.
Слайд 4Прямоугольные треугольники
Доказательство.
Пусть ABC и A1B1C1 – данные треугольники. Построим треугольник DBC равный

треугольнику ABC, и треугольник D1B1C1 равный треугольнику A1B1C1.
Δ ABD = Δ A1B1D1 по третьему признаку равенства треугольников (AB=A1B1, BD=B1D1, AD=A1D1) из этого следует, что ∠ BAC = ∠ B1A1C1.
Δ ABC = Δ A1B1C1 по первому признаку равенства треугольников (AB=A1B1, AC=A1C1, Δ ABC = Δ A1B1C1). Теорема доказана.
Слайд 5Прямоугольные треугольники
2 признак равенства
если катет и прилежащий к нему острый угол

одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны.
Слайд 6Прямоугольные треугольники
ДАНО:
ΔABC, Δ A1B1C1
Угл C = Углу C1 = 90 °
AB =

A1B1
Доказать:
ΔABC= Δ A1B1C1
Слайд 7Прямоугольные треугольники
ДАНО:
ΔABC, ΔBDC
Угл A = Углу D = 90 °
Угл 1 =

Углу 2
Доказать:
ΔABC= Δ BDC
Слайд 8Прямоугольные треугольники
Найдите пары равных прямоугольных треугольников и докажите их равенство

Слайд 9Прямоугольные треугольники
ДАНО:
ΔABC
Угл 1 = Углу 2
Угл 3 = Углу 4
BD = DC
Доказать:

ΔABC – равнобедренный









 Смежные и вертикальные углы
Смежные и вертикальные углы Перпендикулярные прямые в пространстве
Перпендикулярные прямые в пространстве Площади фигур. Теорема Пифагора
Площади фигур. Теорема Пифагора Разные способы нахождения площади многоугольников
Разные способы нахождения площади многоугольников Определение параллельных прямых
Определение параллельных прямых Площадь 8 КЛАСС
Площадь 8 КЛАСС Решение задач по геометрии на готовых чертежах
Решение задач по геометрии на готовых чертежах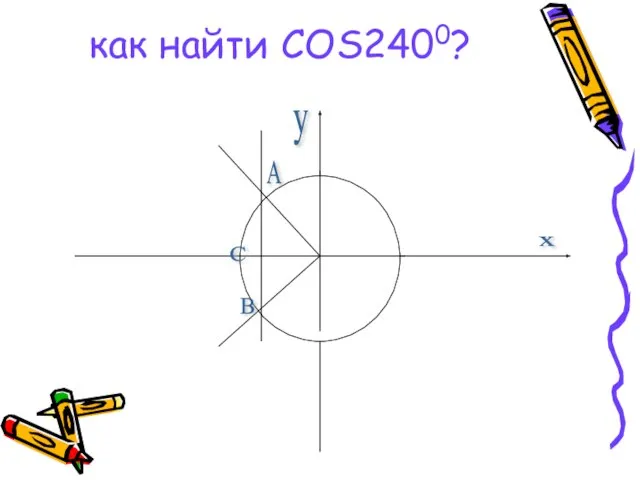 Косинус
Косинус Взаимное расположение графиков линейных функций
Взаимное расположение графиков линейных функций Учитель математики ГБОУ СОШ№1168 г. Москвы Мишина Раиса Михайловна
Учитель математики ГБОУ СОШ№1168 г. Москвы Мишина Раиса Михайловна Сопряжение. Геометрические построения - презентация по Геометрии_
Сопряжение. Геометрические построения - презентация по Геометрии_ Приращение функции и приращение аргумента
Приращение функции и приращение аргумента Биссектриса угла
Биссектриса угла Решение задач на вычисление площадей фигур
Решение задач на вычисление площадей фигур Двугранные углы - презентация по Геометрии_
Двугранные углы - презентация по Геометрии_ Построение геометрических тел
Построение геометрических тел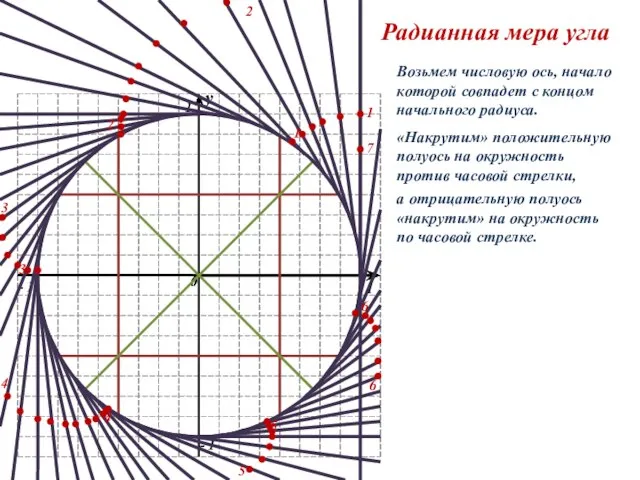 Радианная мера угла
Радианная мера угла Прямоугольник
Прямоугольник Координаты вектора
Координаты вектора Координатный метод
Координатный метод Скрещивающиеся прямые. Углы с сонаправленными сторонами. Угол между прямыми
Скрещивающиеся прямые. Углы с сонаправленными сторонами. Угол между прямыми Векторы
Векторы Векторы на плоскости и в пространстве, векторный метод решения задач
Векторы на плоскости и в пространстве, векторный метод решения задач Учитель математики МОУ СОШ № 4 им. Б. Машука г.Завитинска Амурской области. 2010-2011 уч. год.
Учитель математики МОУ СОШ № 4 им. Б. Машука г.Завитинска Амурской области. 2010-2011 уч. год. Простейшие задачи в координатах
Простейшие задачи в координатах Объём призмы
Объём призмы От египетского треугольника до Пифагора
От египетского треугольника до Пифагора Взаимное положение прямых Начертательная геометрия 11 класс
Взаимное положение прямых Начертательная геометрия 11 класс