Слайд 2Термодинамические методы анализа энергобалансов
Для оценки эффективности технологических систем и процессов используют материальные

балансы и энергетические балансы, базирующиеся на законах сохранения массы и энергии.
Энергетический баланс учитывает только количественные соотношения преобразования энергии, на основе которых определяется энергетический коэффициент полезного действия, но при этом не дается оценка количественного различия энергоресурсов различной физической природы и разного потенциала.
В связи с этим энергетические балансы дополняют эксергетическим балансом, основанном на одновременном учете первого и второго законов термодинамики.
Слайд 3Первый закон термодинамики
Для составления и анализа энергетических балансов может быть использован первый

закон термодинамики–частный случай закона сохранения энергии в применении к термическим процессам. Тепловая энергия Q, полученная системой, расходуется на увеличение внутренней энергии U системы и на совершение работы A.
Q=ΔU+A
При изобарном процессе полученная системой теплота расходуется на приращение энтальпии H
H=U+pV,
где р-давление, V-объем
Слайд 4Второй закон термодинамики
Второй закон термодинамики позволяет предсказывать принципиальную возможность и направление протекания

различных процессов и конечные состояния, которых они достигают. Для изолированной системы направление процесса определяется изменением энтропии S.
Дифференциал энтропии dS в обратимом процессе равен отношению приращения теплоты, полученного системой, к абсолютной температуре системы
dS=δQ/T
Для изолированной системы энтропия может только возрастать dS>0 и максимальна в состоянии равновесия dS=0
Максимальная полезная работа - эксергия теплоты Q - представляет собой работу равновесного цикла Карно
L=Q(1-Tu/Tz)
где Tu- температура окружающей среды, Tz- температура производства теплоты.
Слайд 5Эксергия
Энергия может быть представлена на T,s диаграмме как площадь фигуры, лежащей ниже
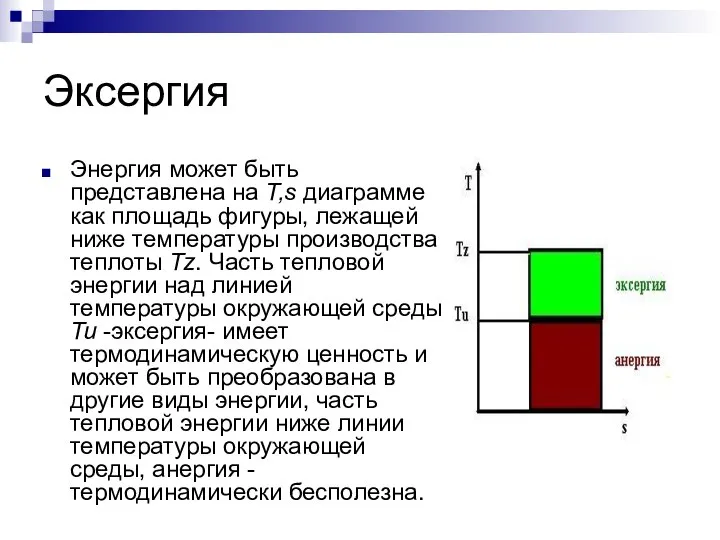
температуры производства теплоты Tz. Часть тепловой энергии над линией температуры окружающей среды Tu -эксергия- имеет термодинамическую ценность и может быть преобразована в другие виды энергии, часть тепловой энергии ниже линии температуры окружающей среды, анергия - термодинамически бесполезна.
Слайд 6Эксергетический баланс
Потеря работоспособности системы обусловлена рассеиванием энергии вследствие неравновесности процессов. Для эксергии

неприменим закон сохранения, сумма эксергий всех элементов системы в ходе процесса уменьшается. Уравнение Гюи-Стодолы позволяет определить эксергетические потери D
D=Tu ΔS,
где ΔS-изменение энтропии
Чем больше неравновесность процессов, тем меньше производимая системой работа.
Уравнение эксергетического баланса имеет вид
ΣE’= ΣE’’+D,
где ΣE’ и ΣE’’ -входящие и выходящие потоки эксергии, D -потери эксергии.





 Природные источники углеводородов. Природный и попутный нефтяные газы. Нефть. Каменный уголь
Природные источники углеводородов. Природный и попутный нефтяные газы. Нефть. Каменный уголь Способы разделение смесей. 7 класс
Способы разделение смесей. 7 класс Химиялық есептердің кеңістіктік шешімдері
Химиялық есептердің кеңістіктік шешімдері Фосфорні добрива. Технології збагачення фосфоровмісної сировини
Фосфорні добрива. Технології збагачення фосфоровмісної сировини Удивительный мир химических задач
Удивительный мир химических задач Спирты или алканолы
Спирты или алканолы KNO3 ; Ba(OH)2 ; Na2SO4 ; Al2(SO4)3 ;
KNO3 ; Ba(OH)2 ; Na2SO4 ; Al2(SO4)3 ;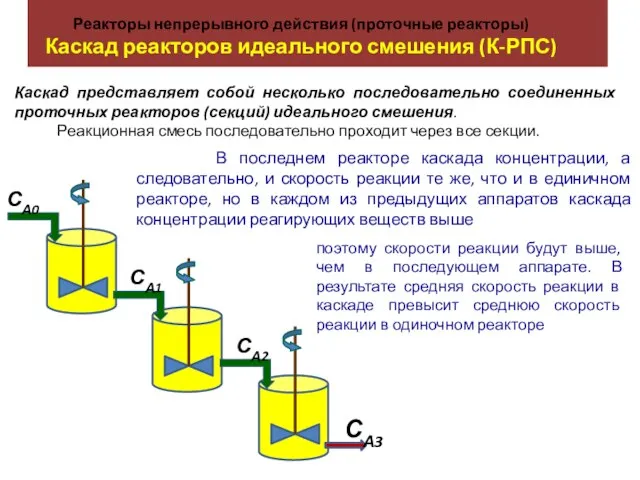 Реакторы непрерывного действия (проточные реакторы). Каскад реакторов идеального смешения (К-РПС)
Реакторы непрерывного действия (проточные реакторы). Каскад реакторов идеального смешения (К-РПС) Ионные двигатели
Ионные двигатели Периодический закон и Периодическая система химических элементов Д. И. Менделеева
Периодический закон и Периодическая система химических элементов Д. И. Менделеева Термокаталитические процессы переработки нефтяных фракций
Термокаталитические процессы переработки нефтяных фракций Введение Химия. Вещество. Свойства вещества
Введение Химия. Вещество. Свойства вещества Получение и примененипе радиоактивные изотопы
Получение и примененипе радиоактивные изотопы Презентация на тему Ковалентная неполярная связь
Презентация на тему Ковалентная неполярная связь  Свине́ц (Plumbum;Pb)
Свине́ц (Plumbum;Pb) Природный газ
Природный газ Генетичні зв’язки між неорганічними речовинами
Генетичні зв’язки між неорганічними речовинами Простые вещества металлы
Простые вещества металлы Презентация на тему Подготовка к ГИА по химии
Презентация на тему Подготовка к ГИА по химии  Сера. Характеристика химического элемента и простого вещества
Сера. Характеристика химического элемента и простого вещества Тема: «Первоначальные сведения о строении вещества»
Тема: «Первоначальные сведения о строении вещества» Бинарные соединения
Бинарные соединения Презентация на тему Щелочные и щелочноземельные металлы
Презентация на тему Щелочные и щелочноземельные металлы  Обобщение знаний об углеводородах
Обобщение знаний об углеводородах Основания, состав и классификация
Основания, состав и классификация Алкины. Ацетилен
Алкины. Ацетилен Термодинамика и теплопередача. Реальные газы
Термодинамика и теплопередача. Реальные газы Железо - основа всего мира
Железо - основа всего мира