Содержание
- 2. План Понятия: принцип, метод и методика анализа Этапы аналитических работ Основные метрологические характеристики
- 3. 1. Понятия: принцип, метод и методика анализа Принцип анализа – явление, свойство или закономерность, положенные в
- 4. Метод анализа – способ осуществления анализа. Например Методы количественного анализа: 1) химические (гравиметрия, титриметрия); 2) физико-химические
- 5. Методика анализа – алгоритм анализа. В методике в подробной форме оговаривается последовательность проведения анализа с целью
- 6. 2. Этапы аналитических работ Пробоотбор Пробоподготовка Измерение Обработка результатов анализа
- 7. 2. Этапы аналитических работ Пробоотбор Пробоотбор – процесс отбора пробы. Проба ‒ часть объекта исследования, отобранная
- 8. 2. Этапы аналитических работ Пробоотбор Проба, отобранная в какой-то одной точке участка, будет называться точечной. Точечная
- 9. 2. Этапы аналитических работ Пробоотбор Лабораторная проба – конечная проба, сокращенная генеральная проба, поступающая в лабораторию
- 10. 2. Этапы аналитических работ Пробоподготовка Пробоподготовка – подготовка пробы, совокупность действий, направленных на переведение пробы в
- 11. 2. Этапы аналитических работ Измерение Измерение величины – совокупность операций по применению технического средства, хранящего единицу
- 12. 2. Этапы аналитических работ Измерение Выбор метода анализа Необходимо представлять возможный диапазон определяемого содержания аналита в
- 13. 2. Этапы анализа. Измерение. Понятие ошибок в анализе Печалька! Истинное значение нам не узнать! К сожалению,
- 14. 3. Основные метрологические характеристики Метрология (от греч. μέτρον «мера» + λόγος «мысль; причина») – наука об
- 15. В связи с размером погрешности любой анализ имеет показатели, характеризующие качество измерений: правильность, воспроизводимость и точность.
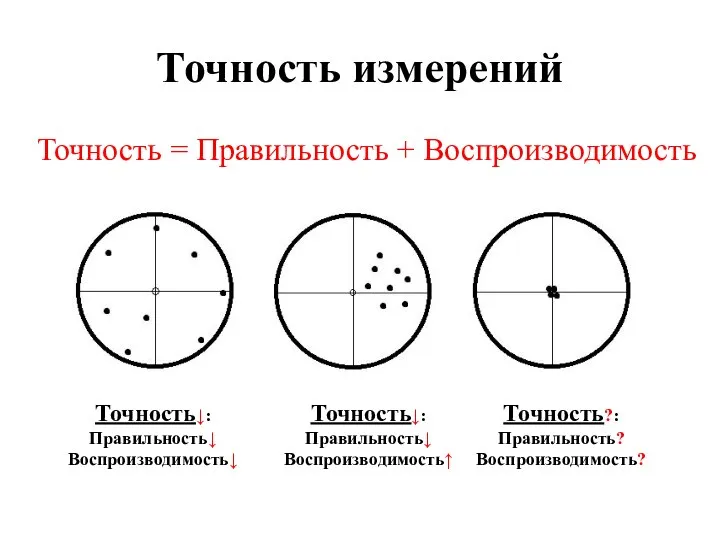
- 16. Точность измерений Точность = Правильность + Воспроизводимость Точность↓: Правильность↓ Воспроизводимость↓ Точность↓: Правильность↓ Воспроизводимость↑ Точность?: Правильность? Воспроизводимость?
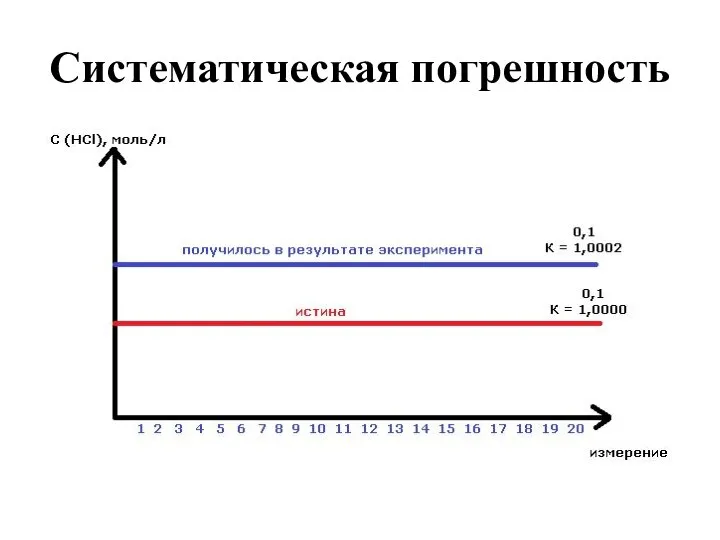
- 17. Погрешности измерения Систематические погрешности Систематической называют погрешность, которая при повторных измерениях остается постоянной или закономерно изменяется.
- 18. Систематическая погрешность
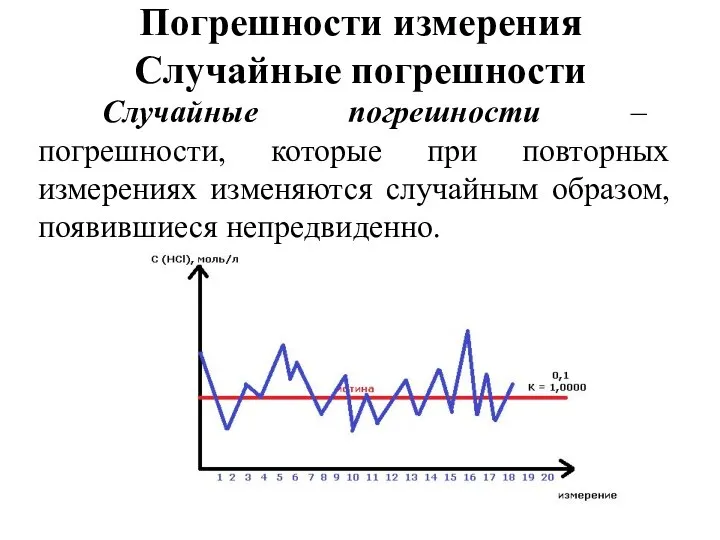
- 19. Погрешности измерения Случайные погрешности Случайные погрешности – погрешности, которые при повторных измерениях изменяются случайным образом, появившиеся
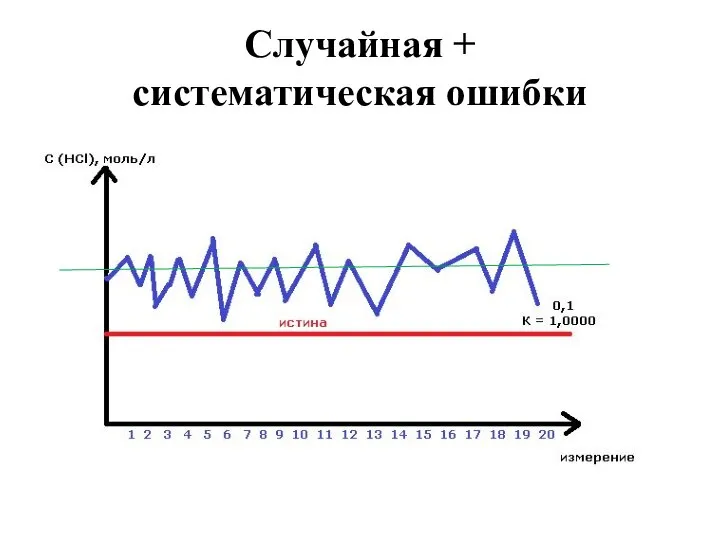
- 20. Случайная + систематическая ошибки
- 21. Грубая погрешность, или промах, — это погрешность результата отдельного измерения, входящего в ряд измерений, которая для
- 22. Погрешности измерений По способу числового выражения различают абсолютную и относительную погрешности
- 23. Погрешности измерений Абсолютная погрешность Абсолютная погрешность (∆хi) – разность между измеренным и истинным значением: ∆хi =
- 24. Погрешности измерения Относительная погрешность Отношение абсолютной погрешности измерения к истинному (опорному) значению измеряемой величины называется относительной
- 25. Алгоритм нахождения результата анализа с учетом случайной погрешности Из нескольких полученных единичных измерений находят среднее значение:
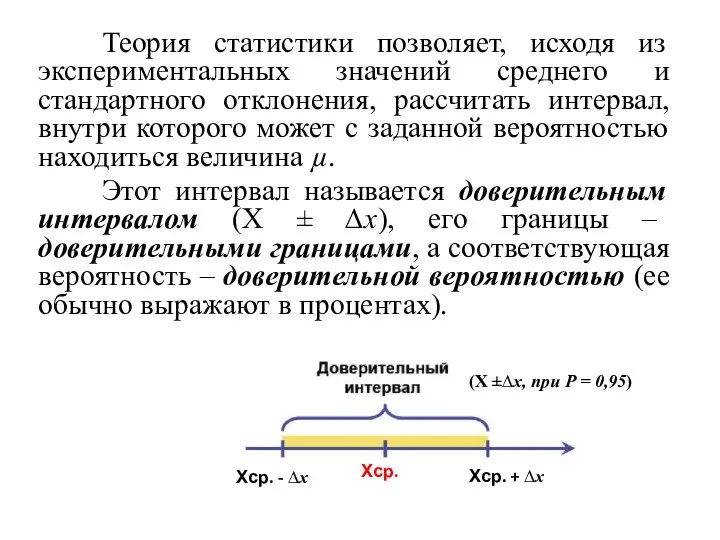
- 26. Теория статистики позволяет, исходя из экспериментальных значений среднего и стандартного отклонения, рассчитать интервал, внутри которого может
- 27. 3. Доверительный интервал рассчитывают по формуле: где t – статический коэффициент (коэффициент Стьюдента), величина которого зависит
- 28. 4. Результат анализа с учетом случайной погрешности записывают: Х = Хср. ± 5. Относительную погрешность анализа
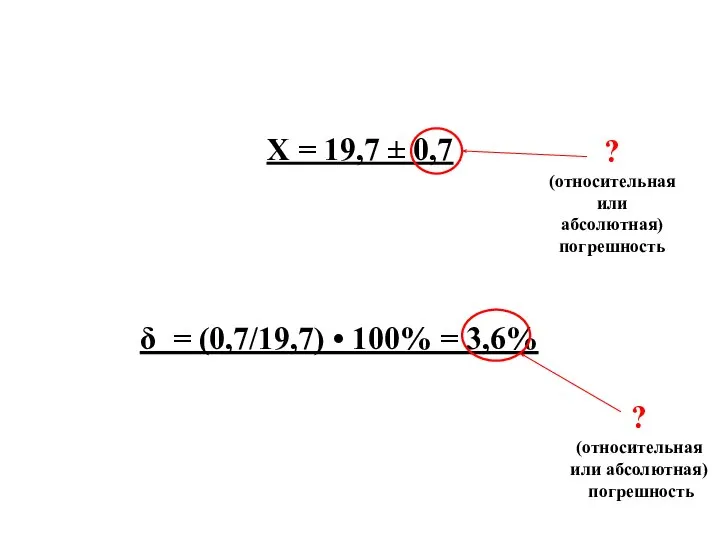
- 29. Пример обработки результатов анализа с учетом случайной погрешности Х = Хср. ± ΔХ Х = 19,7
- 30. Х = 19,7 ± 0,7 ? (относительная или абсолютная) погрешность . δ = (0,7/19,7) • 100%
- 32. Скачать презентацию























 Соли как производные кислот и оснований. Их состав и названия
Соли как производные кислот и оснований. Их состав и названия Предельные одноатомные спирты
Предельные одноатомные спирты Номенклатура и изомерия аренов
Номенклатура и изомерия аренов Итоговая консультация. Формульный диктант
Итоговая консультация. Формульный диктант Металлургия в химии
Металлургия в химии Химия дома
Химия дома Аттестационная работа. Многогранники: от молекулы до кристалла
Аттестационная работа. Многогранники: от молекулы до кристалла Нафта. Походження, переробка, використання
Нафта. Походження, переробка, використання Роль М.В Ломоносова и Дж.Дальтона в создании атомно-молекулярного учения.
Роль М.В Ломоносова и Дж.Дальтона в создании атомно-молекулярного учения. Сложные эфиры
Сложные эфиры Nanofibers of aluminum oxide
Nanofibers of aluminum oxide Образование химических связей
Образование химических связей Физико-химия поверхностных явлений в функционировании живых систем
Физико-химия поверхностных явлений в функционировании живых систем Фосфор в организме человека
Фосфор в организме человека Углерод. Характеристика элемента
Углерод. Характеристика элемента Металлы. Общая характеристика, химические свойства. Получение
Металлы. Общая характеристика, химические свойства. Получение Производство чугуна и стали
Производство чугуна и стали Электролитическая диссоциация
Электролитическая диссоциация Ионные уравнения реакций
Ионные уравнения реакций Морфологогия минералов
Морфологогия минералов Презентация на тему Аминокислоты
Презентация на тему Аминокислоты  Многоатомные спирты
Многоатомные спирты Метаболизм чужеродных соединений
Метаболизм чужеродных соединений Презентация на тему Производство серной кислоты
Презентация на тему Производство серной кислоты  Кислоты. Свойства кислот
Кислоты. Свойства кислот Теория растворов. (Тема 1.5)
Теория растворов. (Тема 1.5) Интерактивный плакат Алканы
Интерактивный плакат Алканы Алкины. Понятие об алкинах
Алкины. Понятие об алкинах