Физико-химическая механика и реология дисперсных структур. Лекция 15

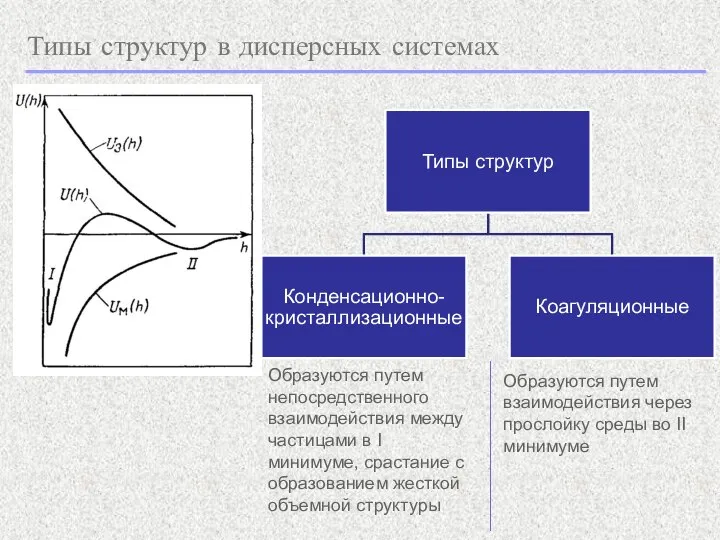
Типы структур в дисперсных системах
Образуются путем непосредственного взаимодействия между частицами в I минимуме, срастание с образованием жесткой объемной структуры
Образуются путем взаимодействия через прослойку среды во II минимуме

Типы структур в дисперсных системах

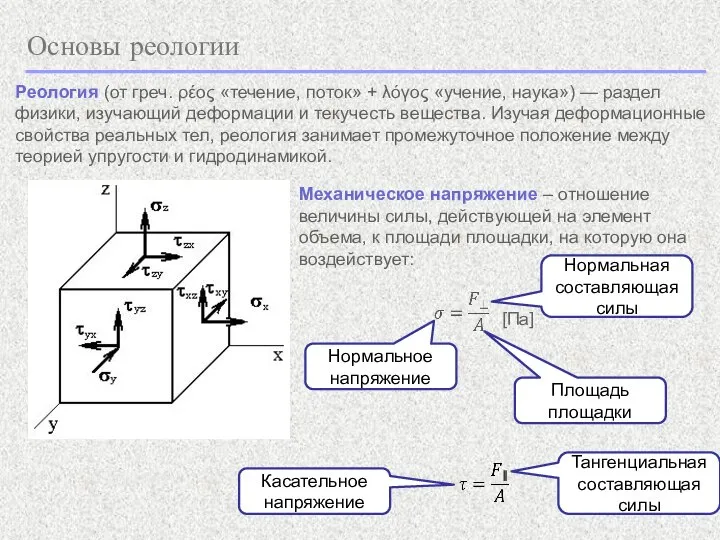
Основы реологии
Реология (от греч. ρέος «течение, поток» + λόγος «учение, наука») — раздел физики, изучающий деформации и текучесть вещества. Изучая деформационные свойства реальных тел, реология занимает промежуточное положение между теорией упругости и гидродинамикой.
Механическое напряжение – отношение величины силы, действующей на элемент объема, к площади площадки, на которую она воздействует:
Нормальное напряжение
Нормальная составляющая силы
Площадь площадки
Касательное напряжение
Тангенциальная составляющая силы
[Па]

Основы реологии
Результат воздействия внешних сил на тело: перемещение тела в пространстве как целого, либо изменение его формы (деформация).
Деформация – изменение расстояния между различными точками в объеме тела без утраты им сплошности.
Аксиомы реологии:
При всестороннем изотропном сжатии все тела ведут себя одинаково как идеально упругие тела;
Любая материальная система обладает всеми реологическими свойствами (упругость, пластичность, вязкость и прочность), которые проявляются в процессе деформирования.
Деформация при растяжении
- коэффициент Пуассона
Модуль Юнга [Па]
Для коры пробкового дерева
Для каучуков

Основы реологии
Деформация при сдвиге
Модуль сдвига

Закон Ньютона
Закон Ньютона для вязкости: при сдвиговом течении напряжение сдвига прямо пропорционально скорости сдвига, причем коэффициент пропорциональности называется вязкостью системы:
Динамическая вязкость [Па с]
Несистемная единица измерения динамической вязкости – Пуаз (Пз)
1 сПз = 1 мПа с
Кинематическая вязкость:

Шкала вязкости

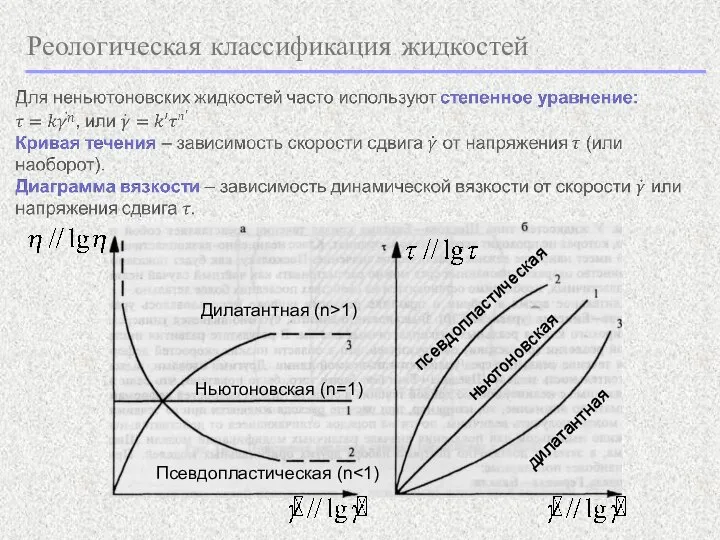
Реологическая классификация жидкостей

Реологическая классификация жидкостей
Дилатантная жидкость: вязкость растет с увеличением напряжения или скорости сдвига.
Псевдопластическая жидкость: вязкость падает с увеличением напряжения или скорости сдвига.
Нестационарные жидкости (есть зависимость вязкости от времени деформирования):
Тиксотропия – вязкость падает в процессе деформирования;
Реопексия – вязкость растет в процессе деформирования;
Зависимость вязкости от времени деформирования – признак перестройки (структурирования) в системе

Механические модели
Основные элементы механических моделей
Элемент Сен-Венана – Кулона.

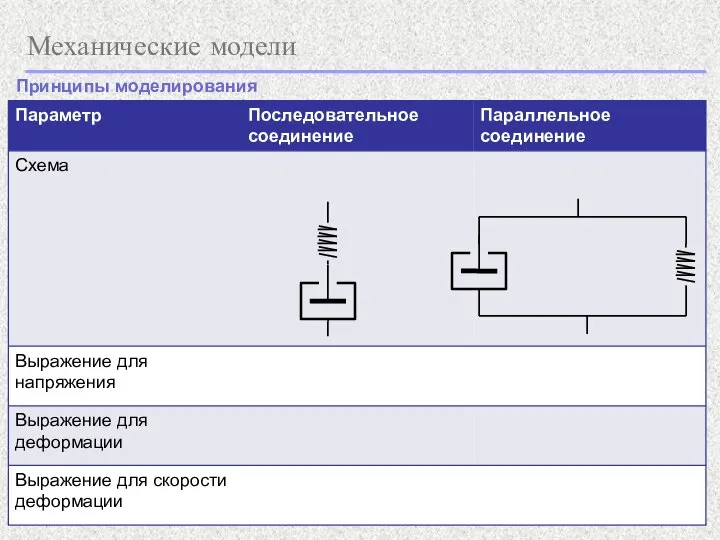
Механические модели
Принципы моделирования

Механические модели
Модель упруго-вязкого тела Максвелла (модель релаксирующей среды)

Механические модели
Модель Кельвина - Фойгта

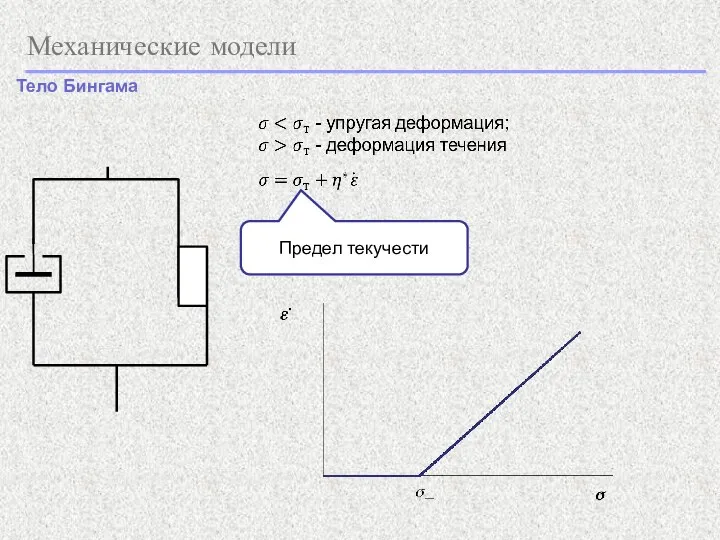
Механические модели
Тело Бингама
Предел текучести

Вязкость разбавленных дисперсий
Модельные предположения:
Система – достаточно разбавленная;
Нет взаимодействия между частицами дисперсной фазы;
Нет скольжения при смещении твердой поверхности относительно жидкости.
- уравнение Эйнштейна
Вязкость дисперсионной среды
Объемная доля дисперсной фазы
Для сферических частиц (иначе – коэффициент формы)
В уравнении Эйнштейна вязкость не зависит от размеров частиц!!! Однако в реальных системах эта зависимость есть. Объемная доля должна включать сольватную оболочку, адсорбционный слой, что более значимо для мелких частиц

Вязкость растворов
Выражения для вязкости растворов:
Относительная:
Удельная:
Приведенная:
Характеристическая:
[дл/г]
[дл/г]
[-]
[-]

Вязкость растворов полимеров
Молекулярная масса полимера

Температурная зависимость вязкости
Факторы: свободный объем и энергия кинетических единиц
Уравнение Аррениуса (Аррениуса – Френкеля – Эйринга, АФЭ):
Энергия активации
Слабо зависит от Т
Уравнение Вильямса – Ландела – Ферри:
Работает при

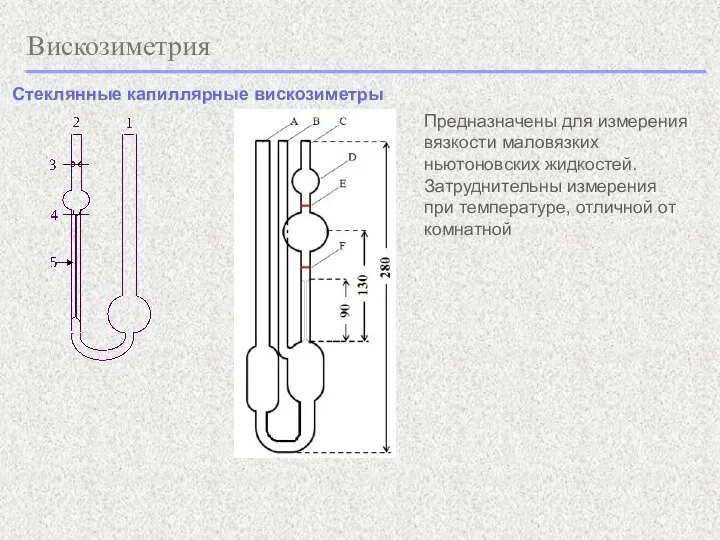
Вискозиметрия
Стеклянные капиллярные вискозиметры
Предназначены для измерения вязкости маловязких ньютоновских жидкостей. Затруднительны измерения при температуре, отличной от комнатной

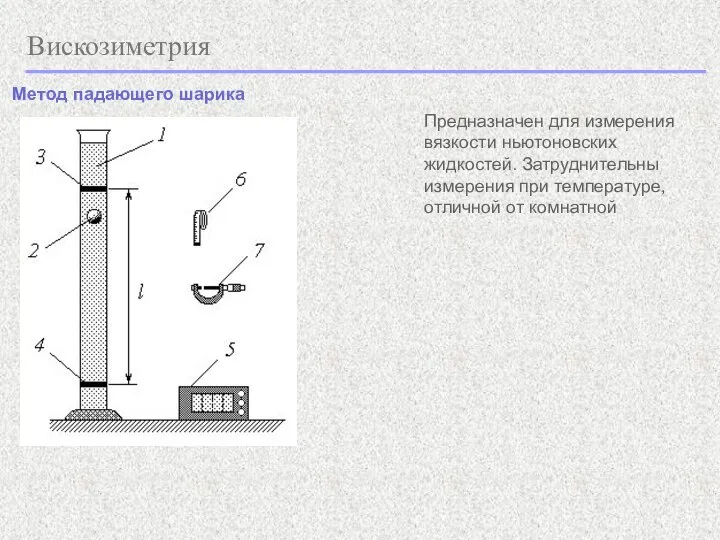
Вискозиметрия
Метод падающего шарика
Предназначен для измерения вязкости ньютоновских жидкостей. Затруднительны измерения при температуре, отличной от комнатной

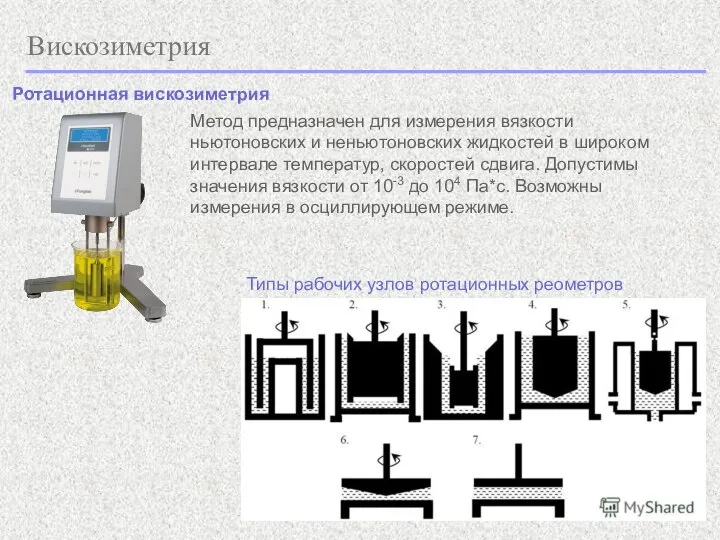
Вискозиметрия
Ротационная вискозиметрия
Метод предназначен для измерения вязкости ньютоновских и неньютоновских жидкостей в широком интервале температур, скоростей сдвига. Допустимы значения вязкости от 10-3 до 104 Па*с. Возможны измерения в осциллирующем режиме.
Типы рабочих узлов ротационных реометров