Физико-химические основы получения лекарственных препаратов

Основные понятия термодинамики фазовых равновесий
Термодинамическая система – отдельное тело или группа тел, находящихся во взаимодействии, и отделённых реальной или воображаемой границей от окружающей среды.
Фаза — это совокупность гомогенных частей системы, ограниченных поверхностью раздела и имеющих одинаковые химические, физические и термодинамические характеристики во всех своих точках.
Для образования разных фаз достаточно присутствия в системе одного вещества в разных агрегатных состояниях.
Газообразное, жидкое и твердое агрегатные состояния одного вещества отличаются по своим физическим (плотность, теплоемкость) и термодинамическим (ΔНообр, ΔSообр и т.д.) параметрам.

Основные понятия термодинамики фазовых равновесий
Пример однокомпонентной двухфазной системы — кусочки льда в воде.
Включение в систему водяного пара над поверхностью позволяет получить трехфазную однокомпонентную систему.
Фазовое превращение - переход вещества из одного агрегатного состояния в другое.
Одну и ту же фазу могут образовывать несколько разных веществ, когда вещества взаимно растворены друг в друге (например, хорошо смешивающиеся жидкости), или раствор каких-то веществ в некотором растворителе.
Истинный раствор — это однофазная система.

Основные понятия термодинамики фазовых равновесий
Разные вещества образуют в системе разные фазы.
а) Пример — смесь воды и масла состоит из двух жидких фаз. Фазы различаются не только по физическим и термодинамическим, но и по химическим характеристикам.
б) Если добавить в эту систему и третий компонент — например, раздробленный уголь, образуется третья фаза — твердая. В примере число фаз совпадает с числом компонентов.
В общем случае, количество фаз в системе может не совпадать с количеством компонентов.

Основные понятия термодинамики фазовых равновесий
Ф - число фаз.
Системы, состоящие из одной фазы (Ф = 1), называются гомогенными, а из нескольких фаз (Ф ≥ 2) — гетерогенными.
б) Фаза может быть непрерывной
дисперсной, т. е. состоять из отдельных фрагментов или частиц. Примеры дисперсных фаз —капельки масла в воде; пузырьки воздуха, появляющиеся в воде при нагревании; частицы измельченного угля; пыль в воздухе и т. д.
Дисперсная фаза распределена во второй — непрерывной фазе – дисперсионной среде.
По числу фаз системы делят на одно-, двух-, трёх- и многофазные.

Основные понятия термодинамики фазовых равновесий
Компонент – индивидуальное химическое вещество, являющееся составной частью системы, которое может быть выделено из неё и существовать самостоятельно.
Параметр системы - число независимых компонентов — К или число компонентов.
К — это наименьшее число индивидуальных химических веществ, необходимое для образования всех фаз термодинамической системы и для математического выражения состава всех фаз системы.
К = К0 – х,
где К0 - общее число компонентов в системе, х - число математических связей между характеристиками компонентов.

Основные понятия термодинамики фазовых равновесий
Таблица 1
По числу компонентов различают одно-, двух-, трёхкомпонентные и т.д. системы.

Условия фазового равновесия
Система находится в состоянии фазового равновесия относительно i-го компонента, если не происходит результирующего перемещения данного компонента из одной фазы в другую.
Рис. 1 Двухфазная система

Условия фазового равновесия
В гетерогенной системе имеется фазовое равновесие, если между фазами существуют следующие виды равновесий:
- термическое (температура во всех фазах системы одинакова),
- механическое (давление во всех фазах системы одинаково)
- и химическое (химический потенциал любого компонента во всех фазах системы одинаков) в отношении каждого компонента.

Условия фазового равновесия

ПРАВИЛО ФАЗ ГИББСА
Число термодинамических степеней свободы С равно числу компонентов К минус число фаз Ф плюс число n внешних факторов (температура, давление, различные силовые поля), влияющих на фазовое равновесие: С = К – Ф + n
Если число степеней свободы С = 0, то система - инвариантная (нонвариантная). Если С = 1, то система - моновариантная (одновариантная). Если С = 2, то система бивариантная (двухвариантная). Максимально возможное число фаз Фmax в равновесной системе реализуется в инвариантной системе при С = 0:

Уравнение Клаузиуса – Клапейрона

Уравнение Клаузиуса – Клапейрона

Уравнение Клаузиуса – Клапейрона

Диаграммы состояния однокомпонентных систем
К = 1. И положим п = 2, т. е. то, что из внешних параметров на систему влияют только температура и давление. Тогда правило фаз принимает вид:
C = 3 – Ф (4)
Ф = 1, то С = 2 — система имеет 2 степени свободы и называется бивариантной. Это значит можно произвольно менять 2 параметра — и давление, и температуру, — сохраняя то же фазовое состояние.
Ф = 2, то С = 1, т. е. система моновариантная. Для сохранения фазового равновесия произвольно можно менять либо Т, либо Р, а второй параметр должен принимать некоторое зависимое значение.
При определенной комбинации значений Т и Р одновременно сосуществуют три фазы: Ф = 3, С = 0. Система становится инвариантной. Изменение любого параметра выводит систему из такого состояния.

Диаграммы состояния однокомпонентных систем
Из выражения (4) следует: поскольку С не может быть отрицательным, то в однокомпонентной системе не может одновременно присутствовать больше трех фаз.
Диаграмма состояния воды
Диаграммы состояния производят в координатах давление – температура. Комбинация каких-либо значений Р и Т дает на диаграмме фигуративную точку, которой соответствует то или иное состояние системы.

Диаграмма состояния воды
Ключевое значение имеют три линии, разделяющие диаграмму на три области. Каждая из областей означает, что вода находится только в одном состоянии — жидком (Ж), твердом (Тв) или газообразном (Г).
б) Линии, разделяющие области, — это двухфазные состояния системы, т.е. при значениях Т и Р, отвечающих этим линиям, под поршнем существуют две фазы — именно те, области которых разделены соответствующей линией. Например, линия ОС разделяет области Ж и Г. Соответственно, на данной линии имеются сразу жидкая и газообразная фазы.
в) О точка пересечения всех трех линий, т. е. точка, где сходятся друг с другом все три области, называется тройной. При той паре значений Т и Р, которые соответствуют этой точке, под поршнем присутствуют сразу три фазы — Ж, Тв и Г

Диаграмма состояния воды
Такая диаграмма проясняет смысл результатов, вытекающих из правила фаз.
а) В пределах каждой области (где Ф = 1) можно менять одновременно оба параметра (и Т, и Р) — и мы будем оставаться внутри данной области, т. е. число и характер фаз будут неизменными.
Это и означает, что если Ф = 1, то С = 2 (система бивариантна).
б) На любой из разделительных линий (где Ф = 2) величины Т и Р уже связаны друг с другом. Чтобы оставаться на линии, относительно произвольно можно менять только один параметр, а второй должен изменяться зависимым образом.
Это иллюстрация того, что если Ф = 2, то С = 1 (система моновариантна).
в) И, наконец, сам термин «тройная точка» (где Ф = 3) означает, что нельзя изменить ни одного параметра, чтобы не выйти из этой точки (из трехфазного состояния системы). То есть, если Ф = 3, то С = 0 (система нонвариантна).

Физический смысл диаграммы состояния воды
1. а) Линия ОС соответствует ситуации, когда внешнее давление Р (со стороны поршня) совпадает с давлением насыщенного пара над жидкой водой:
б) С увеличением температуры, как известно, давление насыщенного пара возрастает. Так что линия ОС – это фактически график зависимости давления насыщенного пара над жидкой водой от температуры:
2. Линия ОА. а) При температурах ниже нуля вода находится уже не в жидком, а в твердом состоянии (лед, снег). Но и лед тоже способен испаряться, минуя жидкое состояние.
Переход вещества из твердого состояния сразу в газообразное называется сублимацией, или возгонкой.
б) Так вот, на линии ОА внешнее давление Р совпадает с давлением насыщенного пара надо льдом. Это давление вновь зависит от температуры; следовательно, линия ОА — это зависимость вида

Физический смысл диаграммы состояния воды
3. а) Линия ОВ отражает равновесие в системе лед - вода. Как известно, при атмосферном давлении плавление льда происходит при 0°С. Это точка К на линии ОВ.
б) Однако температура плавления льда, хотя и очень слабо, зависит от внешнего давления в системе: Тпл = Ψ(Р).
А именно: при резком уменьшении давления Тпл немного увеличивается, что является одним из проявлений принципа Ле Шателье.
кривая ОВ отличается по своему характеру от кривой АО:
она (ОВ) отражает не зависимость Р от Т (давления насыщенного пара от температуры), а, наоборот, зависимость Т от Р (температуры плавления от давления).
Если фигуративная точка лежит левее кривой ОВ, то вся вода находится в виде льда, а если правее — вся вода в жидком состоянии.

Физический смысл диаграммы состояния воды
4. Точка О. Допустим, что, оставаясь на кривой ОВ (где твердая и жидкая фаза находятся в равновесии), мы сильно снижаем внешнее давление — до того момента, пока оно не сравняется с давлением насыщенного пара надо льдом и над водой. Тогда появится возможность для образования и третьей фазы: пар сможет приподнять поршень и создать свою фазу.
Данное состояние и описывается тройной точкой О. Ее координаты:

Диаграмма состояния серы
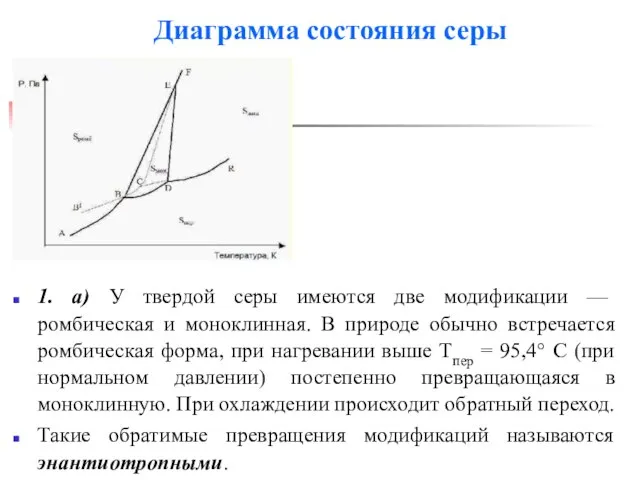
1. а) У твердой серы имеются две модификации — ромбическая и моноклинная. В природе обычно встречается ромбическая форма, при нагревании выше Tпер = 95,4° С (при нормальном давлении) постепенно превращающаяся в моноклинную. При охлаждении происходит обратный переход.
Такие обратимые превращения модификаций называются энантиотропными.

Диаграмма состояния серы

Диаграмма состояния серы