Поляризуемость. Эллипсоид поляризуемости и симметрия молекулы

Тензор в системе главных осей поляризуемости молекул:
При этом проекции на главные
оси поляризуемости:
Средний дипольный момент:
В общем случае
- напряженность статического поля
тогда
Размерность:

Эллипсоид поляризуемости и симметрия молекулы
Для поля напряженности ε с модулем, равным 1, произвольно меняющимся по направлению:
= 1
После подстановки выражений для проекций ε
получаем эллипсоид поляризуемости
Операция симметрии, допускаемая ядерной конфигурацией молекулы,
не должна изменять ее эллипсоида поляризуемости

Энергия молекулы во внешнем электрическом поле
Энергия поворота для жесткого диполя:
где - угол между вектором диполя и направлением поля.
Энергия поляризации (деформации):
(средняя составляющая собственных моментов направлена по полю)
Полная энергия :

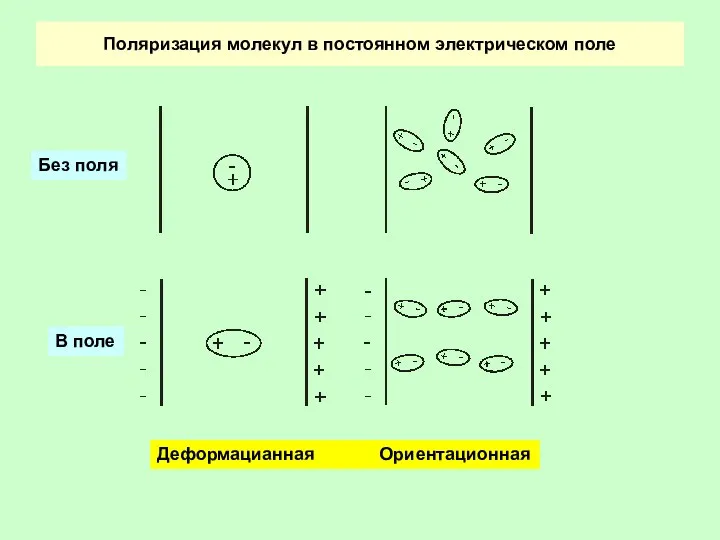
Поляризация молекул в постоянном электрическом поле
Деформацианная Ориентационная
Без поля
В поле

Ориентационная поляризация молекулы
Основные допущения:
1) плотность газа настолько низка, что энергия диполь-дипольного взаимодействия мала по сравнению с тепловой энергией (~kT);
2) поле ε не оказывает возмущающего действия на дипольный момент молекулы;
3) энергия молекулы в поле ε мала по сравнению со средней тепловой энергией молекулы.
Поляризация газа:
После усреднения:
Ориентационная поляризуемость молекулы:
В этом случае
Оценка вклада
для

Поляризация диэлектрика в переменном поле. Мольная рефракция
Диэлектрик в электрическом поле конденсатора:
Уравнение Клаузиуса-Моссотти для неполярных диэлектриков для которых
где
- число молекул в 1 м3.
(в традиционной форме)
Уравнение Ланжевена-Дебая:
(для полярных диэлектриков)
Уравнение Лоренца-Лоренца:
(для неполярных диэлектриков
в переменом электрическом поле
высокой частоты)
(b - электронная поляризуемость в переменном электрическом поле высокой частоты, n – показатель преломления, при экстраполяции к n∞ b стремится к статической электронной молярной поляризуемости αe )

Энергия образования молекул в классической теории
Для энергии образования моля вещества из свободных атомов:
Для энтальпий
Согласно классической теории:
Это выражение приводится к виду
Для моля молекул
и
– число связей в молекуле вида ( где I, J отражают валентное состояние и первое окружение каждого атома); – эффективная парциальная величина энергии образования, сопоставляемая связи этого вида.