Интеграл. Определенный интеграл. Свойства. Примеры. Применение определенного интеграла для нахождения длин, площадей и объемов

Определение интеграла
Интеграл - одно из важнейших понятий математического анализа, которое возникает при решении задач о нахождении площади под кривой, пройденного пути при неравномерном движении, массы неоднородного тела, и тому подобных, а также в задаче о восстановлении функции по её производной (неопределённый интеграл). Упрощённо интеграл можно представить как аналог суммы для бесконечного числа бесконечно малых слагаемых. В зависимости от пространства, на котором задана подынтегральная функция, интеграл может быть — двойной, тройной, криволинейный, поверхностный и так далее; также существуют разные подходы к определению интеграла — различают интегралы Римана, Лебега, Стилтьеса и другие

Понятие определенного интеграла
Пусть функция y = f(x) определена на отрезке [a, b], a < b. Выполним следующие операции:
1) разобьем [a, b] точками a = x0 < x1 < ... < xi-1 < xi < ... < xn = b на n частичных отрезков [x0, x1], [x1, x2], ..., [xi-1, xi ], ..., [xn-1, xn ];
2) в каждом из частичных отрезков [xi-1, xi ], i = 1, 2, ... n, выберем произвольную точку и вычислим значение функции в этой точке: f(zi);
3) найдем произведения f(zi) · Δxi, где – длина частичного отрезка [xi-1, xi ], i = 1, 2, ... n;
4) составим интегральную сумму функции y = f(x) на отрезке [a, b]:

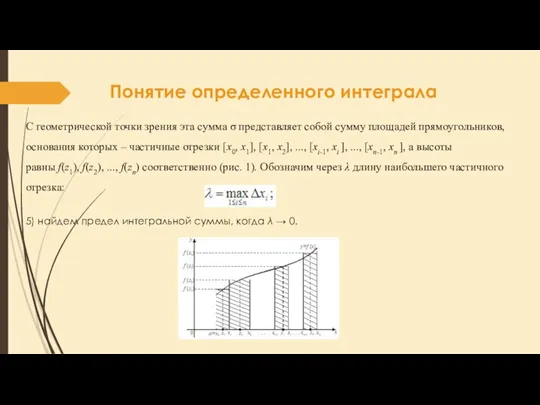
С геометрической точки зрения эта сумма σ представляет собой сумму площадей прямоугольников, основания которых – частичные отрезки [x0, x1], [x1, x2], ..., [xi-1, xi ], ..., [xn-1, xn ], а высоты равны f(z1), f(z2), ..., f(zn) соответственно (рис. 1). Обозначим через λ длину наибольшего частичного отрезка:
Понятие определенного интеграла
5) найдем предел интегральной суммы, когда λ → 0.

Понятие определенного интеграла
Определение. Если существует конечный предел интегральной суммы (1) и он не зависит ни от способа разбиения отрезка [a, b] на частичные отрезки, ни от выбора точек zi в них, то этот предел называется определенным интегралом от функции y = f(x) на отрезке [a, b] и обозначается
Таким образом,
В этом случае функция f(x) называется интегрируемой на [a, b]. Числа a и b называются соответственно нижним и верхним пределами интегрирования, f(x) – подынтегральной функцией, f(x)dx – подынтегральным выражением, x – переменной интегрирования; отрезок [a, b] называется промежутком интегрирования.

Понятие определенного интеграла
Теорема 1. Если функция y = f(x) непрерывна на отрезке [a, b], то она интегрируема на этом отрезке.
Определенный интеграл с одинаковыми пределами интегрирования равен нулю:
Если a > b, то, по определению, полагаем

Основные свойства определенного интеграла
1. Значение определенного интеграла не зависит от обозначения переменной интегрирования:
2. Постоянный множитель можно выносить за знак определенного интеграла:
3. Определенный интеграл от алгебраической суммы двух функций равен алгебраической сумме определенных интегралов от этих функций:

Основные свойства определенного интеграла
4. Если функция y = f(x) интегрируема на [a, b] и a < b < c, то
5. (теорема о среднем). Если функция y = f(x) непрерывна на отрезке [a, b], то на этом отрезке существует точка , такая, что

Пример решений
Пример 1
Вычислить определенный интеграл
Решение:
(1) Выносим константу за знак интеграла.
(2) Интегрируем по таблице с помощью самой популярной формулы
Появившуюся константу целесообразно отделить от и вынести за скобку.

Пример решений
(3) Используем формулу Ньютона-Лейбница
Сначала подставляем в верхний предел, затем – нижний предел. Проводим дальнейшие вычисления и получаем окончательный ответ.
Пример 2
Вычислить определенный интеграл
Решение:

Пример решений
(1) Используем свойства линейности определенного интеграла.
(2) Интегрируем по таблице, при этом все константы выносим – они не будут участвовать в подстановке верхнего и нижнего предела.
(3) Для каждого из трёх слагаемых применяем формулу Ньютона-Лейбница:

Вычисление длин дуг с помощью определённого интеграла
Если - параметрические уравнения гладкой кривой, то длина ее дуги равна , где и - производные функций
и соответственно, по параметру .
Существует аналогичная формула для длины дуги пространственной гладкой кривой:

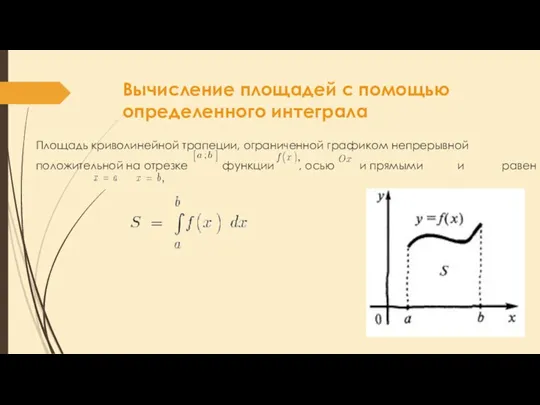
Вычисление площадей с помощью определенного интеграла
Площадь криволинейной трапеции, ограниченной графиком непрерывной положительной на отрезке функции , осью и прямыми и равен