Строение вещества

Задание 1. Электрические свойства и строение молекул
В таблице для t = 20°C приведены значения показателя преломления nD и плотности ρ раствора вещества А в веществе В с массовой долей растворенного вещества равной ω(A), и поляризация РA,∞ бесконечно разбавленного раствора вещества А в неполярном растворителе.
На основании данных таблицы, привлекая в необходимых случаях информацию из справочника [КС], определите:
а) удельную рефракцию раствора rA,B (м3/кг и см3/г);
б) удельную рефракцию чистого вещества В rB (м3/кг и см3/г), используя справочные данные о его показателе преломления и плотности [КС];
в) удельную рефракцию вещества А rA (м3/кг и смЗ/г) на основании правила аддитивности, исходя из количественного состава раствора ωA, значений удельной рефракции раствора rA,B и чистого вещества B rB;
г) молярную рефракцию вещества А (м3/моль и см3/моль), пользуясь значениями его молярной массы и удельной рефракции;
д) молярную рефракцию вещества А (м3/моль и см3/моль) по правилу аддитивности, исходя из предположений о возможном существовании у молекулы вещества A ИЗОМЕРОВ на основании справочных значений атомных рефракций и инкрементов рефракций связей [КС], а затем подтвердите или опровергните структуру молекулы вещества А;
е) момент электрического диполя вещества А (Кл∙м и Д) и сопоставьте его со справочными данными [КС]. приведите графические формулы всех возможных изомеров

Исходные данные
показатель преломления nD = 1,3481
плотность ρ = 1,0562 г/мл
Массовая доля ω = 12 % вещества А (CHOHCOOH)2 в веществе В (H2O) при 293 К
поляризация при бесконечном разведении вещества (CHOHCOOH)2 в неполярном растворе Р∞ = 250.491∙10-6 м3/моль

Удельную рефракцию H2O вычислим на основании показателя преломления и плотности из справочника по формуле
Используя свойство аддитивности удельной рефракции

Определим удельную рефракцию вещества А (м3/кг и см3/г), используя массовую долю:
Зная удельную рефракцию и молярные массы веществ А и B, вычислим значения молярной рефракции (см3/моль)

Графическая формула молекулы винной кислоты (CHOHCOOH)2 имеет вид:
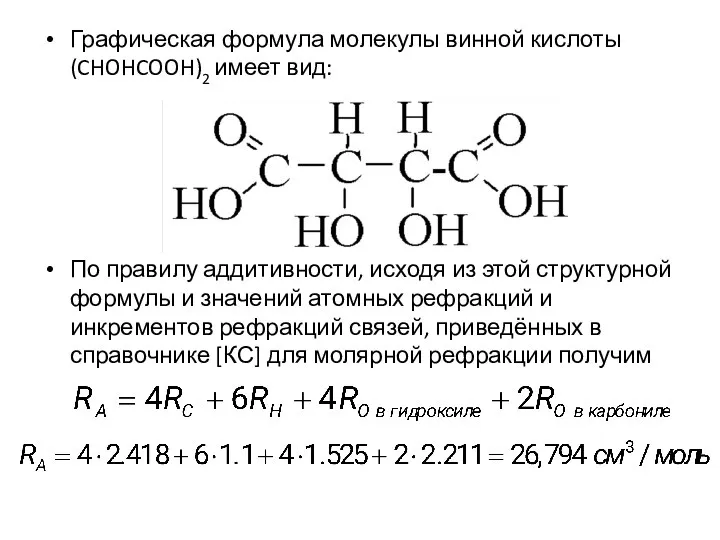
По правилу аддитивности, исходя из этой структурной формулы и значений атомных рефракций и инкрементов рефракций связей, приведённых в справочнике [КС] для молярной рефракции получим

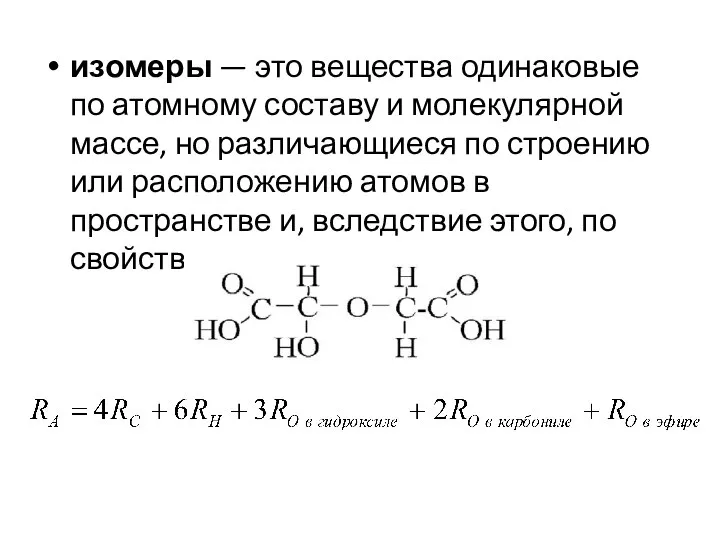
изомеры — это вещества одинаковые по атомному составу и молекулярной массе, но различающиеся по строению или расположению атомов в пространстве и, вследствие этого, по свойствам.

Момент электрического диполя вещества А в дебаях вычисляется по формуле:
Следует обратить внимание, что коэффициент 0,0128 в этой формуле получен путем объединения физических постоянных таким образом, что расчет по формуле даёт величину момента электрического диполя в дебаях при подстановке величин поляризации и рефракции в см3/моль :
Справочное значение момент электрического диполя по справочнику совпадает с рассчитанным.

Задание 2. Химическая связь
Запишите электронные конфигурации: 1) атомов A и B; 2) молекулы А–В (за основу примите энергетические уровни – молекулярные орбитали гомоядерных молекул)
Нарисуйте схематически энергетическую диаграмму молекулы А–В и распределите электроны на энергетических уровнях.
Установите, обладает ли: 1) вещество АВ диамагнитными или парамагнитными свойствами 2) молекула А–В электрическим диполем.
Как изменится: 1) энергия связи, если молекулу AB перевести в состояние иона AB+; 2) равновесное межъядерное расстояние, если молекулу AB перевести в состояние иона AB+; 3) энергия связи, если молекулу AB перевести в состояние иона AB-; 4) равновесное межъядерное расстояние, если молекулу AB перевести в состояние иона AB-.

1897 г Вехерт и Томсон – открытие электрона и расчет его массы ( 9,11.10-31 кг)
1902 г Томсон предложил теорию строения атома, согласно которой атомы представляют собой сферы, имеющие диаметр порядка нескольких ангстремов (1Å = 10-10 м), заполненные положительно заряженным веществом. В это вещество вкраплены электроны в таком количестве, чтобы атом в целом был электронейтральным (модель «пудинга с изюмом»).
1909 г Милликен – определение заряда 1,6.10-19 Кл
1911 г Э.Резерфорд предложил модель атома в виде положительно заряженного ядра малого объема, в котором сконцентрирована фактически вся масса, и электронов, вращающихся вокруг этого ядра по орбитам на различных расстояниях от него. Расположение электронов и ядер напоминало картину планет в солнечной системе, в результате модель получила название «планетарной».

1913 г Бор высказал утверждение, что в изолированном атоме электрон движется вокруг ядра, находящегося в центре атома, по стационарным орбитам, не излучая и не поглощая энергии.
Устойчивыми (разрешенными) для электрона будут только такие орбиты, на которых момент импульса электрона принимает значения, являющиеся строго кратными числу h/2π, где h – постоянная Планка (6,63·10-34 Дж·с).
В случае плоских круговых орбит условие квантования Бора выглядит следующим образом:
n – натуральное число
Радиус первой боровской орбиты (n = 1), принятый за атомную единицу длины а0, составляет 0,529 Å. Скорость движения электрона на первой боровской орбите в атоме водорода 2,19·106 м/с.

Ччтобы получить выражение для расчета энергии электрона на разрешенных боровских орбитах в атоме водорода, полную энергию этой системы Еполн следует представить в виде суммы кинетической и потенциальной энергий, которая составит:
Выделение (или поглощение) энергии происходит при переходе электрона с одной стационарной орбиты на другую. При этом изменение энергии ΔЕ равно одному кванту монохроматического электромагнитного излучения

Электрон их нельзя рассматривать в рамках классической механики, для электрона можно говорить лишь о его локализации в некоторой области пространства в определенный момент времени t.
Важнейшим понятием квантовой механики является понятие волновой функции Ψ, описывающей состояние системы микрочастиц.
Квадрат абсолютной величины (модуля) волновой функции пропорционален вероятности нахождения частицы в окрестности точки с координатами х, y, z в момент времени t. Там, где значение велико, велика и вероятность нахождения частицы, а там где оно мало, вероятность нахождения мала.

В 1926 году австрийский физик Э. Шредингер предложил ставшее фундаментальным в квантовой механике уравнение для определения волновых функций Ψ.
В результате решения уравнения Шредингера для связанных состояний электрона в атоме появляются константы n, l, ml, называемые главным, орбитальным и магнитным квантовыми числами

При построении электронных конфигураций следует учитывать:
принцип минимума энергии;
принцип (запрет) Паули (два и более тождественных электрона не могут одновременно находиться в одном и том же квантовом состоянии);
правило Хунда (Это означает, что в каждой из орбиталей подслоя заполняется сначала один электрон, а только после исчерпания незаполненных орбиталей на эту орбиталь добавляется второй электрон.).

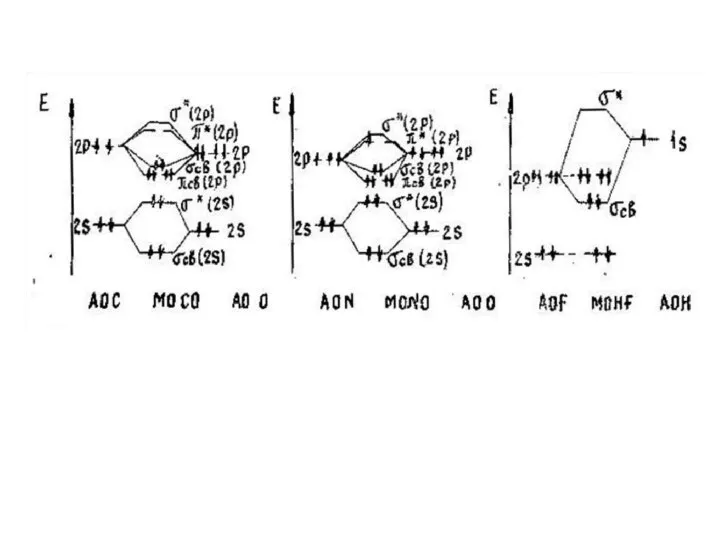
В методе МО предполагается, что состояние электронов в молекуле или ионе описывается одноэлектронными и волновыми функциями Ψi, охватывающими все ядра системы и называемыми молекулярными орбиталями.
Графическое изображение процесса сложения волновых функций заключается в следующем: граничная поверхность МО рассматривается как результирующая от перекрывания (наложения) граничных поверхностей отдельных АО.

Иллюстрация методов МО на молекуле водорода:
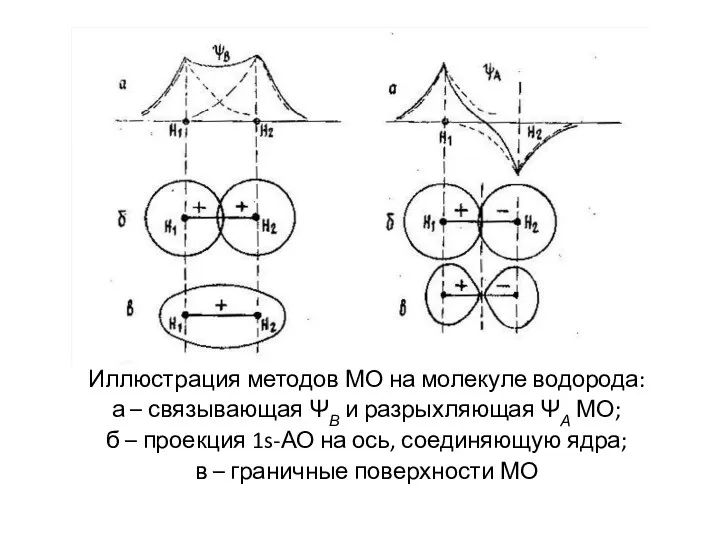
а – связывающая ΨВ и разрыхляющая ΨА МО;
б – проекция 1s-АО на ось, соединяющую ядра;
в – граничные поверхности МО

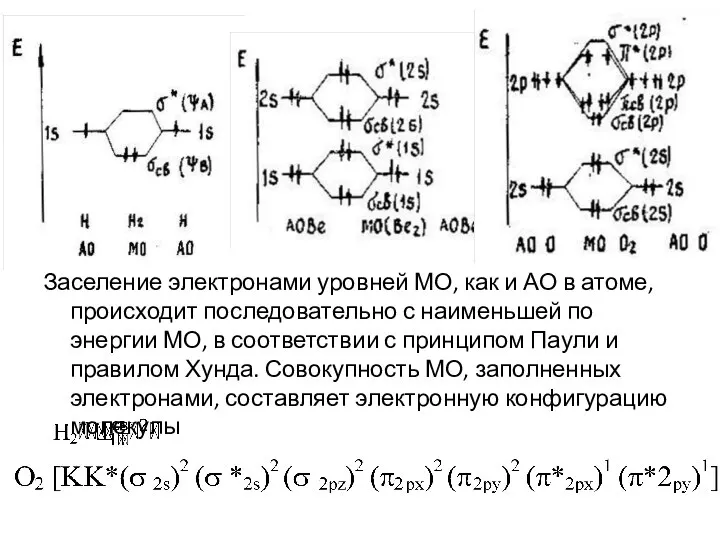
Заселение электронами уровней МО, как и АО в атоме, происходит последовательно с наименьшей по энергии МО, в соответствии с принципом Паули и правилом Хунда. Совокупность МО, заполненных электронами, составляет электронную конфигурацию молекулы

Рассмотрим молекулу О2.
Электронная конфигурация атома кислорода О [1s2 2s2 2p4].
На орбиталях молекулы O2 распределены 12 валентных электронов, значит, молекула имеет конфигурацию:
Молекула кислорода по методу валентных связей
не имеет неспаренных электронов и должна обладать
диамагнитными свойствами, что не согласуется с
экспериментальными данными.

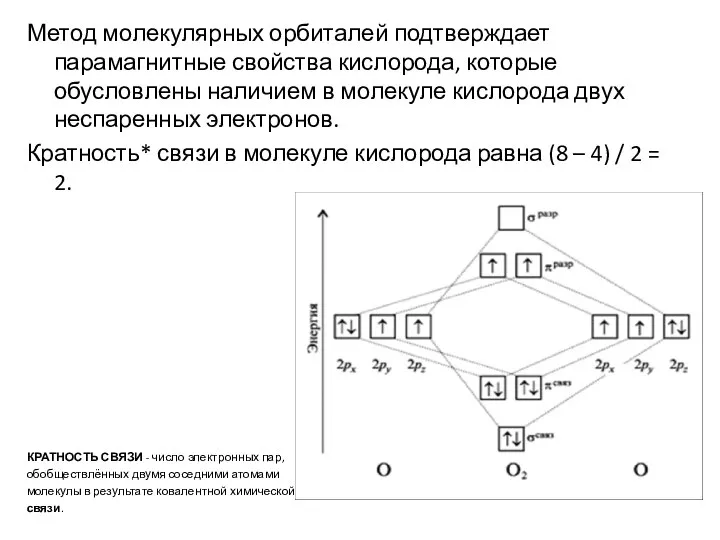
Метод молекулярных орбиталей подтверждает парамагнитные свойства кислорода, которые обусловлены наличием в молекуле кислорода двух неспаренных электронов.
Кратность* связи в молекуле кислорода равна (8 – 4) / 2 = 2.
КРАТНОСТЬ СВЯЗИ - число электронных пар,
обобществлённых двумя соседними атомами
молекулы в результате ковалентной химической
связи.

Рассмотрим электронное строение ионов O2+ и O2-.
В ионе O2+ на его орбиталях размещаются 11 электронов, следовательно, конфигурация иона следующая:
Кратность связи в ионе О2+ равна (8 – 3) / 2 = 2,5.
В ионе O2- на его орбиталях распределены 13 электронов. Этот ион имеет следующее строение:
Кратность связи в ионе О2- равна (8 – 5) / 2 = 1,5.
Ионы О2- и О2+ являются парамагнитными, так как содержат неспаренные электроны.

Задание 3. Вращательные спектры молекул
Выведите уравнения для: 1) расчета изменения энергии вращения двуатомной молекулы как жесткого ротатора при переходе ее на соседний, более высокий квантовый уровень энергии вращательного движения; 2) зависимости волнового числа вращательных линий в спектре поглощения двухатомной молекул от вращательного квантового числа; 3) расчета разности волновых чисел соседних линий во вращательном спектре поглощения двухатомной молекулы; 4) для вычисления равновесного межъядерного расстояния на основании значения разности волновых чисел соседних линий во вращательном спектр поглощения.
Вычертите схематически энергетические уровни вращательного движения двухатомной молекулы как жесткого ротатора. Как должны располагаться друг относительно друга вращательные квантовые уровни молекулы, не являющейся жестким ротатором? Нанесите пунктиром эти уровни на схему, вычерченную в предыдущем пункте. Нарисуйте схематически вращательный спектр поглощения двухатомной молекулы. Объясните причину немонотонного изменения интенсивности вращательных линий поглощения по мере увеличения энергии вращения молекулы.
На основании экспериментальных данных об изменении энергии вращения при переходе двухатомной молекулы А с третьего (j = 3) вращательного квантового уровня на четвертый (j = 4), определите: а) вращательную постоянную Ве (см-1); б) энергию вращения молекулы А на нулевом, первом, втором, третьем, четвертом и пятом вращательных уровнях (Дж); в) момент инерции молекулы А (кг·м2); г) равновесное межъядерное расстояние в молекуле А (нм); д) сопоставьте полученную величину со справочными данными [КС].

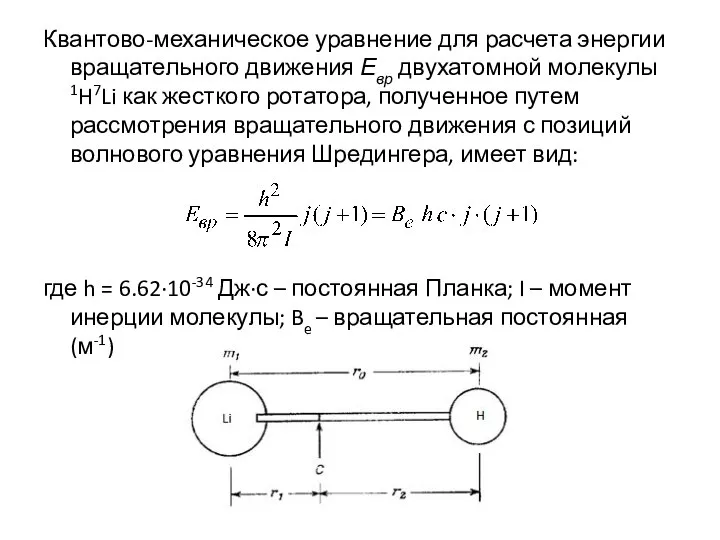
Квантово-механическое уравнение для расчета энергии вращательного движения Евр двухатомной молекулы 1H7Li как жесткого ротатора, полученное путем рассмотрения вращательного движения с позиций волнового уравнения Шредингера, имеет вид:
где h = 6.62∙10-34 Дж∙с – постоянная Планка; I – момент инерции молекулы; Be – вращательная постоянная (м-1)

Атомы массами m1и m2 связаны жестким стержнем (связью) длиной
Концы молекулы вращаются вокруг точки с — центра тяжести, положение которого определяется условием равновесия
Для двухатомной молекулы момент инерции вычисляется по формуле
где равновесное межъядерное расстояние re = const, поскольку молекула рассматривается как жесткий ротатор.

Переходы между уровнями определяются правилом отбора
Энергия перехода между двумя соседними уровнями равна
а поскольку j” = j’ + 1, то

Из уравнения следует, что зависимость волнового числа вращательных линий в спектре поглощения двухатомной молекулы вращательного квантового числа имеет вид:
В общем случае для перехода молекулы из состояния j в состояние (j + 1)
В общем случае для перехода молекулы из состояния j в состояние (j + 1) и из (j + 1) в (j + 2) разность волновых чисел соседних линий во вращательном спектре поглощения двухатомной молекулы будет

Уравнение для вычисления равновесного межъядерного расстояния на основании значения разности волновых чисел соседних линий во вращательном спектре поглощения
На основании экспериментальных данных об изменении энергии вращения при переходе молекулы c третьего (j = 3) на четвертый (j = 4) вращательный квантовый уровень определим вращательную постоянную Be (Дж, м-1 и см-1) молекулы 1Н7Li, для которой ΔEвращ = 119,440∙10-23 Дж, следовательно, получим

Определим энергию вращения молекулы 1Н7Li на нулевом, первом, втором и третьем вращательных квантовых уровнях (Дж)
Определим момент инерции молекулы 1H7Li (кг∙м2)