Содержание
- 2. Логика – это наука о формах и законах человеческого мышления.
- 3. Логика Джордж Буль (1815-1864). Создал новую область науки - Алгебру логики (Булеву алгебру или Алгебру высказываний).
- 4. Алгебра логики (булева алгебра) - это раздел математики, изучающий высказывания, и логические операции над ними. Цель
- 5. высказывания
- 6. Логическое высказывание – это повествовательное предложение, относительно которого можно однозначно сказать, истинно оно или ложно. Высказывание
- 7. Виды высказываний
- 8. Высказывание называется простым, если никакая его часть сама не является высказыванием. Сложные (составные) высказывания строятся из
- 9. Так, например, из элементарных высказываний "Петров — врач", "Петров — шахматист" при помощи связки "и" можно
- 10. При помощи связки "или" из этих же высказываний можно получить составное высказывание "Петров — врач или
- 11. В алгебре логики высказывания обозначают ЗАГЛАВНЫМИ буквами латинского алфавита и называют логическими переменными. Если высказывание истинно,
- 12. Так, например, предложение " Трава зеленая" следует считать высказыванием, так как оно истинное. Записывается: А=1 Предложение
- 13. Пусть через А обозначено высказывание "Тимур поедет летом на море", а через В — высказывание "Тимур
- 14. Тогда составное высказывание "Тимур летом побывает и на море, и в горах" можно кратко записать как
- 15. A – Сейчас идет дождь. B – Форточка открыта. A и B A или не B
- 16. Операции над логическими высказываниями
- 17. Операция НЕ Операция, выражаемая словом "не", называется инверсией или отрицанием и обозначается чертой над высказыванием. Если
- 18. Высказывание А истинно, когда A ложно, и ложно, когда A истинно. Пример. "Луна — спутник Земли"
- 19. 1 0 0 1 таблица истинности операции НЕ Таблица истинности логического выражения F – это таблица,
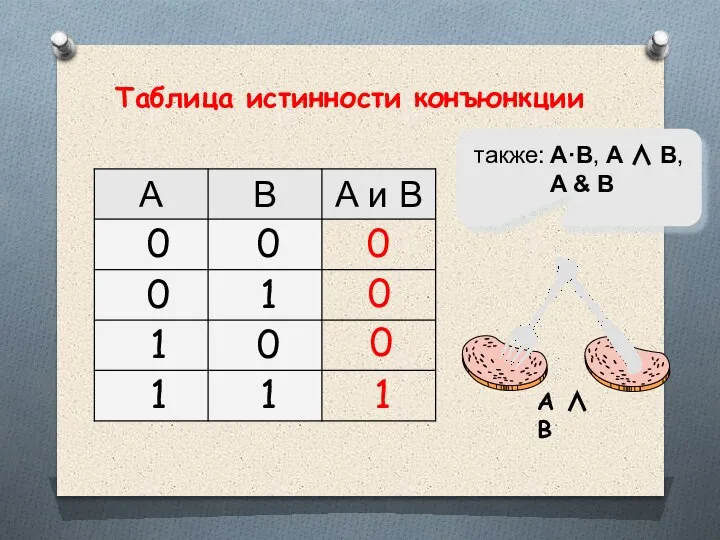
- 20. Операция И Операция, выражаемая связкой "и", называется конъюнкцией (лат. conjunctio — соединение) или логическим умножением и
- 21. Высказывание А · В истинно тогда и только тогда, когда оба высказывания А и В истинны.
- 22. 1 0 также: A·B, A ∧ B, A & B 0 0 A ∧ B Таблица
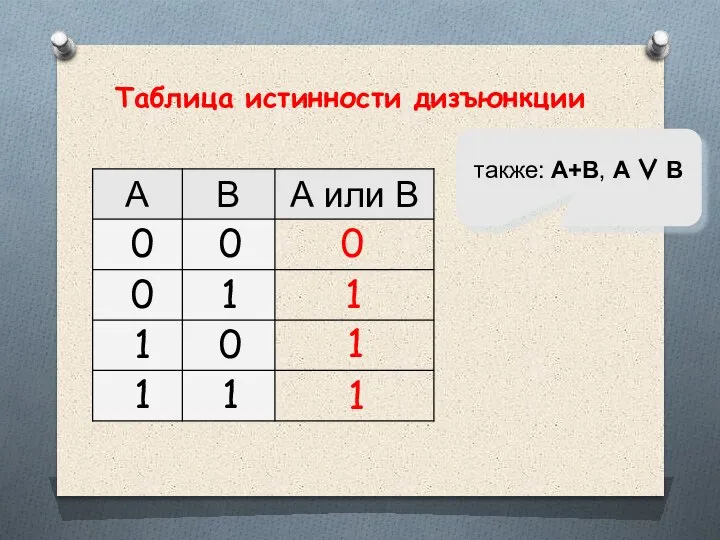
- 23. Операция ИЛИ Операция, выражаемая связкой "или" называется дизъюнкцией (лат. disjunctio — разделение) или логическим сложением и
- 24. Высказывание А v В ложно тогда и только тогда, когда оба высказывания А и В ложны.
- 25. 1 0 также: A+B, A ∨ B 1 1 Таблица истинности дизъюнкции
- 26. Базовый набор операций С помощью операций И, ИЛИ и НЕ можно реализовать любую логическую операцию.
- 27. Операция ЕСЛИ-ТО Операция, выражаемая связками "если ..., то", "из ... следует", "... влечет ...", называется импликацией
- 28. A – "Работник хорошо работает". B – "У работника хорошая зарплата". 1 1 1 0 Таблица
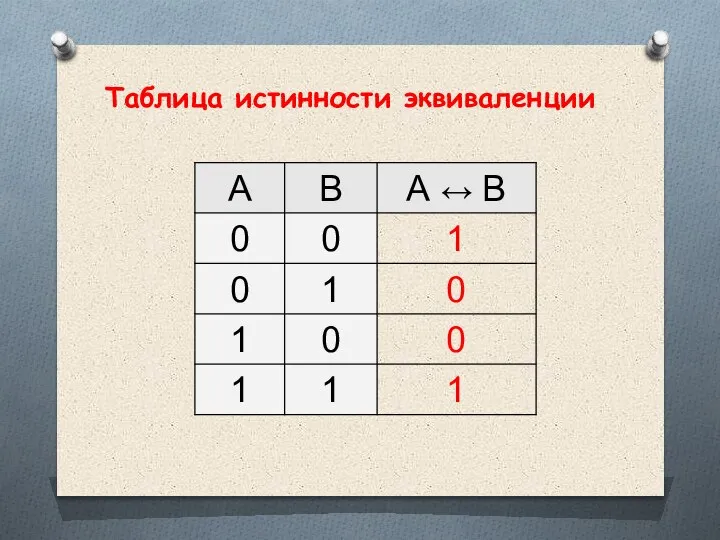
- 29. Операция РАВНОСИЛЬНО Операция, выражаемая связками "тогда и только тогда", "необходимо и достаточно", "... равносильно ...", называется
- 30. Таблица истинности эквиваленции
- 31. С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической
- 32. Определение логической формулы: 1. Всякая логическая переменная и символы "истина" ("1") и "ложь" ("0") - формулы.
- 33. Порядок выполнения логических операций в сложном логическом выражении 1.Инверсия; 2. Конъюнкция; 3. Дизъюнкция; 4. Импликация; 5.
- 34. Определите истинность составного высказывания: (А&В) & (C\/D), состоящего из простых высказываний: А = {Принтер – устройство
- 35. Даны простые высказывания: А = {Принтер – устройство ввода информации}, В = {Процессор – устройство обработки
- 36. Логические выражения и их таблицы истинности Составные высказывания в алгебре логики записываются с помощью логических выражений.
- 37. Таблица истинности - это табличное представление логической схемы (операции), в котором перечислены все возможные сочетания значений
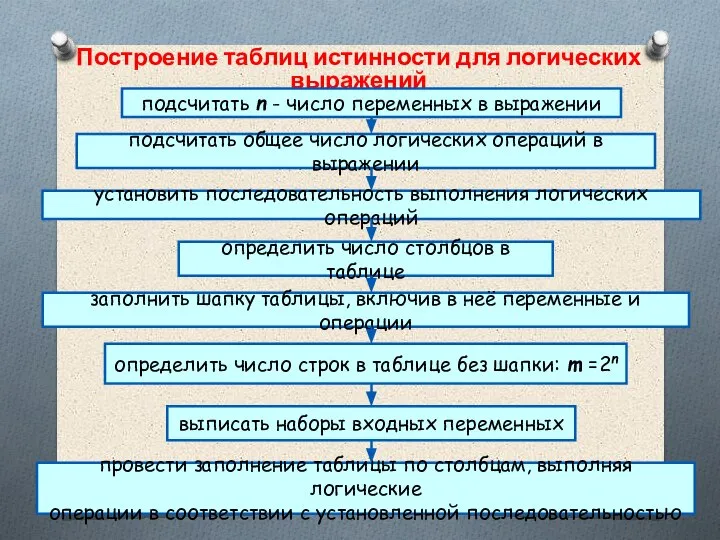
- 38. Построение таблиц истинности для логических выражений подсчитать n - число переменных в выражении подсчитать общее число
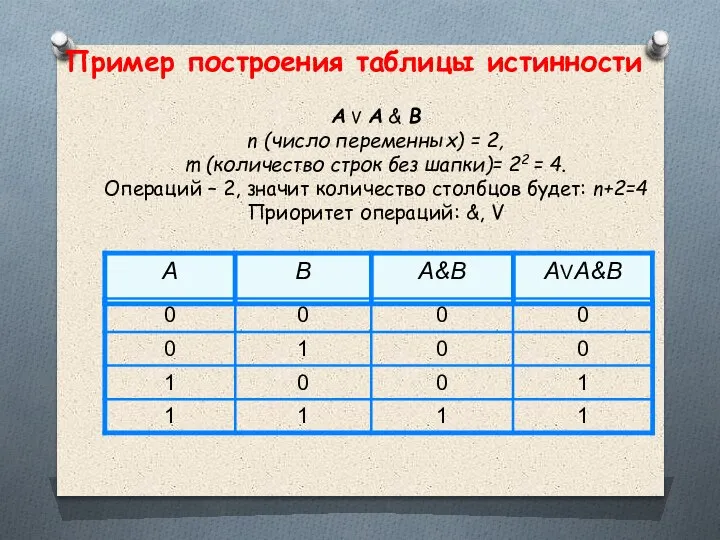
- 39. А V A & B n (число переменных) = 2, m (количество строк без шапки)= 22
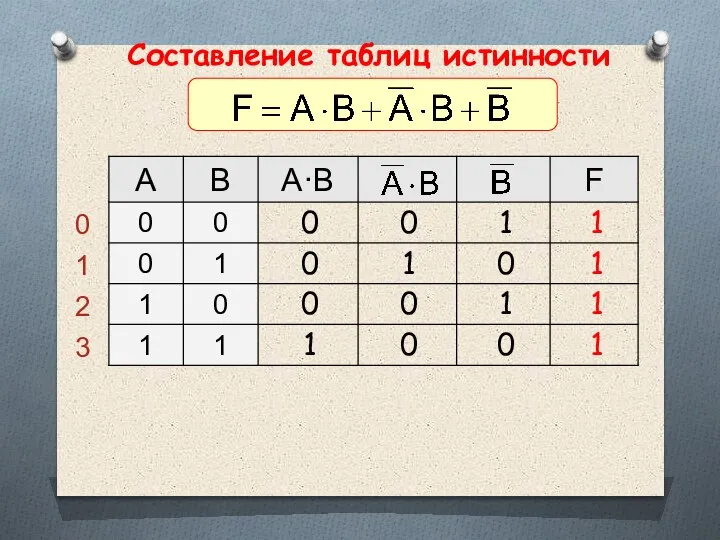
- 40. Составление таблиц истинности
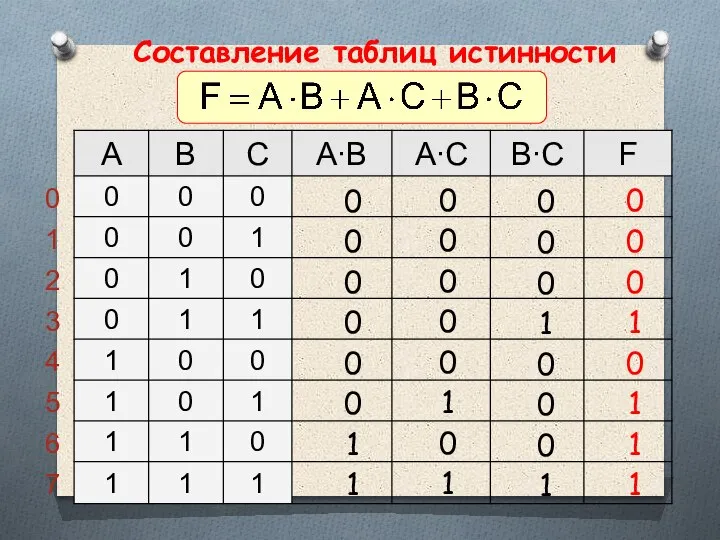
- 41. Составление таблиц истинности
- 42. ЗАКОНЫ АЛГЕБРЫ ЛОГИКИ
- 43. Закон тождества A = A Закон тождества означает, что в процессе рассуждения нельзя подменять одну мысль
- 44. Закон непротиворечия A & notA = 0 Не могут быть одновременно истинны утверждение и его отрицание.
- 45. Закон исключения третьего A and not A = 1 В один и тот же момент времени
- 46. Закон двойного отрицания Not (notA)=1 Если отрицать дважды некоторое высказывание, то в результате получается исходное высказывание.
- 47. ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ КОМПЬЮТЕРА
- 48. Логический элемент компьютера — это часть электронной логической схемы, которая реализует элементарную логическую функцию.
- 49. Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ, И—НЕ, ИЛИ—НЕ и другие.
- 50. Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию, но не указывает на
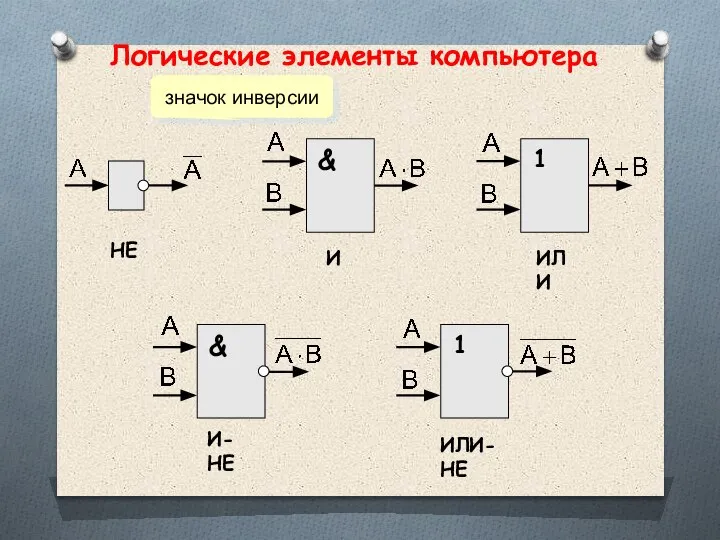
- 51. Логические элементы компьютера НЕ И ИЛИ ИЛИ-НЕ И-НЕ значок инверсии
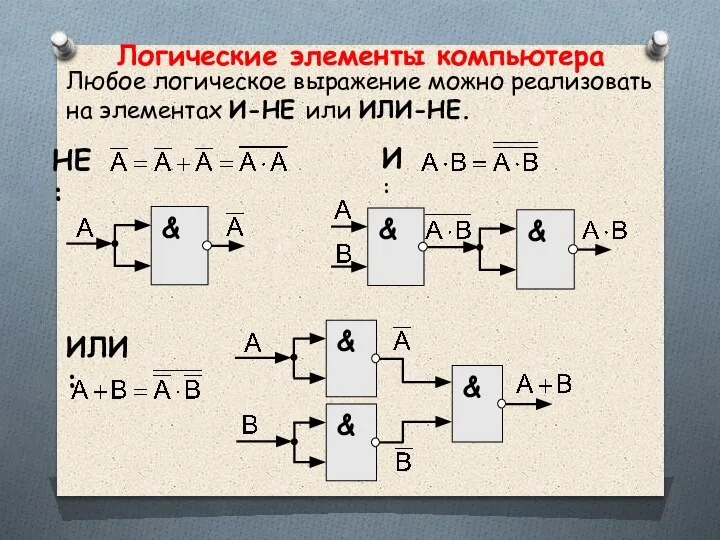
- 52. Логические элементы компьютера Любое логическое выражение можно реализовать на элементах И-НЕ или ИЛИ-НЕ. И: НЕ: ИЛИ:
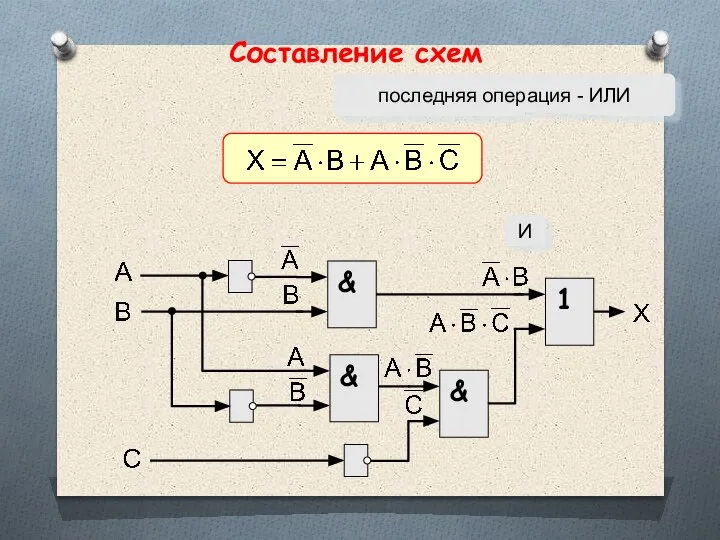
- 53. Составление схем последняя операция - ИЛИ & И
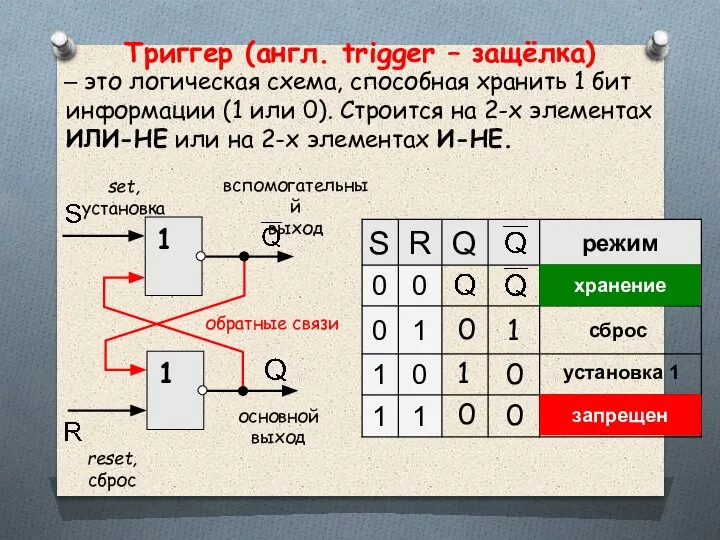
- 54. Триггер (англ. trigger – защёлка) – это логическая схема, способная хранить 1 бит информации (1 или
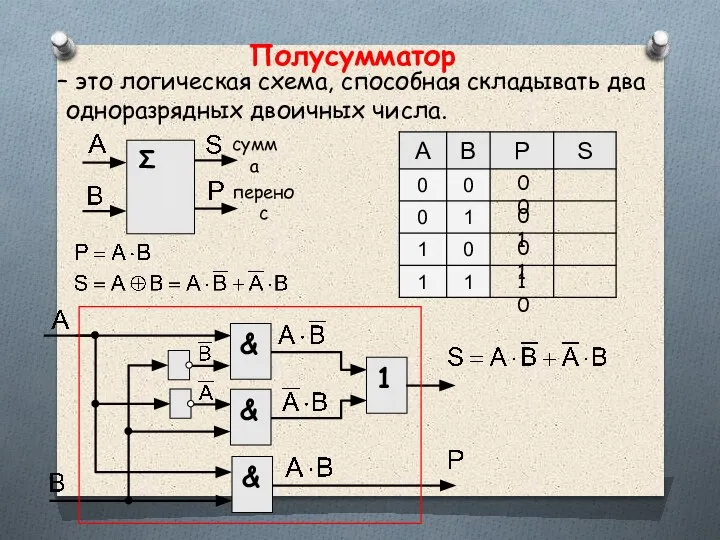
- 55. Полусумматор – это логическая схема, способная складывать два одноразрядных двоичных числа. 0 0 0 1 0
- 57. Скачать презентацию









































 2) Типы алгоритмов_ОК_ГОТ
2) Типы алгоритмов_ОК_ГОТ Введение в ANSYS
Введение в ANSYS Геоинформационные технологии в системах территориального управления
Геоинформационные технологии в системах территориального управления Урок 8 Создание графических изображений
Урок 8 Создание графических изображений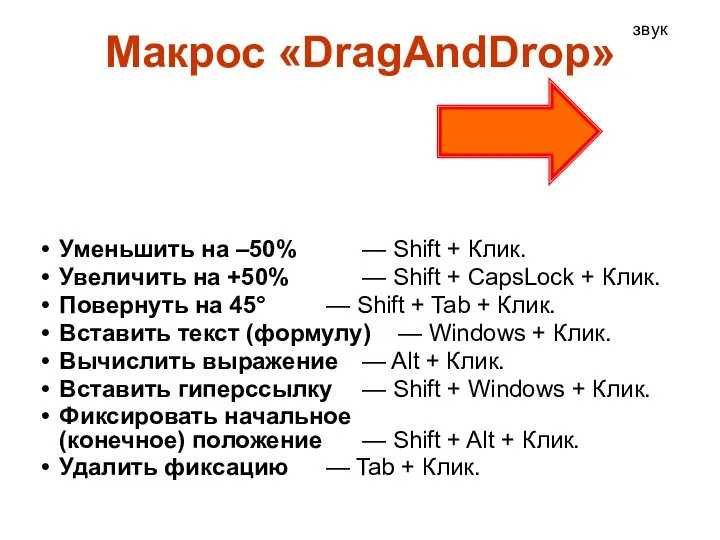 Макрос DragAndDrop
Макрос DragAndDrop Road to success. Макет сайта
Road to success. Макет сайта Электронные библиотечные системы
Электронные библиотечные системы Что такое массив?
Что такое массив? CRM система для УрФУ
CRM система для УрФУ НЕ стандартные диаграммы Node Tree Дерево узлов
НЕ стандартные диаграммы Node Tree Дерево узлов Информационная безопасность
Информационная безопасность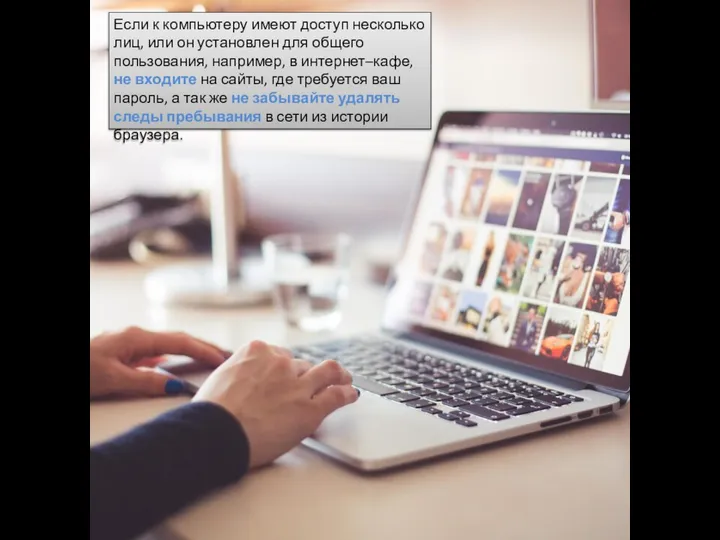 Безопасность в интернете
Безопасность в интернете Конструктивные решения блоков питания и источников бесперебойного питания. Технология подключения и настройки
Конструктивные решения блоков питания и источников бесперебойного питания. Технология подключения и настройки Компьютерные вирусы
Компьютерные вирусы Пример графики
Пример графики Ведущий и его роль в игре
Ведущий и его роль в игре 841f5b390ae2e214
841f5b390ae2e214 Презентация на тему Основы HTML
Презентация на тему Основы HTML  Информационная инфраструктура
Информационная инфраструктура Application presentation template
Application presentation template Изучение библиографических стилей. Составление списка источников. Лабораторная работа 7
Изучение библиографических стилей. Составление списка источников. Лабораторная работа 7 CSS — формальный язык описания внешнего вида документа, написанного с использованием языка разметки
CSS — формальный язык описания внешнего вида документа, написанного с использованием языка разметки Международный день защиты информации
Международный день защиты информации Сравнительный анализ дизайна интернет-сайтов
Сравнительный анализ дизайна интернет-сайтов Типы информационных моделей. 8 класс
Типы информационных моделей. 8 класс Insignia. Исследование
Insignia. Исследование Interfaces Polymorphism
Interfaces Polymorphism Changes and new features
Changes and new features