Измерение связи между явлениями или признаками. Корреляция

Известно, что все явления в природе и обществе находятся во взаимной связи. При изучении связи между явлениями:
Во-первых, следует провести качественный анализ, позволяющий установить возможность связи между явлениями, определить ее характер, выяснить имеется ли между ними причинно-следственная связь, или оба из изучаемых явлений зависят от третьего.
Во-вторых, целесообразно статистически проверить наличие связи.
Для этих целей служит коэффициент корреляции, который одним числом дает оценку степени связи между изучаемыми явлениями, определяет ее силу и направление, позволяет распутать цепь причин и привлечь к их объяснению ряд различных факторов.

ОСНОВНЫЕ ВОПРОСЫ И КЛЮЧЕВЫЕ ПОНЯТИЯ
Различные явления или признаки могут иметь между собой две формы связи: функциональную и корреляционную.
Функциональная связь характерна для явлений, между которыми существует строгая зависимость, то есть изменение на определенную величину одного явления (признака) сопровождается строго определенным изменение другого явления (признака). При этом зависимость проявляется настолько сильно, что каждому определенному значению влияющего признака (х) всегда соответствует строго определенное, единственное значение результативного признака (у). Такая связь встречается только в идеальных условиях, когда предполагается, что никаких посторонних влияний нет.
Функциональная связь в основном имеет место там, где ее можно представить в виде уравнения, формулы (например, радиусу круга соответствует определенная площадь круга, степень расширения тела определяется температурой нагревания и т.п.).

В биологии и медицине, как правило, встречается корреляционная связь. Корреляционная связь – это связь, при которой от изменения одного явления зависит главным образом, но не исключительно, изменение другого явления, значения которого варьируют в определенных размерах вокруг своей средней величины. Например, известно, что масса тела человека зависит от изменения его роста.
Эти колебания массы тела варьируют в определенных размерах вокруг своей средней величины, т.к. связаны еще с питанием, физической нагрузкой, обменом веществ, состоянием здоровья и т.п.
Другими примерами могут служить, связь уменьшения уровня инфекционной заболеваемости с увеличением процента привитых лиц, взаимосвязь между цветом волос и цветом глаз (темные или светлые), зависимость заболеваемости раком кожи от степени пигментации кожных покровов, связь между уровнем вредных производных факторов и частотой профессиональных заболеваний.
По своему характеру корреляционная связь подразделяется на следующие виды:
- причинно-следственную;
- обусловленную;
- параллельную.

Причинно-следственная связь проявляется в тех случаях, когда изменение одного явления (признака) является причиной изменения другого явления (признака). Например, увеличение числа диспансерных больных, получивших противорецидивное лечение, приводит к снижению частоты обострения хронических заболеваний, внедрение новых технологий на производстве приводит к изменению показателей производственного травматизма.
Обусловленная связь присутствует в тех случаях, когда изменение одного явления (признака) как бы создаст условия, способствующие изменению другого явления или признака. Например, высокая температура воздуха в летнее время может привести к росту частоты сердечно-сосудистых заболеваний, увеличению уровня пищевых отравлений среди населения, а понижение температуры воздуха в зимнее время сопровождается увеличением уровня заболеваемости населения простудными болезнями. Но при наличии ряда обстоятельств (например, проведение профилактических мероприятий) этого может не произойти.

Для параллельной связи характерно параллельное изменение двух явлений или признаков в зависимости от третьего. Например, изменение роста ребенка сопровождается изменением массы его тела и окружности груди. Но параметры таких изменений неодинаковы.
Различают прямолинейную и криволинейную корреляционную связь.
Так, если при относительно равномерном изменении средних значений одного признака проходят равные изменения другого (например, соответствия между изменениями уровней максимального и минимального артериального давления) наблюдается прямолинейная корреляционная связь.
При криволинейной зависимости равномерное изменение одного признака сопровождается неравномерными, непропорциональными возрастающими и убывающими изменениями другого признака.

Способами изображения связи могут быть:
таблицы,
рисунки (графики)
коэффициенты корреляции.
Методы корреляции можно применять только при измерении связи между различными признаками только лишь в качественно однородной совокупности. Нельзя, например, сопоставлять рост и массу тела лиц разного пола и возраста.
Изучаемые явления (признаки) могут быть выражены количественно или описательно, представлены сгруппированными или несгруппированными данными.

Выразить количественно – это значит выразить числом (например, рост – в сантиметрах или метрах, массу тела – в килограммах, содержание железа в крови – в мг%, частоту заболеваний в промиллях или продецимиллях), а выразить описательно – значит выразить словесно.
Описательные признаки – обычно альтернативные признаки. Альтернативным называют случай, когда вариация исчерпывается двумя возможностями: заболел или не заболел, привит или не привит, выздоровел или не выздоровел.
Сгруппированные данные – это данные, объединенные в группы по их величине в пределах одного интервала. В виде сгруппированных данных могут быть представлены значения одного из изучаемых явлений (признаков) или значения обоих признаков: влияющего (х) и результативного (у). Чаще всего группируют данные при большом числе наблюдений.
Несгруппированные данные – это данные каждого из изучаемых признаков, выраженные одним числом.

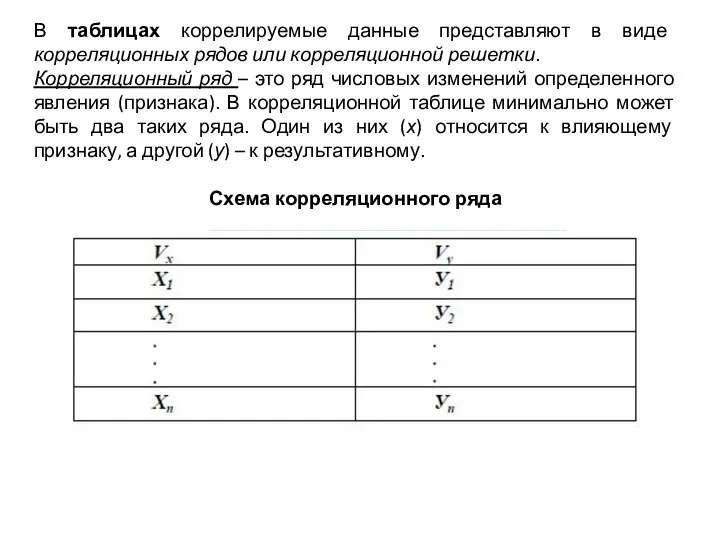
В таблицах коррелируемые данные представляют в виде корреляционных рядов или корреляционной решетки.
Корреляционный ряд – это ряд числовых изменений определенного явления (признака). В корреляционной таблице минимально может быть два таких ряда. Один из них (х) относится к влияющему признаку, а другой (у) – к результативному.
Схема корреляционного ряда

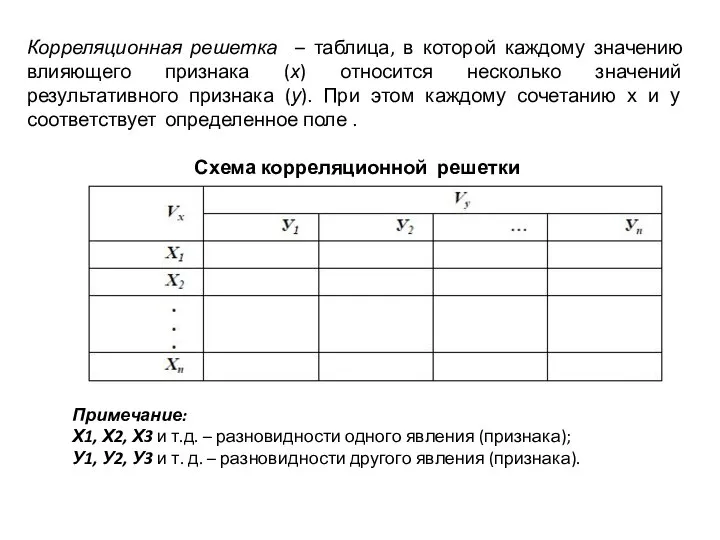
Корреляционная решетка – таблица, в которой каждому значению влияющего признака (х) относится несколько значений результативного признака (у). При этом каждому сочетанию х и у соответствует определенное поле .
Схема корреляционной решетки
Примечание:
Х1, Х2, Х3 и т.д. – разновидности одного явления (признака);
У1, У2, У3 и т. д. – разновидности другого явления (признака).

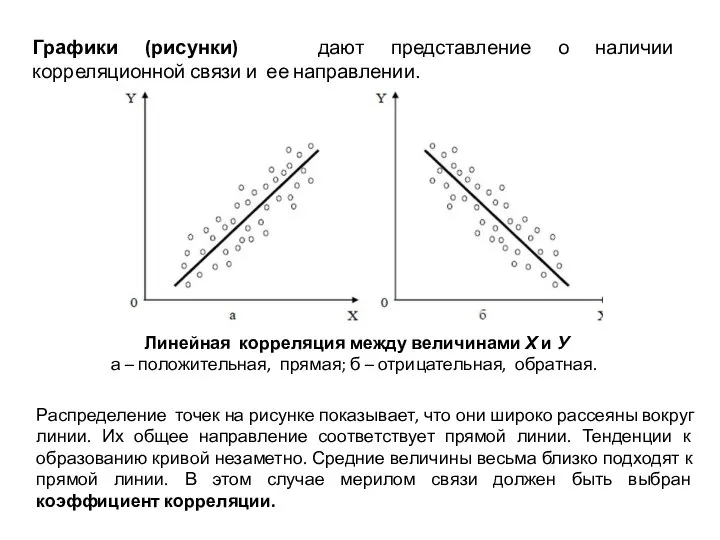
Графики (рисунки) дают представление о наличии корреляционной связи и ее направлении.
Линейная корреляция между величинами Х и У
а – положительная, прямая; б – отрицательная, обратная.
Распределение точек на рисунке показывает, что они широко рассеяны вокруг линии. Их общее направление соответствует прямой линии. Тенденции к образованию кривой незаметно. Средние величины весьма близко подходят к прямой линии. В этом случае мерилом связи должен быть выбран коэффициент корреляции.

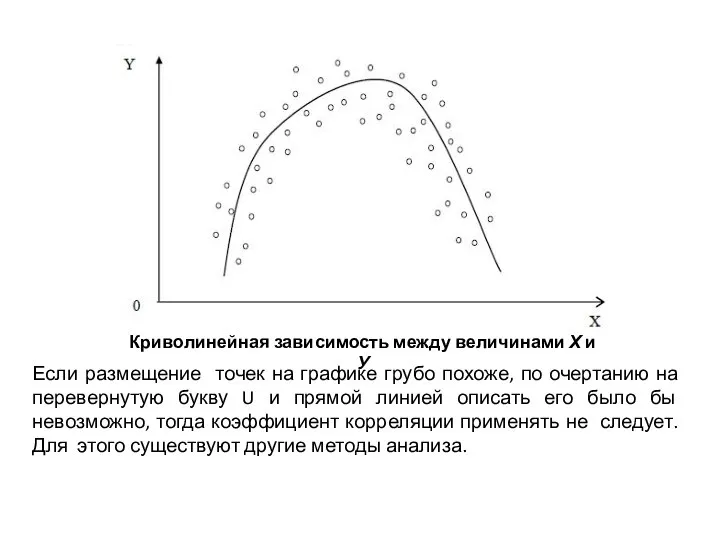
Криволинейная зависимость между величинами Х и У
Если размещение точек на графике грубо похоже, по очертанию на перевернутую букву U и прямой линией описать его было бы невозможно, тогда коэффициент корреляции применять не следует. Для этого существуют другие методы анализа.

Таблицы и графики дают лишь представление о наличии и направлении связи. Однако измерить и оценить статистическую достоверность этой связи можно при помощи коэффициента корреляции.
Существует много способов вычисления таких коэффициентов. Выбор одного какого-либо из них находится в зависимости от следующих факторов:
1. Каким образом выражены признаки изучаемых явлений, находящихся во взаимной связи, – описательно или количественно.
2. В каком виде представлены данные – сгруппированном или несгруппированном.
3. Требуется ли измерить связь между двумя явлениями или между несколькими.
Наиболее простыми для расчета и широко используемыми являются:
коэффициент линейной корреляции (rху);
коэффициент ранговой корреляции (р);
коэффициент ассоциации (Q).

По направлению связь может быть прямой и обратной.
Прямой (положительной) связью называется такая связь, когда оба явления изменяются в одном направлении. Например, с ухудшением питания ухудшаются показатели здоровья населения. Обозначается знаком плюс (+)
Обратной (отрицательной) связью называется связь, когда одно явление увеличивается, а другое при этом уменьшается. Обозначается знаком минус (–).

По силе связи коэффициенты корреляции колеблются от единицы (полная функциональная связь) до нуля (отсутствие связи). Промежуточные значения (1>r>0) говорят о наличие связи более или менее сильной степени. Чем больше среднему значению одного признака соответствует значений другого признака, тем выше сила связи между ними. Оценка размеров корреляции может производиться по следующей схеме.
Схема оценки коэффициента корреляции

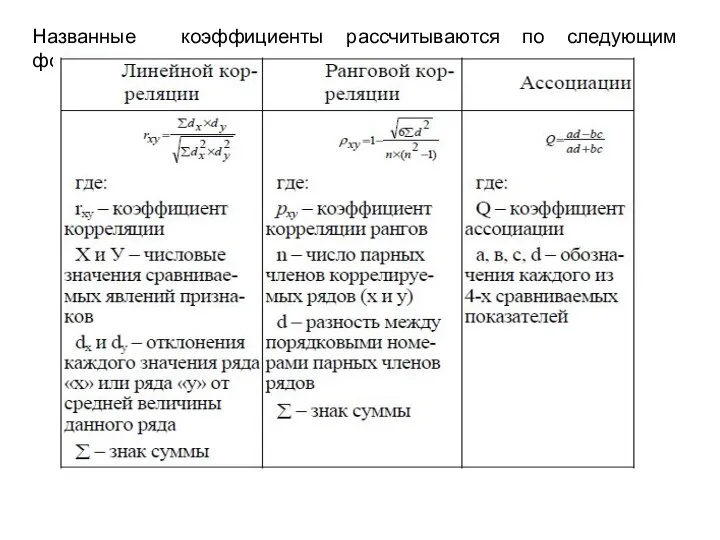
1. КОЭФФИЦИЕНТ ЛИНЕЙНОЙ КОРРЕЛЯЦИИ
Наиболее точный. Его используют:
при прямолинейной зависимости между изучаемыми явлениями (признаками);
небольшом числе наблюдении (число парных вариант не более 30);
несгруппированных данных.
Коэффициент корреляции (rху) одним числом измеряет силу связи между изучаемыми явлениями и дает представление о ее направлении;

2. КОЭФФИЦИЕНТ РАНГОВОЙ КОРРЕЛЯЦИИ
Применяют в том случае, когда не нужна большая точность оценки силы связи.
Его используют:
при прямолинейной, криволинейной зависимости между изучаемыми явлениями или когда определить ее вид невозможно;
небольшом числе наблюдений (не больше 30);
при сравнении не только количественных, но и качественных (атрибутивных) признаков;
при измерении связи между альтернативными признаками, имеющими несколько градаций;
когда в сравниваемых рядах величин имеются открытые группы, не имеющие четких границ (например, в ряду величин, характеризующих стаж работы, могут быть группы: «до 5 лет», «более 20 лет»).

3. КОЭФФИЦИЕНТ АССОЦИАЦИИ
Является наиболее точным и находит применение для измерения связи между альтернативными признаками.

Названные коэффициенты рассчитываются по следующим формулам:

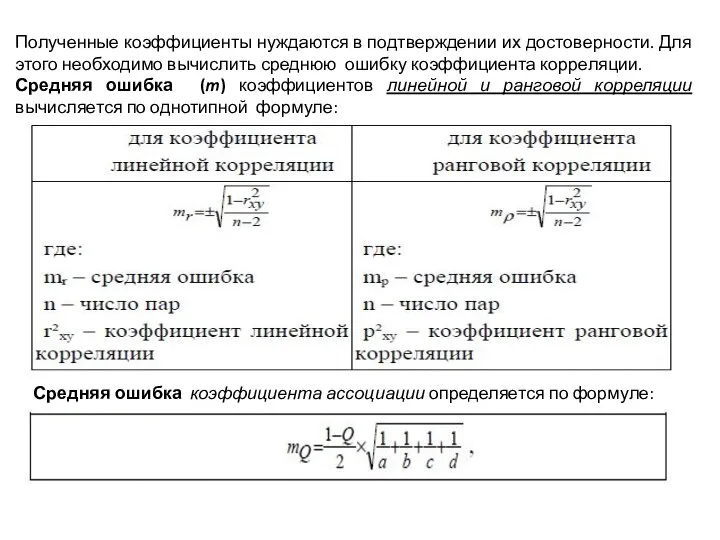
Полученные коэффициенты нуждаются в подтверждении их достоверности. Для этого необходимо вычислить среднюю ошибку коэффициента корреляции.
Средняя ошибка (m) коэффициентов линейной и ранговой корреляции вычисляется по однотипной формуле:
Средняя ошибка коэффициента ассоциации определяется по формуле:

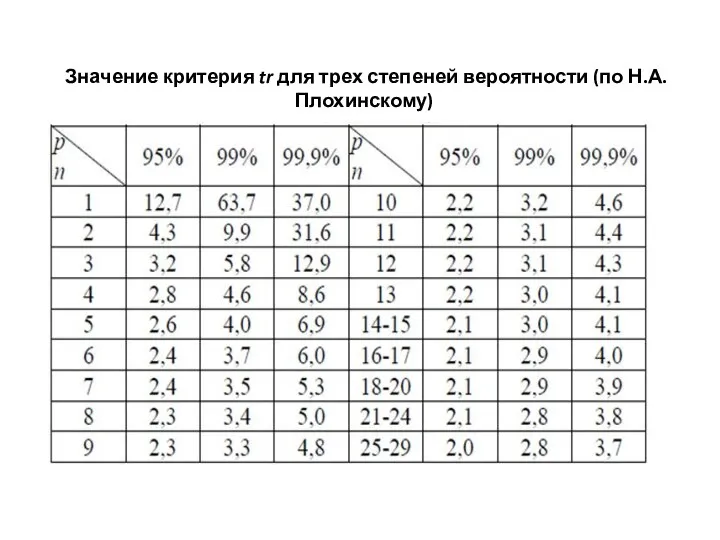
Достоверность коэффициентов корреляционной связи определяется с помощью критерия достоверности – t, который вычисляется путем деления величины показателя на величину рассчитанной для него средней ошибки:
Коэффициенты корреляционной связи считаются достоверными, если они в 3 (три) раза превышают свою среднюю ошибку;
При малом числе наблюдений значение критерия достоверности, рассчитанное для конкретного коэффициента, сравнивается с критериями в специальной таблице (по Н.А. Плохинскому , соответствующими числу наблюдений в данном исследовании.

Значение критерия tr для трех степеней вероятности (по Н.А. Плохинскому)

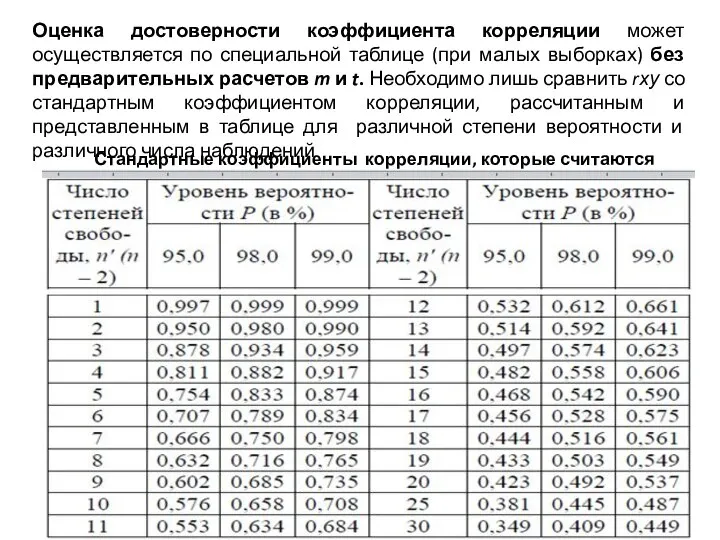
Оценка достоверности коэффициента корреляции может осуществляется по специальной таблице (при малых выборках) без предварительных расчетов m и t. Необходимо лишь сравнить rху со стандартным коэффициентом корреляции, рассчитанным и представленным в таблице для различной степени вероятности и различного числа наблюдений
Стандартные коэффициенты корреляции, которые считаются достоверными (по Л.С. Каменскому)

МЕТОДИКА ВЫЧИСЛЕНИЯ КОЭФФИЦИЕНТА ЛИНЕЙНОЙ КОРРЕЛЯЦИИ
1-й способ
Алгоритмы расчета коэффициента линейной корреляции (rху), его ошибки (mr) и коэффициента достоверности (tr)

1. Записать исходные данные в виде двух вариационных рядов (графы 1 и 2)
2. Найти суммы вариант в каждом вариационном ряду (Σх и Σу) и определить средние арифметические величины (Мх и Му) – графы 1 и 2.
3. Найти dx и dу – отклонения каждой варианты от средних величин (графы 3 и 4).
4. Полученные отклонения перемножить попарно (dх × dу) и найти сумму полученных произведений (Σdх × dу) – графа 5.
5. Каждое отклонение в обоих рядах возвести в квадрат и определить сумму квадратов отклонений ряда Vх (графа 6) и ряда Vу (графа 7).
6. Определить произведение Σd²х × Σd²у и из произведения извлечь квадратный корень Σd²х × Σd²у
7. Подставить полученные данные в формулу и рассчитать коэффициент корреляции (Rху) – графа 8.
8. Подставить необходимые данные в формулу и рассчитать среднюю ошибку (mr) коэффициента корреляции – графа 8.
9. Подставить необходимые данные в формулу и рассчитать коэффициент достоверности (tr) – графа 8.

2-й способ
При наличии вычислительной техники расчет коэффициента линейной корреляции производится по следующей схеме
Алгоритм расчета (на ЭВМ) коэффициента корреляции (Rху)

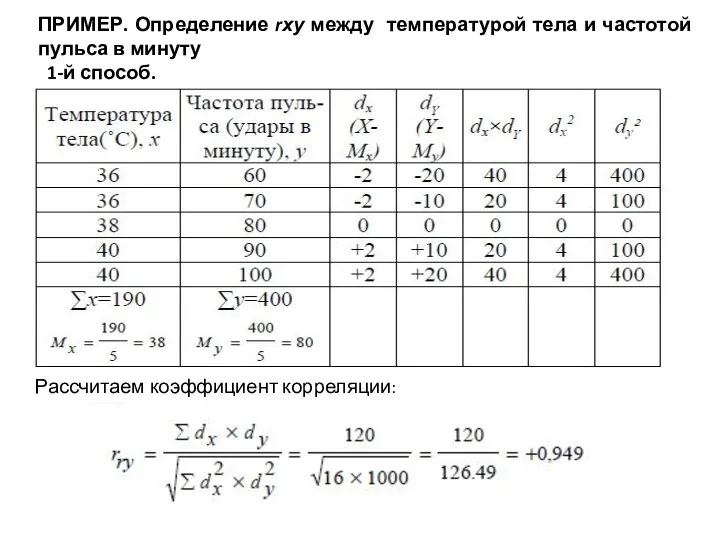
ПРИМЕР. Определение rху между температурой тела и частотой пульса в минуту
1-й способ.
Рассчитаем коэффициент корреляции:

Рассчитаем среднюю ошибку (mr) коэффициента достоверности:
Рассчитаем коэффициент достоверности tr:
Оценим критерий tr по специальным таблицам (по Н.А. Плохинскому) и (по Л.С. Каменскому)
Вывод. Коэффициент корреляции, равный 0,949, достоверен с вероятностью безошибочного прогноза р>95%, так как при n=3 (5 – 2) полученный нами критерий t будет больше tтабл.=3,2 (р=95%) и меньше tтабл.=5,8 (р=99%). Материалы выборочного исследования позволяют утверждать, что в генеральной совокупности существует сильная прямая связь между температурой тела и частотой пульса.

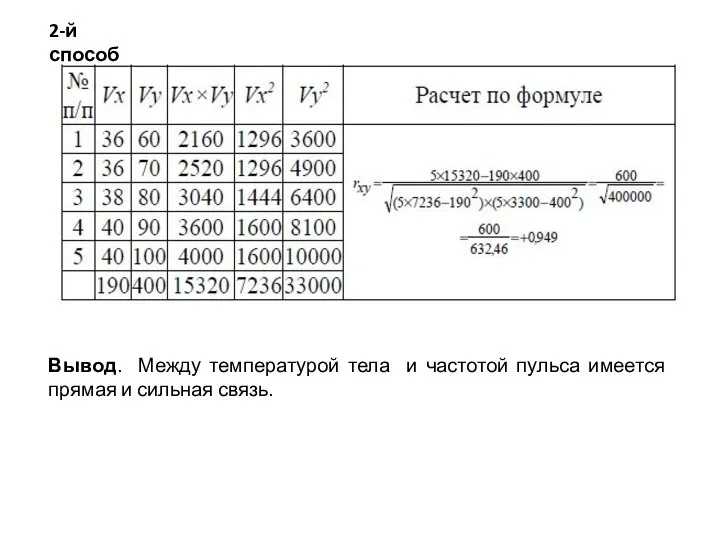
2-й способ
Вывод. Между температурой тела и частотой пульса имеется прямая и сильная связь.

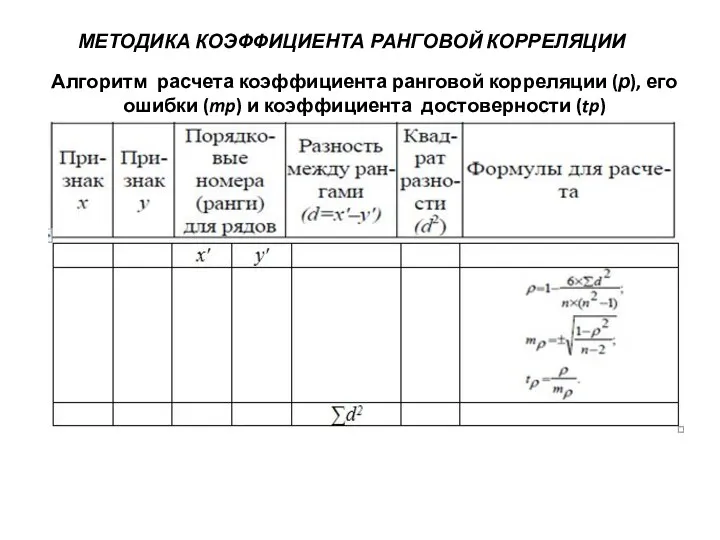
МЕТОДИКА КОЭФФИЦИЕНТА РАНГОВОЙ КОРРЕЛЯЦИИ
Алгоритм расчета коэффициента ранговой корреляции (р), его ошибки (mp) и коэффициента достоверности (tp)

1. Составить ряды из парных признаков (графы 1 и 2).
2. Каждую величину признака заменить ранговым (порядковым) номером – х′ и у′. (в тех случаях, когда имеется несколько одинаковых по величине чисел, порядковый номер обозначают средним числом из суммы очередных порядковых их номеров). Ранжировать значения обоих рядов в строго определенном направлении от меньшей величины к большей или от большей к меньшей (графы 3 и 4).
3. Определить разность между рангами для каждой пары членов ряда (по каждой строке) – графа 5.
4. Возвести в квадрат каждое из полученных значений разности между рангами и определить сумму квадратов разности рангов (Σd²) – графа 6.
5. Подставить полученные данные в формулу и рассчитать коэффициент корреляции рангов – графа 7.
6. Подставить необходимые данные в формулу и рассчитать среднюю ошибку (mp) коэффициента ранговой корреляции – графа 7.
7. Подставить необходимые данные в формулу и рассчитать коэффициент достоверности (tp) – графа 7.

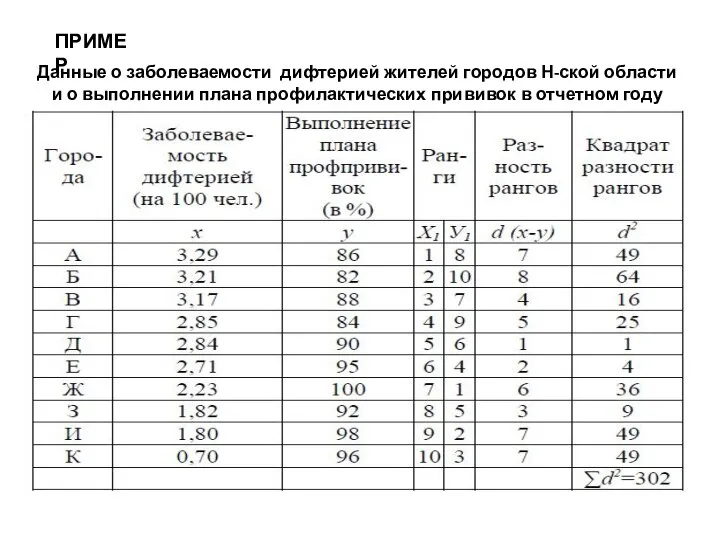
ПРИМЕР
Данные о заболеваемости дифтерией жителей городов Н-ской области и о выполнении плана профилактических прививок в отчетном году

Рассчитываем коэффициент ранговой корреляции:
Рассчитаем среднюю ошибку (mp):
Рассчитаем коэффициент достоверности:

Условие достоверности коэффициента корреляции рангов
Таким образом, –0,83>3×0,197 или –0,83>0,591 т.е. полученные результаты достоверны.
Вывод. Полученный коэффициент корреляции рангов статистически достоверен. Следовательно, можно говорить о сильной, обратной связи между заболеваемостью дифтерией и процентом выполнения плана профилактических прививок.
Заболеваемость выше в тех городах, где план профилактических прививок выполнен недостаточно.

МЕТОДИКА ВЫЧИСЛЕНИЯ КОЭФФИЦИЕНТА АССОЦИАЦИИ
Алгоритм расчета коэффициента ассоциации (Q), его ошибки (ma) и коэффициента достоверности (ta).
1.Построить четырехпольную таблицу. В первом столбце этой таблицы наносят обе разновидности одного явления – Х1 и Х2, а в первой строке – обе разновидности второго – У1 и У2.При этом Х1 и У2 обозначают положительные разновидности (например, выздоровевшие, иммунизированные и т. д.), а Х2 и У2 – отрицательные (например, не выздоровевшие, не иммунизированные). Обозначить через буквы а, в, с, d четыре поля, в которые внести исходные данные:

2. Вычислить произведения аd и вс.
3. Подставить полученные данные в формулу: Q = (ad- bc)/(ad + bc) и рассчитать коэффициент ассоциации.
4. Подставить необходимые данные в формулу:
и рассчитать среднюю ошибку коэффициента ассоциации.
5. Подставить необходимые данные в формулу:
и рассчитать коэффициент достоверности.

ПРИМЕР
Необходимо определить, влияет ли вакцинация против гриппа на заболеваемость от этой инфекции. Известно, что на промышленном предприятии с общей численностью в 2000 человек 1200 рабочим были сделаны прививки против гриппа, а 800 рабочих остались не привитыми. Заболело из привитых 240 человек, а из непривитых – 320.
Распределение заболевших и не заболевших среди привитых на промышленном предприятии
Вычислим произведения аd и вс:
a×d=240×480=11520
b×c=960×320=307200