Содержание
- 2. План 1. Бинарные операции. 2. Унарные операции.
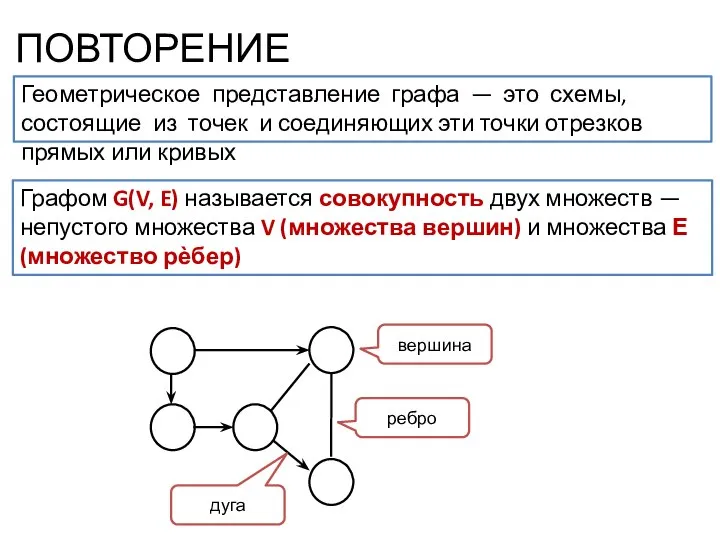
- 3. ПОВТОРЕНИЕ Геометрическое представление графа — это схемы, состоящие из точек и соединяющих эти точки отрезков прямых
- 4. СПОСОБЫ ОПИСАНИЯ ГРАФОВ Способы описания графов Перечисление элементов Изображение Матрица смежности Матрица инциденций Списки смежности
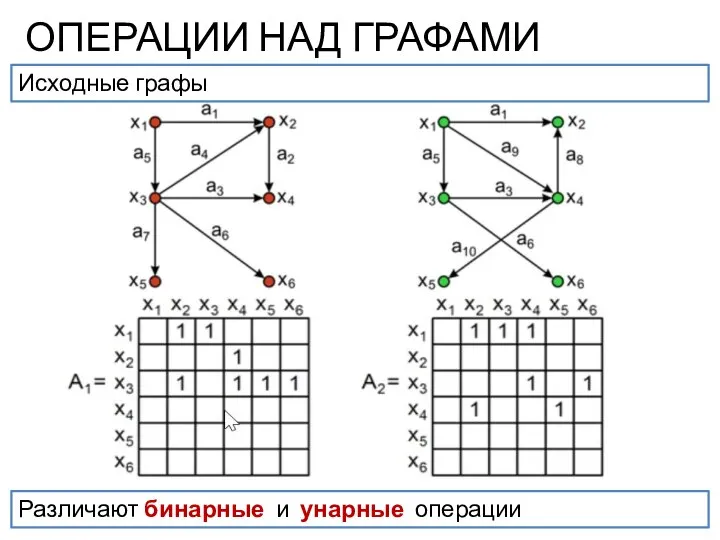
- 5. ОПЕРАЦИИ НАД ГРАФАМИ Исходные графы Различают бинарные и унарные операции
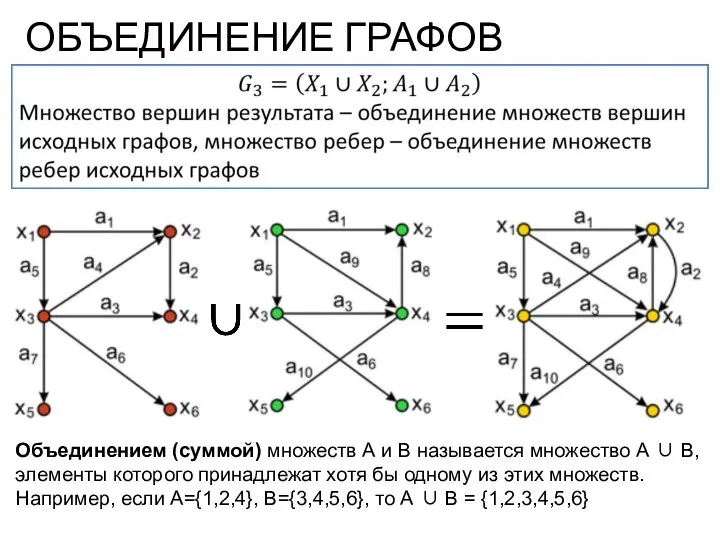
- 6. ОБЪЕДИНЕНИЕ ГРАФОВ Объединением (суммой) множеств А и В называется множество А ∪ В, элементы которого принадлежат
- 7. ОБЪЕДИНЕНИЕ ГРАФОВ При объединении графов матрица смежности результата получается операцией поэлементного логического сложения матриц смежности исходных
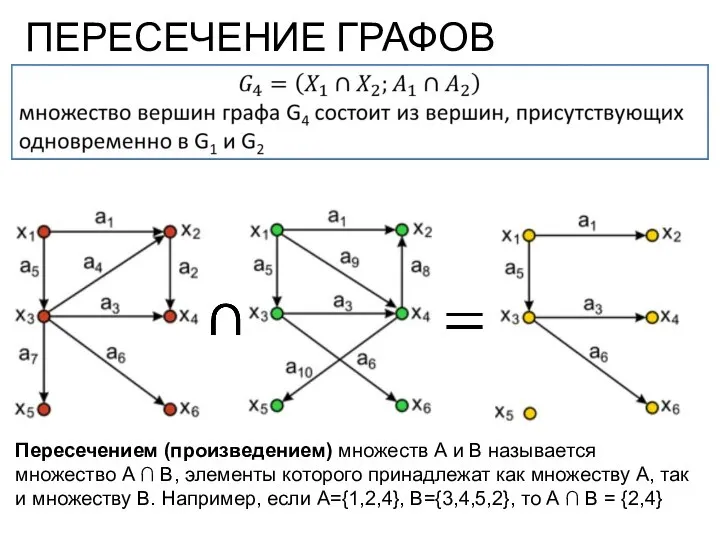
- 8. ПЕРЕСЕЧЕНИЕ ГРАФОВ Пересечением (произведением) множеств А и В называется множество А ∩ В, элементы которого принадлежат
- 9. ПЕРЕСЕЧЕНИЕ ГРАФОВ результирующая матрица смежности получается операцией поэлементного логического умножения матриц смежности исходных графов G1 и
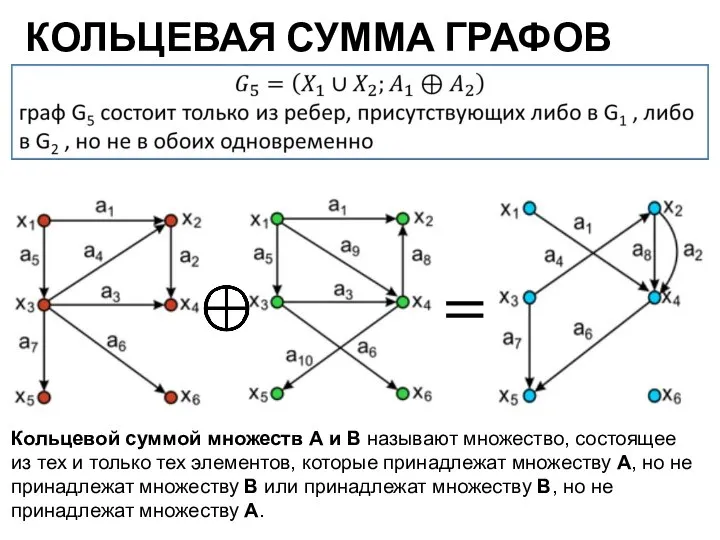
- 10. КОЛЬЦЕВАЯ СУММА ГРАФОВ Кольцевой суммой множеств А и В называют множество, состоящее из тех и только
- 11. КОЛЬЦЕВАЯ СУММА ГРАФОВ результирующая матрица смежности получается операцией поэлементного логического сложения матриц смежности исходных графов
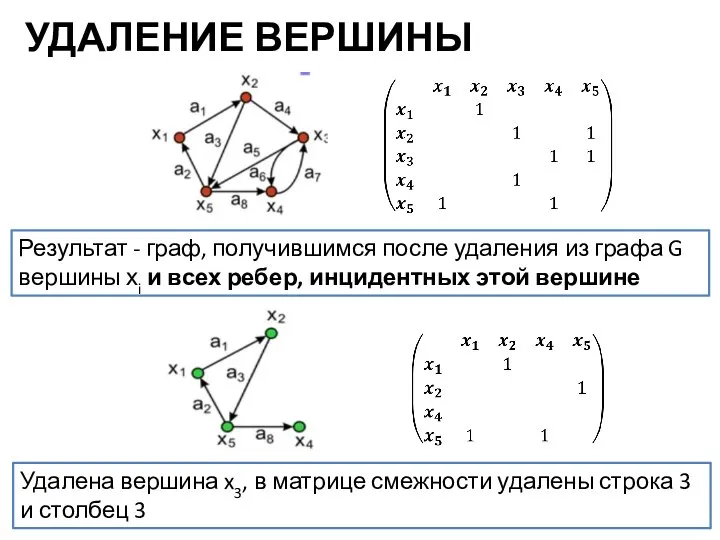
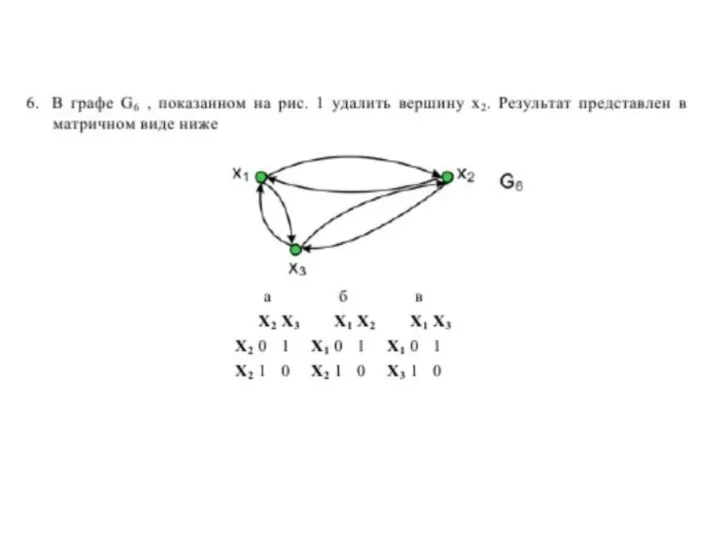
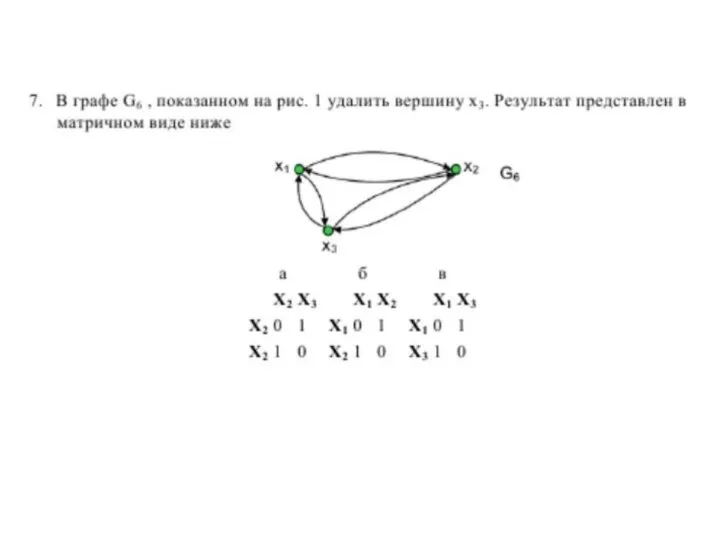
- 12. УДАЛЕНИЕ ВЕРШИНЫ Результат - граф, получившимся после удаления из графа G вершины хi и всех ребер,
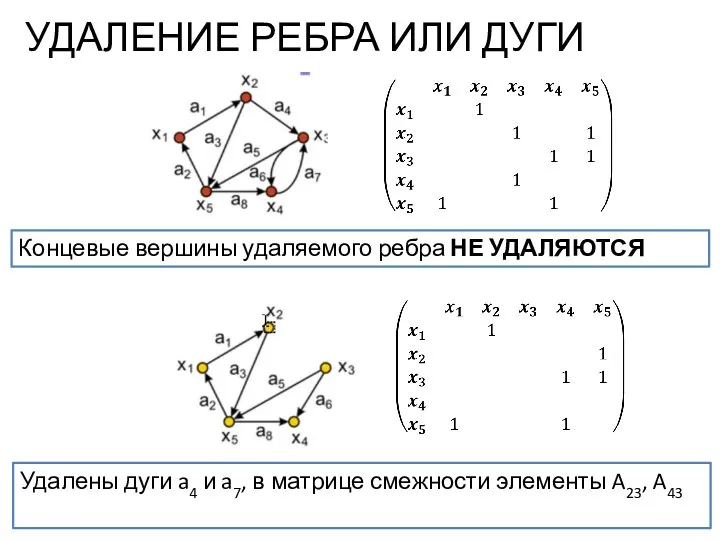
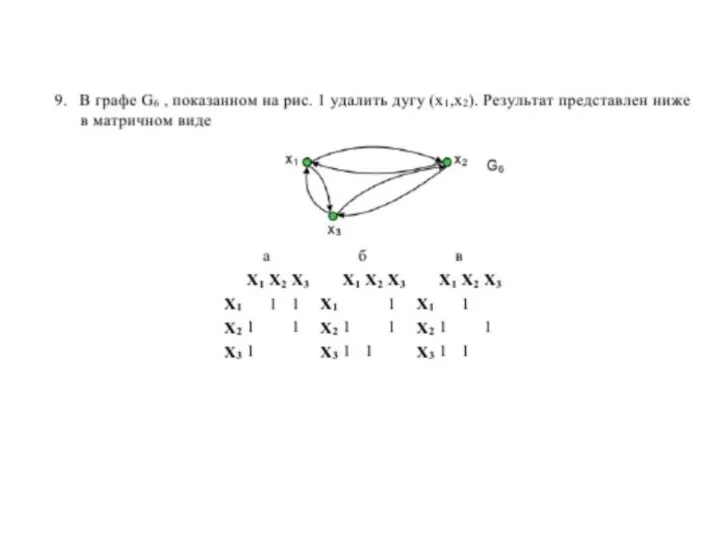
- 13. УДАЛЕНИЕ РЕБРА ИЛИ ДУГИ Концевые вершины удаляемого ребра НЕ УДАЛЯЮТСЯ Удалены дуги a4 и a7, в
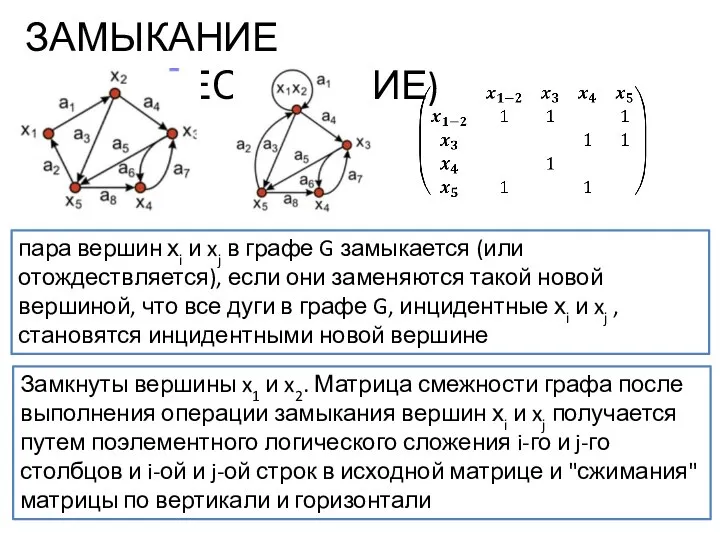
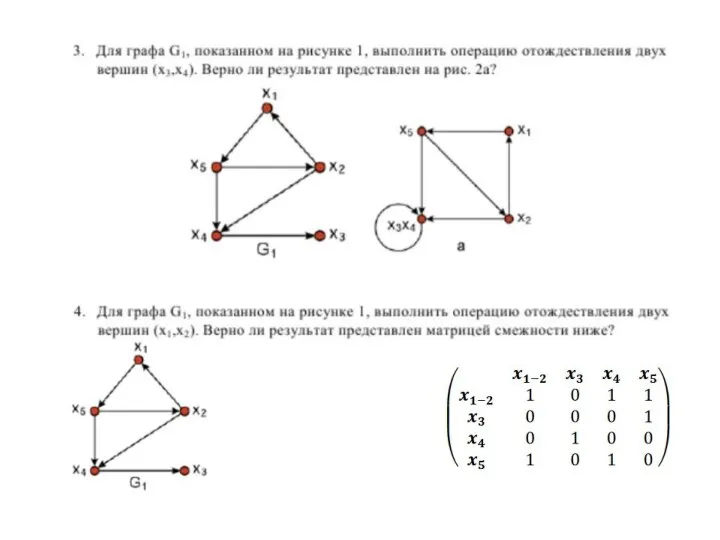
- 14. ЗАМЫКАНИЕ (ОТОЖДЕСТВЛЕНИЕ) пара вершин хi и xj в графе G замыкается (или отождествляется), если они заменяются
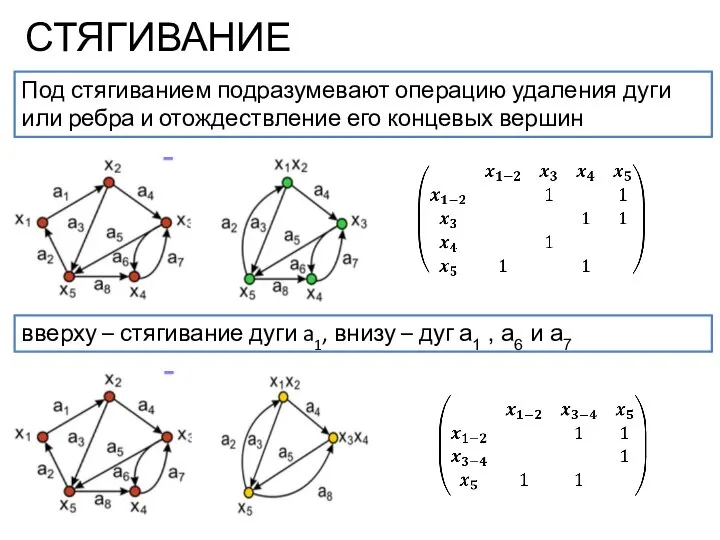
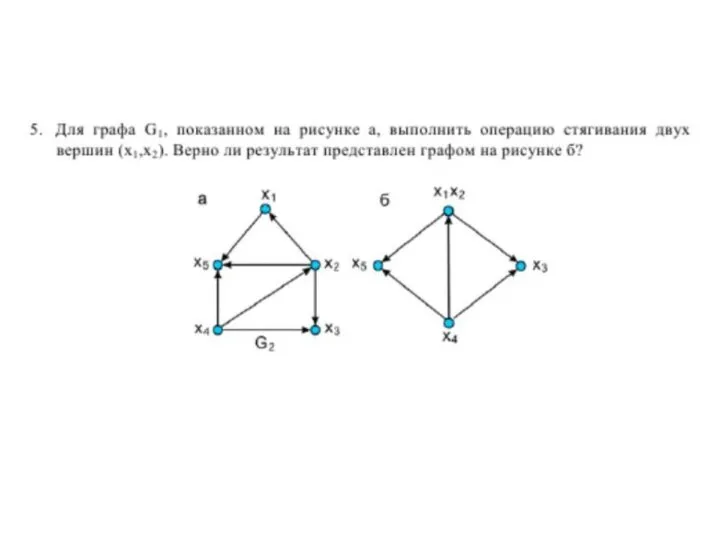
- 15. СТЯГИВАНИЕ вверху – стягивание дуги a1, внизу – дуг a1 , a6 и a7 Под стягиванием
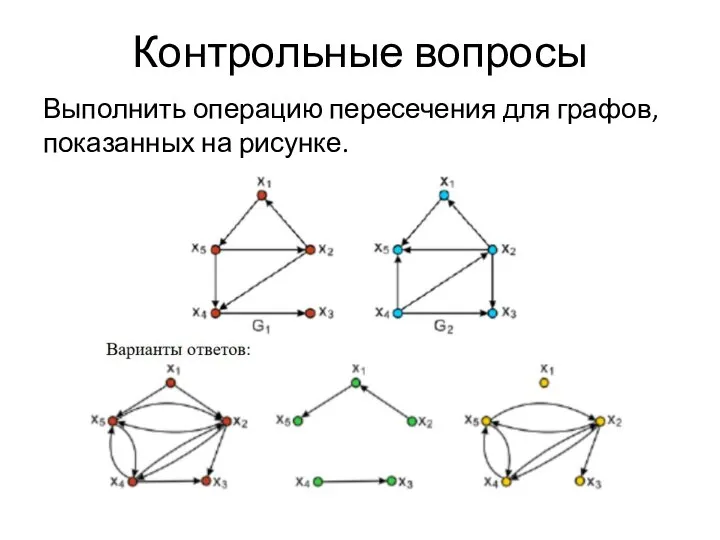
- 16. Контрольные вопросы Выполнить операцию пересечения для графов, показанных на рисунке.
- 17. Контрольные вопросы Выполнить операцию пересечения для графов, представленных матрицами смежности смежности.
- 25. Источники информации Программирование, компьютеры и сети https://progr-system.ru/
- 27. Скачать презентацию









 Психология девиантного поведения. Десоциализация личности и интернет в контексте психологии девиантного поведения
Психология девиантного поведения. Десоциализация личности и интернет в контексте психологии девиантного поведения Графический интерфейс
Графический интерфейс Обеспечение информационной безопасности детства
Обеспечение информационной безопасности детства Основы современных операционных систем
Основы современных операционных систем Миграция для Notes в Exchange
Миграция для Notes в Exchange Об’єктно-орієнтоване програмування. Лекція №0
Об’єктно-орієнтоване програмування. Лекція №0 Практикум овладения компьютером (технология) 3 класс
Практикум овладения компьютером (технология) 3 класс Решение задач с одномерным массивом
Решение задач с одномерным массивом Цель ведения аккаунта
Цель ведения аккаунта Профессия программист. Linus Torvalds
Профессия программист. Linus Torvalds c5f0a843-16d7-4791-875b-3b9c26b67276
c5f0a843-16d7-4791-875b-3b9c26b67276 You Tube
You Tube Аппаратное обеспечение персональных компьютеров
Аппаратное обеспечение персональных компьютеров Библиотечный урок Как найти книгу в книжном фонде?
Библиотечный урок Как найти книгу в книжном фонде? Программист. Билл Гейтс
Программист. Билл Гейтс Регистровая память. Регистры микропроцессора
Регистровая память. Регистры микропроцессора Розробка системи тестового контролю знань з навчальної дисципліни Ділова англійська мова
Розробка системи тестового контролю знань з навчальної дисципліни Ділова англійська мова Site Tour (2)
Site Tour (2)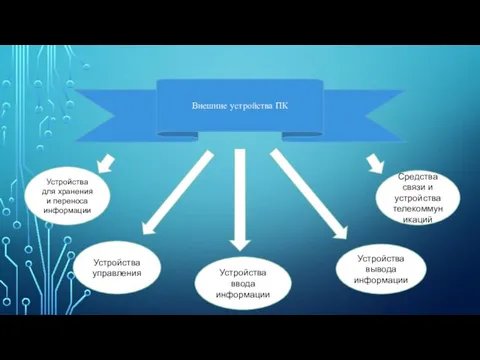 Внешние устройства ПК
Внешние устройства ПК Знакомство с новой лексикой
Знакомство с новой лексикой Проектирование и разработка веб-сервера с поддержкой FastCGI
Проектирование и разработка веб-сервера с поддержкой FastCGI Информационная безопасность
Информационная безопасность Основы программирования на языке Pascal
Основы программирования на языке Pascal Двоичное кодирование текста. 7 класс
Двоичное кодирование текста. 7 класс 5 2 ИОННАЯ ИМПЛАНТАЦИЯ
5 2 ИОННАЯ ИМПЛАНТАЦИЯ Анализ требований к программному обеспечению. Анализ и моделирование функциональной области внедрения программных систем
Анализ требований к программному обеспечению. Анализ и моделирование функциональной области внедрения программных систем Shopping Cart. Поиск товара
Shopping Cart. Поиск товара Информатика в лицах
Информатика в лицах