Содержание
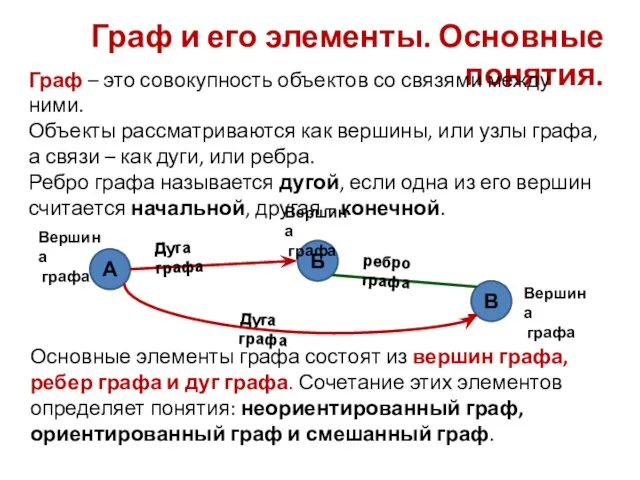
- 2. Граф и его элементы. Основные понятия. Граф – это совокупность объектов со связями между ними. Объекты
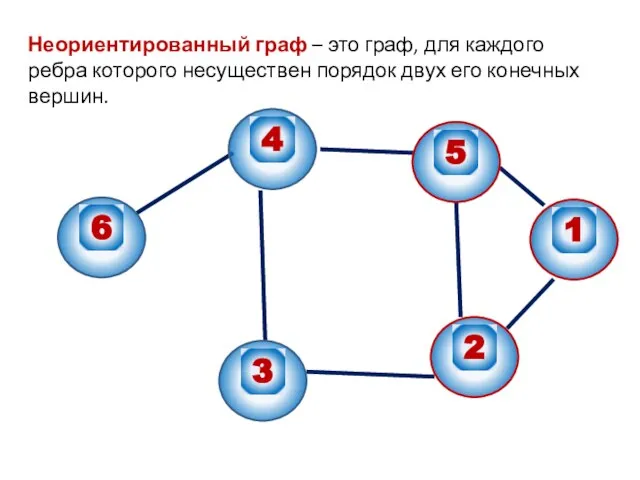
- 3. Неориентированный граф – это граф, для каждого ребра которого несуществен порядок двух его конечных вершин.
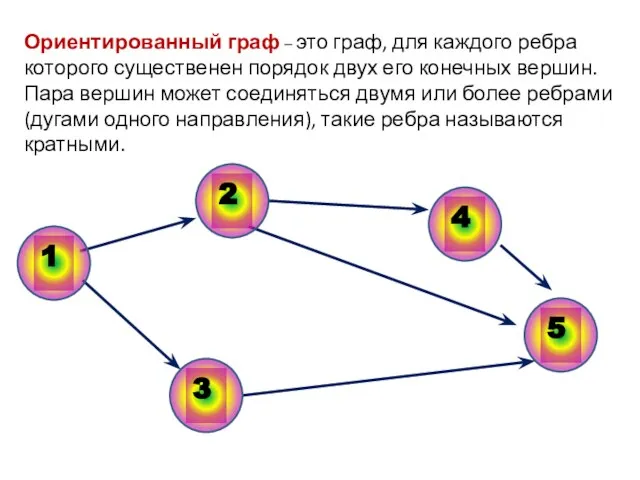
- 4. Ориентированный граф – это граф, для каждого ребра которого существенен порядок двух его конечных вершин. Пара
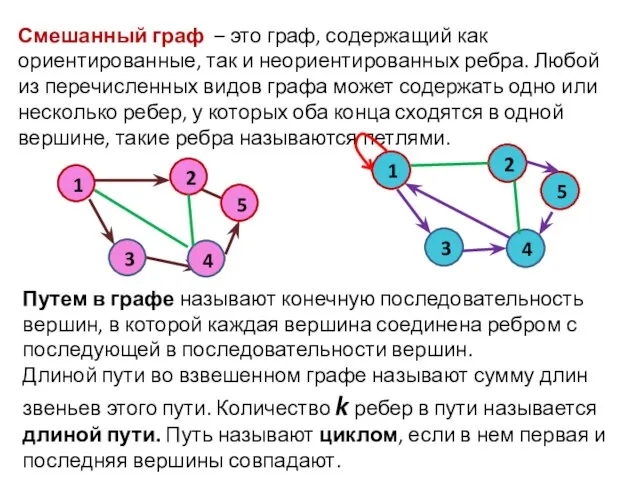
- 5. Смешанный граф – это граф, содержащий как ориентированные, так и неориентированных ребра. Любой из перечисленных видов
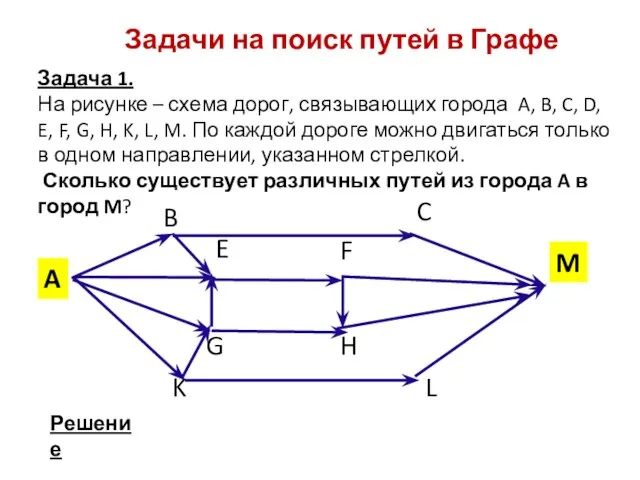
- 6. 12 Задачи на поиск путей в Графе Задача 1. На рисунке – схема дорог, связывающих города
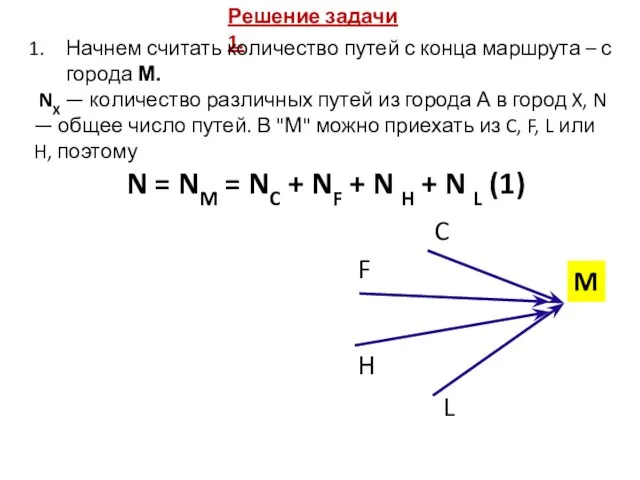
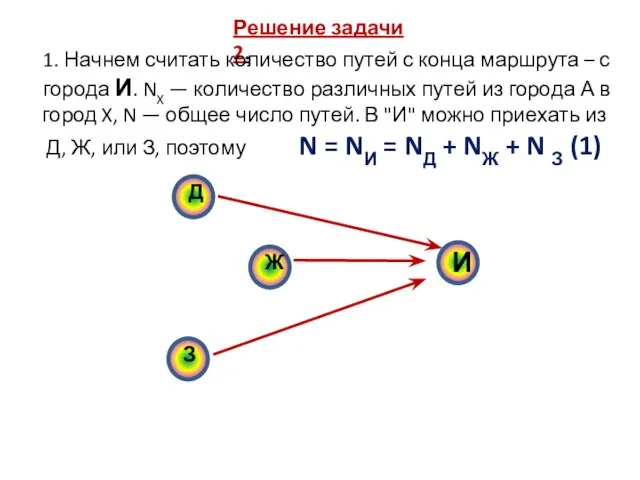
- 7. Решение задачи 1. Начнем считать количество путей с конца маршрута – с города М. NX —
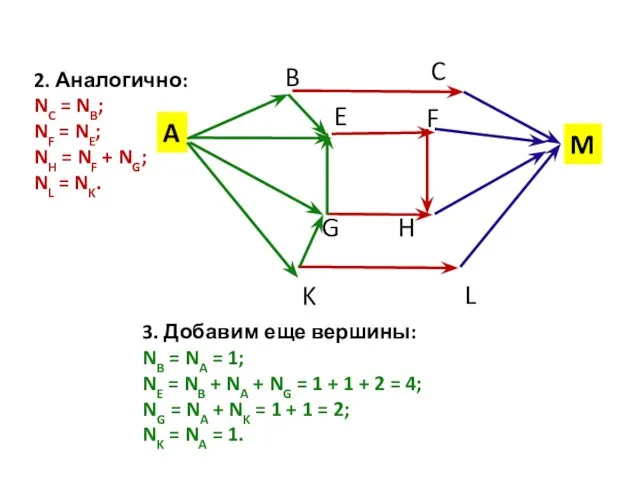
- 8. 2. Аналогично: NC = NB; NF = NE; NH = NF + NG; NL = NK.
- 9. 4. Преобразуем вершины: NC = NB = 1; NF = NE = 4; NH = NF
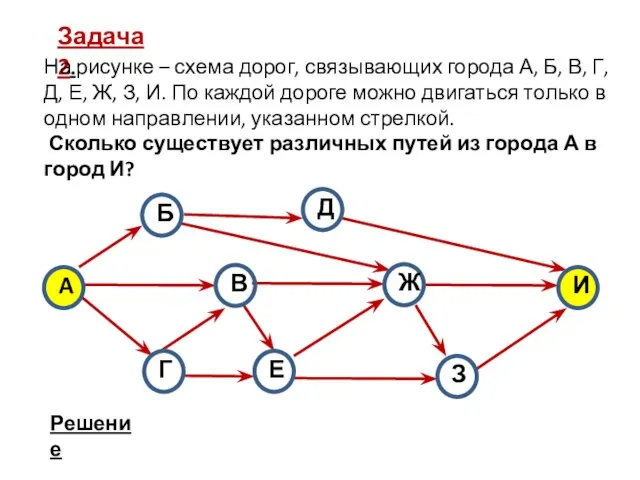
- 10. Задача 2. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж,
- 11. Решение задачи 2. 1. Начнем считать количество путей с конца маршрута – с города И. NX
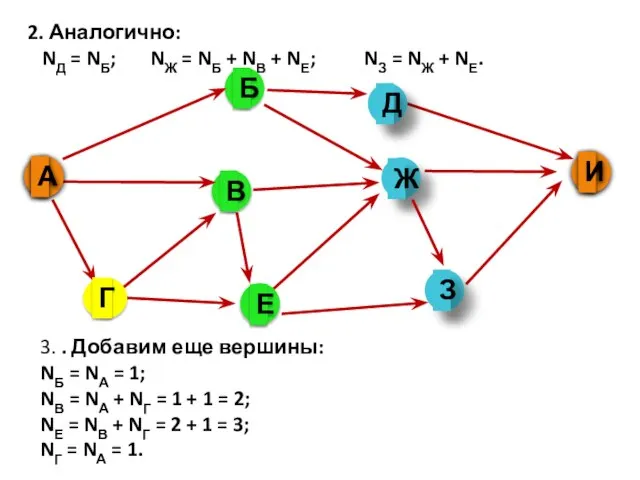
- 12. 2. Аналогично: NД = NБ; NЖ = NБ + NВ + NЕ; NЗ = NЖ +
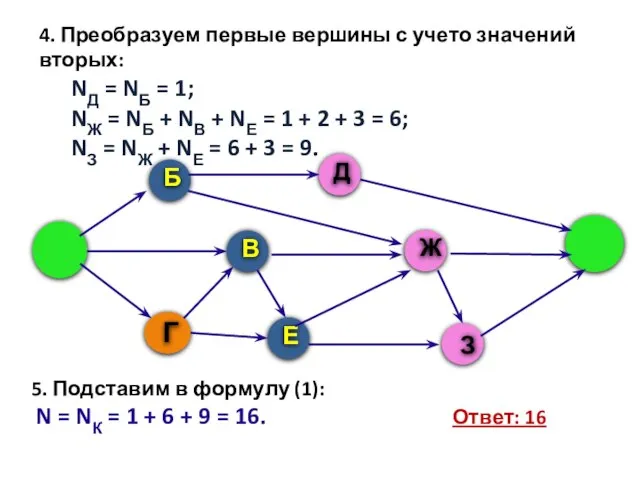
- 13. 4. Преобразуем первые вершины с учето значений вторых: NД = NБ = 1; NЖ = NБ
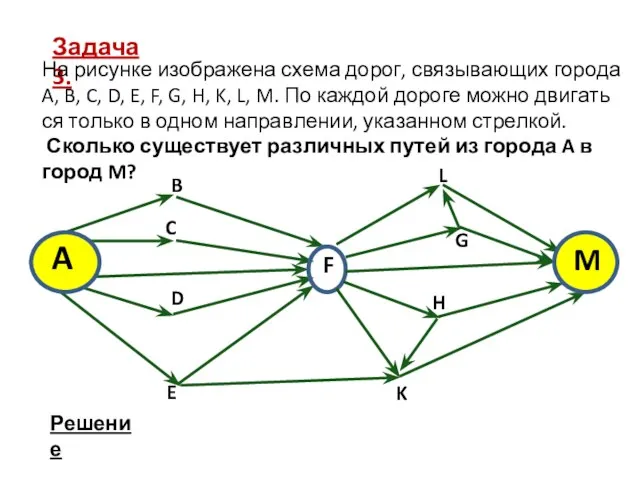
- 14. Задача 3. На рисунке изображена схема дорог, связывающих города A, B, C, D, E, F, G,
- 15. Решение задачи 3. 1. Начнем считать количество путей с конца маршрута — с города M. Пусть
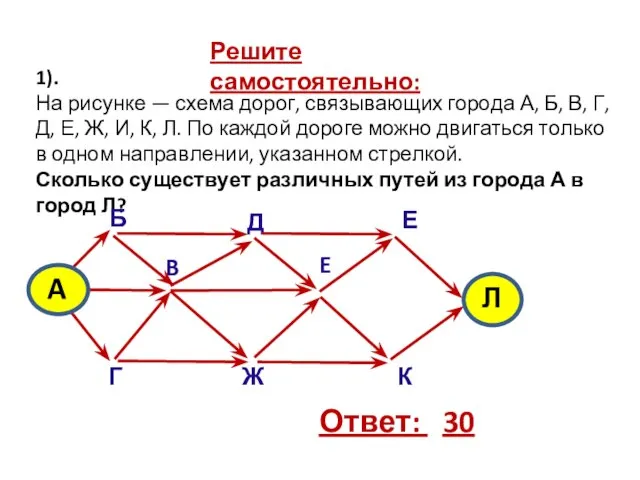
- 16. Решите самостоятельно: 1). На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е,
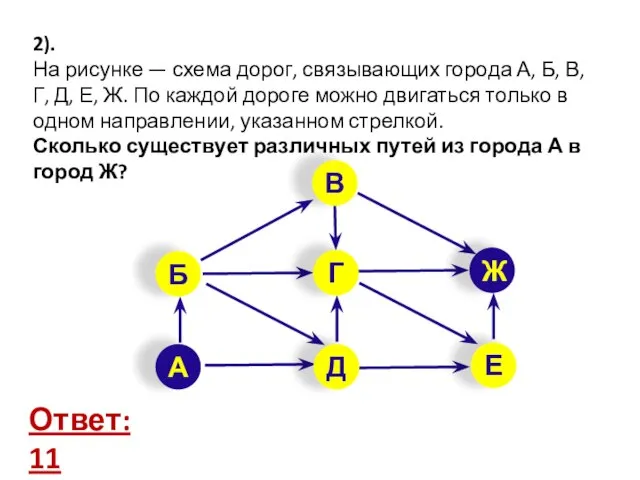
- 17. 2). На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж. По
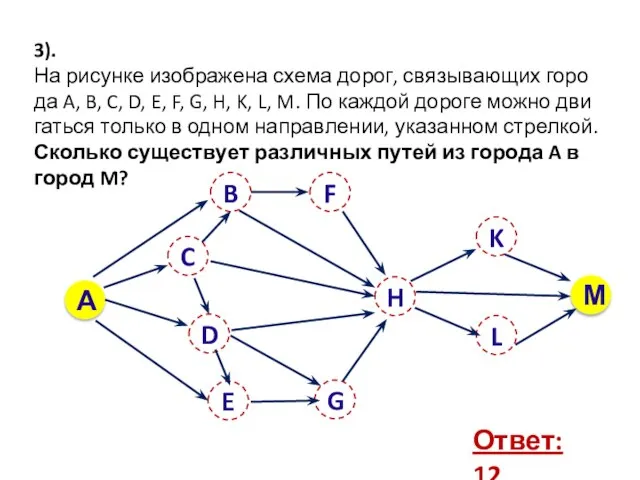
- 18. 3). На рисунке изображена схема дорог, связывающих города A, B, C, D, E, F, G, H,
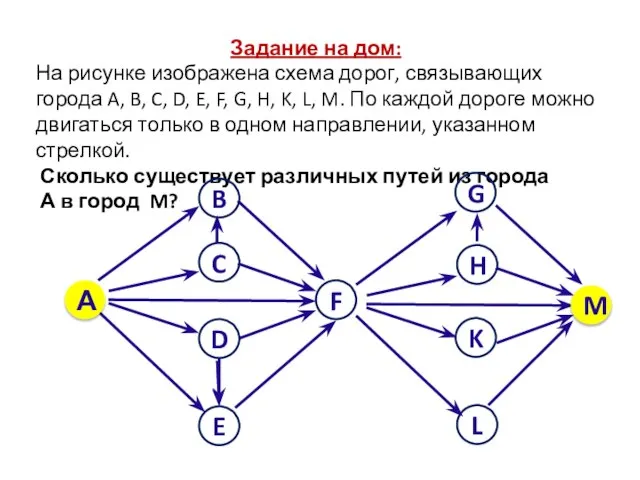
- 19. Задание на дом: На рисунке изображена схема дорог, связывающих города A, B, C, D, E, F,
- 21. Скачать презентацию


 Устройства ввода графической информации. Практическая работа № 8. Работаем с графическими фрагментами
Устройства ввода графической информации. Практическая работа № 8. Работаем с графическими фрагментами Объектно-ориентированное программирование. Лекция 4
Объектно-ориентированное программирование. Лекция 4 Вычислительные системы и сети
Вычислительные системы и сети 4 Двоичное кодирование
4 Двоичное кодирование Принц Персии. Игра
Принц Персии. Игра 21-1
21-1 Презентация
Презентация Тема+4.+Встроенный+язык
Тема+4.+Встроенный+язык Силометр
Силометр Интернет-сервисы по созданию видеороликов
Интернет-сервисы по созданию видеороликов Циклы. Исполнитель робот
Циклы. Исполнитель робот Онлайн-сервисы в профессиональной деятельности
Онлайн-сервисы в профессиональной деятельности Аналогичная закономерность. Часть 1. 3 класс
Аналогичная закономерность. Часть 1. 3 класс Перспективы работы оборудования ЗАО ЗЭТО в составе цифровых подстанций
Перспективы работы оборудования ЗАО ЗЭТО в составе цифровых подстанций Мужской стиль. Источники информации о моде
Мужской стиль. Источники информации о моде Обработка персональных данных. Семинар-задание
Обработка персональных данных. Семинар-задание Проект ERP
Проект ERP Художественно-техническое оформление издания
Художественно-техническое оформление издания Двоичная арифметика
Двоичная арифметика Кенгуру 2020. Математика для всех
Кенгуру 2020. Математика для всех Предпосылки создания и развития АСУ
Предпосылки создания и развития АСУ Дистанционные тренировки. Художественная гимнастика
Дистанционные тренировки. Художественная гимнастика Инструментальная система ARIS для моделирования бизнеса
Инструментальная система ARIS для моделирования бизнеса Пакеты прикладных программ
Пакеты прикладных программ Работа по вариантам 10 к 2 ( гугл - тест )
Работа по вариантам 10 к 2 ( гугл - тест ) Модели жизненного цикла
Модели жизненного цикла Инструкция по регистрации Coursera
Инструкция по регистрации Coursera