Слайд 2 Любая таблица идентификаторов состоит
из набора полей, количество которых равно числу различных

идентификаторов, найденных в исходной программе. В ней может храниться следующая информация:
для переменных:
имя; тип данных; область памяти;
для функций:
имя функции;
количество и типы формальных аргументов;
тип возвращаемого результата;
адрес кода функции.
Слайд 3Логарифмический поиск
Искомый символ сравнивается с элементом в середине таблицы ( (N +

1)/2).
Если этот элемент не является искомым, то просматривается только блок элементов, пронумерованных от 1 до (N + 1)/2 - 1, или блок элементов от (N + 1)/2 + 1 до N в зависимости от того, меньше или больше искомый элемент по сравнению с ранее найденным.
Так продолжается до тех пор, пока либо искомый элемент не будет найден, либо алгоритм дойдет до очередного блока, содержащего один или два элемента (с которыми можно выполнить прямое сравнение искомого элемента).
Слайд 4Алгоритм бинарного дерева
Первый идентификатор поместить в вершину дерева.
Шаг 1. Выбрать очередной

идентификатор из входного потока данных. Если его нет, построение дерева закончено.
Шаг 2. Сделать текущим узлом дерева корневую вершину.
Шаг 3. Сравнить очередной идентификатор с тем, что содержится в текущем узле дерева.
Шаг 4. Если очередной идентификатор меньше, то перейти к шагу 5, если равен – сообщить об ошибке и прекратить выполнение алгоритма, иначе – перейти к шагу 7.
Слайд 5Шаг 5. Если у текущего узла существует левая вершина, то сделать ее

текущим узлом и вернуться к шагу 3, иначе перейти к шагу 6.
Шаг 6. Создать новую вершину, поместить в нее очередной идентификатор, сделать эту новую вершину левой вершиной текущего узла, вернуться к шагу 1.
Шаг 7. Если у текущего узла существует правая вершина, то сделать ее текущим узлом и вернуться к шагу 3, иначе перейти к шагу 8.
Шаг 8. Создать новую вершину, поместить в нее очередной идентификатор, сделать эту новую вершину правой вершиной текущего узла и вернуться к шагу 1.
Слайд 6Пример
Gа, D1, M22, Е, А12, ВС, F
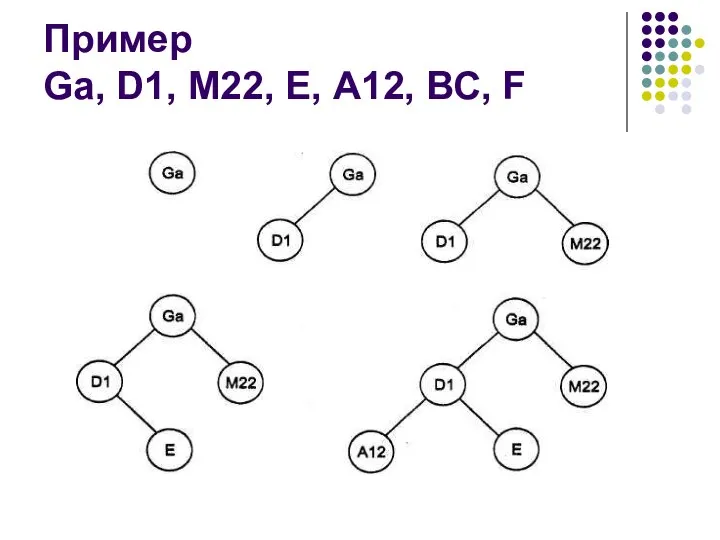
Слайд 8Поиск нужного элемента в дереве
Шаг 1. Сделать текущим узлом дерева корневую вершину.
Шаг

2. Сравнить искомый идентификатор с идентификатором, содержащимся в текущем узле дерева.
Шаг 3. Если идентификаторы совпадают, то искомый идентификатор найден, алгоритм завершен, иначе перейти к шагу 4.
Слайд 9Шаг 4. Если очередной идентификатор меньше, то перейти к шагу 5, иначе

– к шагу 6.
Шаг 5. Если у текущего узла существует левая вершина, то сделать ее текущим узлом и вернуться к шагу 2, иначе искомый идентификатор не найден, алгоритм завершен.
Шаг 6. Если у текущего узла существует правая вершина, то сделать ее текущим узлом и вернуться к шагу 2, иначе искомый идентификатор не найден, алгоритм завершен.
Слайд 10Хэш-функция
Хэш-функцией F называется некоторое отображение множества входных элементов R на множество целых

неотрицательных чисел
Хэш-адресация заключается в использовании значения, возвращаемого хэш-функцией, в качестве адреса ячейки из некоторого массива данных.
Тогда размер массива данных должен соответствовать области значений используемой хэш-функции.
Слайд 11Метод рехэширования
Шаг 1. Вычислить значение хэш-функции n = h(A) для нового

элемента А.
Шаг 2. Если ячейка по адресу n пустая, то поместить в нее элемент А и завершить алгоритм, иначе i= 1 и перейти к шагу 3.
Шаг 3. Вычислить ni = hi (A). Если ячейка по адресу ni пустая, то поместить в нее элемент А и завершить алгоритм, иначе перейти к шагу 4.
Шаг 4. Если n = ni то сообщить об ошибке и завершить алгоритм, иначе i = i + 1 и вернуться к шагу 3.
Слайд 12Поиск элемента в таблице идентификаторов
Шаг 1. Вычислить значение хэш-функции n =

h(A) для искомого элемента А.
Шаг 2. Если ячейка по адресу n пустая, то элемент не найден, алгоритм завершен, иначе сравнить имя элемента в ячейке n с именем искомого элемента А. Если они совпадают, элемент найден и алгоритм завершен, иначе i= 1, перейти к шагу 3.
Шаг 3. Вычислить ni = hi(A). Если ячейка по адресу ni пустая или n = ni то элемент не найден и алгоритм завершен, иначе сравнить имя элемента в ячейке ni с именем искомого элемента А. Если они совпадают, то элемент найден и алгоритм завершен, иначе i = i + 1 и повторить шаг 3.
Слайд 13Метод цепочек
Шаг 1. Во все ячейки хэш-таблицы поместить пустое значение, таблица идентификаторов

пуста, переменная FreePtr (указатель первой свободной ячейки) указывает на начало таблицы идентификаторов; i = 1.
Шаг 2. Вычислить значение хэш-функции ni для нового элемента Аi. Если ячейка хэш-таблицы по адресу ni пуста, то поместить в нее значение переменной FreePtr и перейти к шагу 5; иначе перейти к шагу 3.
Шаг 3. Положить j=1, выбрать из хэш-таблицы адрес ячейки таблицы идентификаторов mj и перейти к шагу 4.
Слайд 14Шаг 4. Для ячейки таблицы идентификаторов по адресу mj проверить значение поля

ссылки. Если оно пустое, то записать в него адрес из переменной FreePtr и перейти к шагу 5; иначе j= j + 1, выбрать из поля ссылки адрес mj и повторить шаг 4.
Шаг 5. Добавить в таблицу идентификаторов новую ячейку, записать в нее информацию для элемента Аi (поле ссылки должно быть пустым), в переменную FreePtr поместить адрес за концом добавленной ячейки. Если больше нет идентификаторов, которые надо разместить в таблице, то выполнение алгоритма закончено, иначе i = i + 1 и перейти к шагу 2.












 Открытое программное обеспечение на примере GNU и BSD
Открытое программное обеспечение на примере GNU и BSD Представление знаний в искусственном интеллекте
Представление знаний в искусственном интеллекте Разработка интерфейса приложения и разработка функционала приложения
Разработка интерфейса приложения и разработка функционала приложения Сравнительный анализ сайтов
Сравнительный анализ сайтов Тестирование, верификация и валидация ПО
Тестирование, верификация и валидация ПО Модели организации WLAN
Модели организации WLAN Логические основы компьютера
Логические основы компьютера Универсальность цифрового представления информации
Универсальность цифрового представления информации Введение в блокчейн
Введение в блокчейн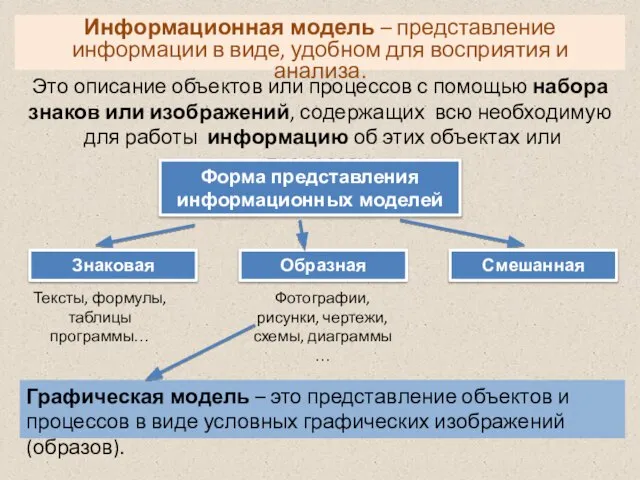 Информационная модель
Информационная модель Моделирование. Модели
Моделирование. Модели Руководство по использованию активов в сети Ethereum через платформу Flamingo
Руководство по использованию активов в сети Ethereum через платформу Flamingo Решение для интерент-магазинов
Решение для интерент-магазинов Original Character – Оригинальный Персонаж
Original Character – Оригинальный Персонаж Цифровые интерфейсы микропроцессорных терминалов
Цифровые интерфейсы микропроцессорных терминалов Программирование игр на Python
Программирование игр на Python Устройства ввода информации
Устройства ввода информации DigitalVender торговая платформа
DigitalVender торговая платформа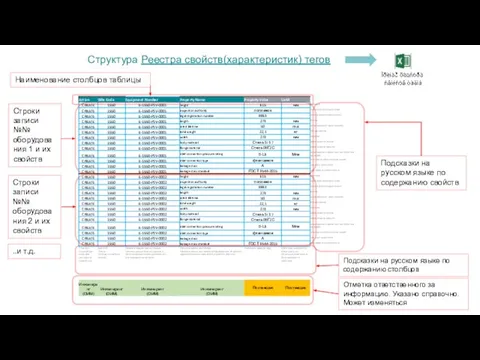 Реестры свойств тегов
Реестры свойств тегов История серии видеоигры: Warhammer
История серии видеоигры: Warhammer Компьютерные игры, которые основаны на книгах
Компьютерные игры, которые основаны на книгах Хранение информации. Создаем и сохраняем файлы
Хранение информации. Создаем и сохраняем файлы Школа::Кода Основы программирования на языке Python. 5 занятие
Школа::Кода Основы программирования на языке Python. 5 занятие Компьютерные вирусы
Компьютерные вирусы Объект. Задания к уроку
Объект. Задания к уроку 4IZ110 - Informační a komunikační technologie
4IZ110 - Informační a komunikační technologie Криптоанализ симметричных шифров
Криптоанализ симметричных шифров Реляционная модель данных и основы языка SQL. Семинар 1
Реляционная модель данных и основы языка SQL. Семинар 1