Содержание
- 2. Содержание Введение Непозиционные системы счисления Единичная Римская Позиционные системы счисления Десятичная Двоичная Задания
- 3. Введение Для записи информации о количестве объектов используются числа. Числа записываются с использование особых знаковых систем,
- 4. Система счисления – это знаковая система, в которой числа записываются по определенным правилам с помощью знаков
- 5. Непозиционные системы счисления В этой системе количественное значение цифры числа не зависит от того, в каком
- 6. Единичная («палочная») Период палеолита. 10-11 тысяч лет до н.э. - единицы - десятки - сотни =
- 7. Алфавитные системы Древняя Русь 1 2 3 4 5 6 7 8 9 10 «… В
- 8. Единичная система счисления Такая система записи чисел называется единичной, так как любое число образуется в ней
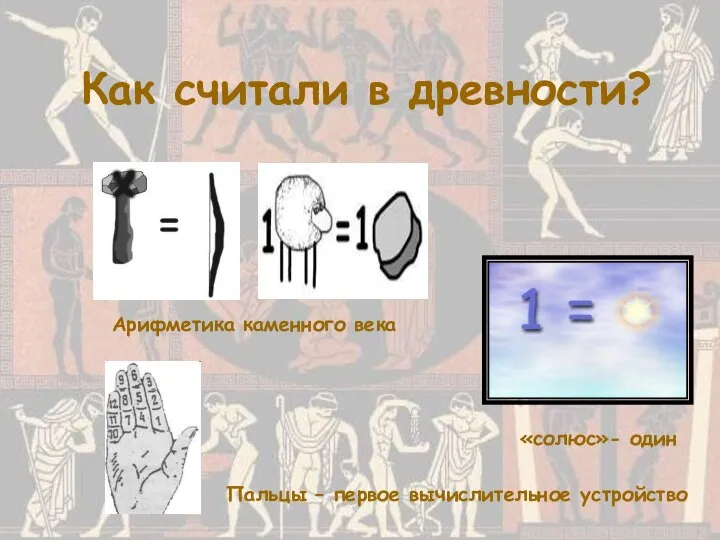
- 9. Как считали в древности? Арифметика каменного века «солюс»- один Пальцы – первое вычислительное устройство
- 10. Римская система счисления Самой распространенной из непозиционных систем счисления, которая сохранилась до наших дней, является римская
- 11. Римская система счисления В ее основе лежали знаки: Пример числа, записанного в римской системе счисления: От
- 12. Римская система счисления Величина числа в римской системе счисления определяется как сумма или разность цифр в
- 13. В римской системе количественное значение цифры не зависит от ее положения в числе. Например, в римском
- 14. При записи чисел в римской системе применяется правило: каждый меньший знак, поставленный слева от большего, вычитается
- 15. Позиционные системы счисления В позиционной системе счисления количественное значение каждой цифры числа зависит от того, в
- 16. Первая позиционная система счисления была придумана еще в Древнем Вавилоне, причем вавилонская нумерация была шестидесятеричная, т.е.
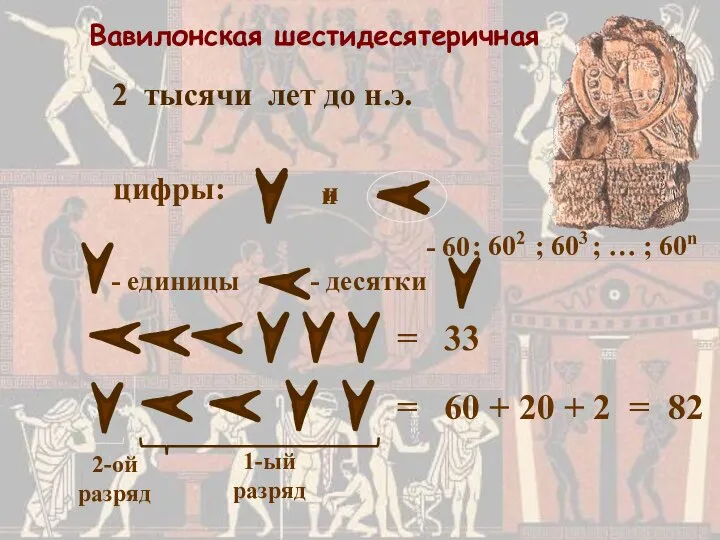
- 17. 2 тысячи лет до н.э. Вавилонская шестидесятеричная - единицы - десятки = 33 цифры: и 2-ой
- 18. В XIX веке довольно широкое распространение получила двенадцатеричная система счисления. До сих пор мы часто употребляем
- 19. Количество различных символов, используемых для изображения числа в позиционных системах счисления, называется основанием системы счисления.
- 20. В настоящее время наиболее распространенными позиционными системами счисления являются: Десятичная система (математика) Двоичная система (информатика) Содержание
- 21. Десятичная позиционная система счисления Десятичная система имеет алфавит цифр, который состоит из десяти всем известных, так
- 22. Десятичная позиционная система счисления Рассмотрим в качестве примера десятичное число 555. Цифра 5 встречается в числе
- 23. Двоичная система счисления Двоичная система имеет алфавит цифр, который состоит из двух цифр (0, 1) основание
- 25. Скачать презентацию




















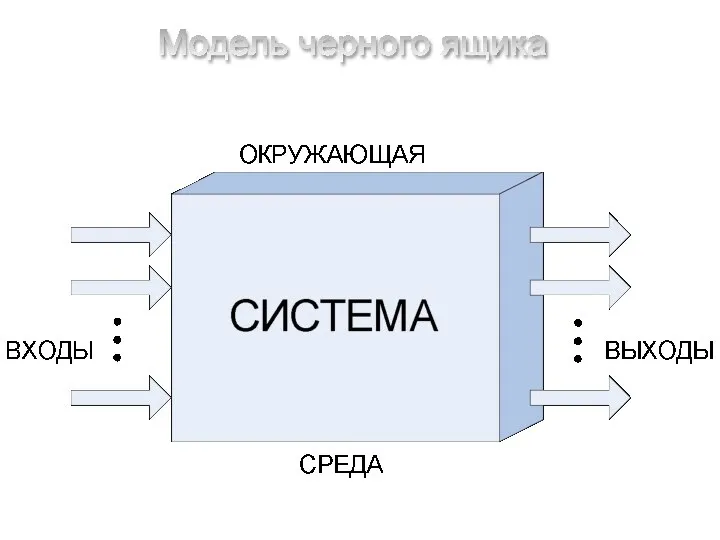 Модель черного ящика
Модель черного ящика Информационно-аналитическая система SCIENCE INDEX
Информационно-аналитическая система SCIENCE INDEX Графы. Общие понятия
Графы. Общие понятия Уровни программной конфигурации ПК
Уровни программной конфигурации ПК Временные ограничения цифровых схем
Временные ограничения цифровых схем Разработка программы для проектирования плана города
Разработка программы для проектирования плана города 5_Arrays_Lubchenko
5_Arrays_Lubchenko Vom Modell zur relationalen Datenbank
Vom Modell zur relationalen Datenbank Как воспользоваться электронной книгой. 1 - Виды форматов электронных книг 2- Программы для чтения электронных книг 3- Как скача
Как воспользоваться электронной книгой. 1 - Виды форматов электронных книг 2- Программы для чтения электронных книг 3- Как скача Integer Programming Example #1 - Combinatorics
Integer Programming Example #1 - Combinatorics Моделирование, формализация. Визуализация
Моделирование, формализация. Визуализация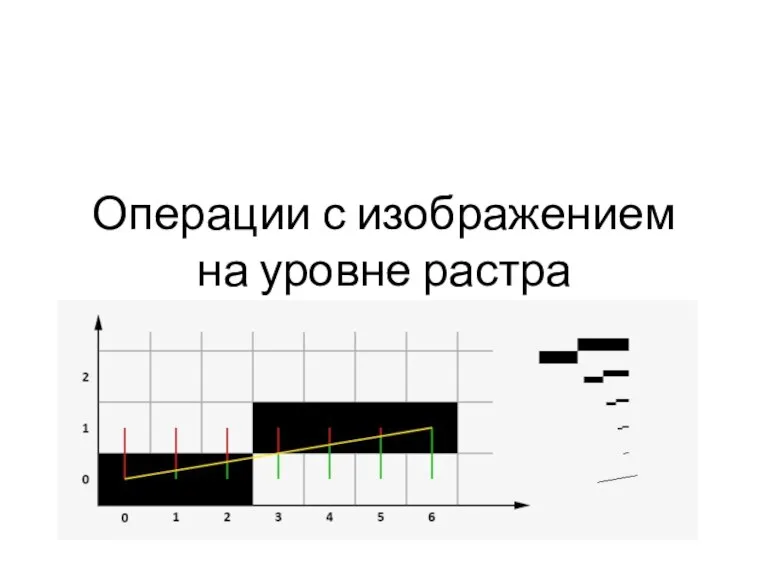 Операции с изображением на уровне растра
Операции с изображением на уровне растра Методы и средства сбора, передачи, хранения и поиска информации
Методы и средства сбора, передачи, хранения и поиска информации Контактный центр будущего
Контактный центр будущего Творческая работа на уроке информатики
Творческая работа на уроке информатики Электронные таблицы. Обработка числовой информации в электронных таблицах
Электронные таблицы. Обработка числовой информации в электронных таблицах Текст как информационный объект. Автоматизированные средства и технологии организации текста
Текст как информационный объект. Автоматизированные средства и технологии организации текста Естественные и искусственные источники информации. 3 класс
Естественные и искусственные источники информации. 3 класс Популяризация внутреннего туризма в РФ через внедрение современных медийных и репортажных технологий
Популяризация внутреннего туризма в РФ через внедрение современных медийных и репортажных технологий Информационная безопасность
Информационная безопасность Цикл с параметром в Pascal. Lazarus
Цикл с параметром в Pascal. Lazarus Как установить Пайчарм
Как установить Пайчарм Презентация на тему Охрана труда и техника безопасности
Презентация на тему Охрана труда и техника безопасности  Сетевой город. Образование
Сетевой город. Образование Написание программы
Написание программы Современные периферийные устройства виртуальной реальности
Современные периферийные устройства виртуальной реальности Компьютерные сети
Компьютерные сети Экспериментальное проектирование и процедура
Экспериментальное проектирование и процедура