Спортивное программирование. Занятие 1. Языковые средства, поразрядные операции, эффективность, структуры данных

Языковые средства
(ввод и вывод)
В большинстве олимпиадных задач для ввода и вывода используются стандартные потоки. В C++ стандартный поток ввода называется cin, а стандартный поток
вывода – cout. Можно также использовать
C-функции, например scanf и printf.

Языковые средства
(ввод и вывод)
Входными данными для программы обычно являются числа и строки, разделенные пробелами и знаками новой строки. Из потока cin они читаются следующим образом:
int a, b;
string x;
cin >> a >> b >> x;
Такой код работает в предположении, что элементы потока разделены хотя бы одним пробелом или знаком новой строки. Например, приведенный выше код может прочитать как входные данные:
123 456 monkey
так и входные данные:
123 456
monkey

Языковые средства
(ввод и вывод)
Поток cout используется для вывода:
#include
#include
using namespace std;
int main() {
int a = 123, b = 456;
string x = "monkey";
cout << a << " " << b << " " << x << "\n";
return 0;
}
Отметим, что знак новой строки "\n" работает быстрее, чем endl, потому что endl всегда сопровождается сбросом буфера.

Языковые средства
(ввод и вывод)
Ввод и вывод часто оказываются узкими местами программы. Чтобы повысить эффективность ввода-вывода, можно поместить в начало программы такие строки:
ios::sync_with_stdio(0);
cin.tie(0);

Языковые средства
(ввод и вывод)
C-функции scanf и printf – альтернатива стандартным потокам C++. Обычно они работают немного быстрее, но и использовать их сложнее.

Ввод и вывод
(вывод информации)
Функция printf() предназначена для форматированного вывода. Она переводит данные в символьное представление и выводит полученные изображения символов на экран. При этом у программиста имеется возможность форматировать данные, то есть влиять на их представление на экране.
Общая форма записи функции printf():
printf("СтрокаФорматов", объект1, объект2, ..., объектn);

Ввод и вывод
(вывод информации)
СтрокаФорматов состоит из следующих элементов:
управляющих символов;
текста, представленного для непосредственного вывода;
форматов, предназначенных для вывода значений переменных различных типов.
Объекты могут отсутствовать.

Ввод и вывод
(вывод информации)
Управляющие символы не выводятся на экран, а управляют расположением выводимых символов. Отличительной чертой управляющего символа является наличие обратного слэша ‘\’ перед ним.
Основные управляющие символы:
‘\n’ – перевод строки;
‘\t’ – горизонтальная табуляция;
‘\v’ – вертикальная табуляция;
‘\b’ – возврат на символ;
‘\r’ – возврат на начало строки;
‘\a’ – звуковой сигнал.

Ввод и вывод
(вывод информации)
Форматы нужны для того, чтобы указывать вид, в котором информация будет выведена на экран. Отличительной чертой формата является наличие символа процент ‘%’ перед ним:
%d – целое число типа int со знаком в десятичной системе счисления;
%u – целое число типа unsigned int;
%x – целое число типа int со знаком в шестнадцатеричной системе счисления;
%o – целое число типа int со знаком в восьмеричной системе счисления;
%hd – целое число типа short со знаком в десятичной системе счисления;
%hu – целое число типа unsigned short;
%hx – целое число типа short со знаком в шестнадцатеричной системе счисления;

Ввод и вывод
(вывод информации)
%ld – целое число типа long int со знаком в десятичной системе счисления;
%lu – целое число типа unsigned long int;
%lx – целое число типа long int со знаком в шестнадцатеричной системе счисления;
%f – вещественный формат (числа с плавающей точкой типа float);
%lf – вещественный формат двойной точности (числа с плавающей точкой типа double);
%e – вещественный формат в экспоненциальной форме (числа с плавающей точкой типа float в экспоненциальной форме);
%c – символьный формат;
%s – строковый формат.

Ввод и вывод
(вывод информации)
Строка форматов содержит форматы для вывода значений. Каждый формат вывода начинается с символа %. После строки форматов через запятую указываются имена переменных, которые необходимо вывести.
Количество символов % в строке формата должно совпадать с количеством переменных для вывода. Тип каждого формата должен совпадать с типом переменной, которая будет выводиться на это место. Замещение форматов вывода значениями переменных происходит в порядке их следования.

Ввод и вывод
(вывод информации)
#include
using namespace std;
int main() {
int a = 5;
float x = 2.78;
printf("a=%d\n", a);
printf("x=%f\n", x);
getchar();
return 0;
}
Результат работы программы
a=5
x=2.780000

Ввод и вывод
(вывод информации)
Тот же самый код может быть представлен с использованием одного вызова printf:
#include
using namespace std;
int main() {
int a = 5;
float x = 2.78;
printf("a=%d\nx=%f\n", a, x);
getchar();
return 0;
}

Ввод и вывод
(табличный вывод)
При указании формата можно явным образом указать общее количество знакомест и количество знакомест, занимаемых дробной частью:
#include
using namespace std;
int main() {
float x = 1.2345;
printf("x=%10.5f\n", x);
getchar();
return 0;
}
Результат выполнения
x= 1.23450

Ввод и вывод
(табличный вывод)
В приведенном примере 10 – общее количество знакомест, отводимое под значение переменной; 5 – количество позиций после разделителя целой и дробной части (после десятичной точки). В указанном примере количество знакомест в выводимом числе меньше 10, поэтому свободные знакоместа слева от числа заполняются пробелами. Такой способ форматирования часто используется для построения таблиц.

Ввод и вывод
(ввод информации)
Функция форматированного ввода данных с клавиатуры scanf() выполняет чтение данных, вводимых с клавиатуры, преобразует их во внутренний формат и передает вызывающей функции. При этом программист задает правила интерпретации входных данных с помощью спецификаций форматной строки.
Общая форма записи функции scanf():
scanf("CтрокаФорматов", адрес1, адрес2,...);

Ввод и вывод
(ввод информации)
Строка форматов аналогична функции printf().
Для формирования адреса переменной используется символ амперсанд ‘&’:
адрес = &объект.
Строка форматов и список аргументов для функции обязательны.

Ввод и вывод
(ввод информации)
#define _CRT_SECURE_NO_WARNINGS // для возможности использования scanf
#include
using namespace std;
int main() {
float y;
system("chcp 1251"); // переходим в консоли на русский язык
system("cls"); // очищаем окно консоли
printf("Введите y: "); // выводим сообщение
scanf("%f", &y); // вводим значения переменной y
printf("Значение переменной y=%f", y); // выводим значение переменной y
getchar(); getchar();
return 0;
}
Результат работы программы:
Введите y: 1.345
Значение переменной y=1.345000

Ввод и вывод
(ввод информации)
Функция scanf() является функцией незащищенного ввода, т.к. появилась она в ранних версиях языка Си. Поэтому чтобы разрешить работу данной функции в современных компиляторах необходимо в начало программы добавить строчку
#define _CRT_SECURE_NO_WARNINGS

Ввод и вывод
(ввод информации)
Другой вариант – воспользоваться функцией защищенного ввода scanf_s(), которая появилась несколько позже, но содержит тот же самый список параметров.
#include
using namespace std;
int main() {
int a;
printf("a = ");
scanf_s("%d", &a);
printf("a = %d", a);
getchar(); getchar();
return 0;
}

Языковые средства
(ввод и вывод)
Иногда программа должна прочитать целую входную строку, быть может, содержащую пробелы. Это можно сделать с помощью функции getline:
#include
#include
using namespace std;
int main() {
string s;
getline(cin, s);
return 0;
}

Языковые средства
(ввод и вывод)
Если объем данных заранее неизвестен, то полезен такой цикл:
while (cin >> x) {
// код
}
Этот цикл читает из стандартного ввода элементы один за другим, пока входные данные не закончатся.

Языковые средства
(ввод и вывод)
В некоторых олимпиадных системах для ввода и вывода используются файлы. В таком случае есть простое решение: писать код так, будто работаешь со стандартными потоками, но в начало программы добавить такие строки:
freopen("input.txt", "r", stdin);
freopen("output.txt", "w", stdout);
После этого программа будет читать данные из файла «input.txt», а записывать в файл «output.txt».

Языковые средства
(работа с числами)
Целые числа. Из целых типов в олимпиадном программировании чаще всего используется int – 32-разрядный тип, принимающий значения из диапазона
-231…231 - 1 (приблизительно
-2 · 109…2 · 109). Если типа int недостаточно, то можно взять 64-разрядный тип long long. Диапазон его значений -263…263 - 1 (приблизительно -9 · 1018…9 · 1018).

Языковые средства
(работа с числами)
Ниже определена переменная типа long long:
long long x = 123456789123456789LL;
Суффикс LL означает, что число имеет тип long long.

Языковые средства
(работа с числами)
Типичная ошибка при использовании типа long long возникает, когда где-то в программе встречается еще и тип int. Например, в следующем коде есть тонкая ошибка:
int a = 123456789;
long long b = a * a;
cout << b << "\n"; // -1757895751
Хотя переменная b имеет тип long long, оба сомножителя в выражении a*a имеют тип int, поэтому тип результата тоже int. Из-за этого значение b оказывается неверным. Проблему можно решить, изменив тип a на long long или изменив само выражение на (long long)a*a.

Языковые средства
(работа с числами)
Арифметика по модулю. Иногда ответом является очень большое число, но достаточно вывести результат «по модулю m», т. е. остаток от деления на m (например, «7 по модулю 109»). Идея в том, что даже когда истинный ответ очень велик, типов int и long long все равно достаточно.

Языковые средства
(работа с числами)
Остаток x от деления на m обозначается
x mod m. Например, 17 mod 5 = 2, поскольку
17 = 3 · 5 + 2. Важные свойства остатков выражаются следующими формулами:
(a + b) mod m = (a mod m + b mod m) mod m;
(a − b) mod m = (a mod m − b mod m) mod m;
(a · b) mod m = (a mod m · b mod m) mod m.
Это значит, что можно брать остаток после каждой операции, поэтому числа никогда не станут слишком большими.

Языковые средства
(работа с числами)
Например, следующий код вычисляет n! (n факториал) по модулю m:
long long x = 1;
for (int i = 1; i <= n; i++) {
x = (x * i) % m;
}
cout << x << "\n";

Языковые средства
(работа с числами)
Обычно хочется, чтобы остаток находился в диапазоне 0…m − 1. Но в C++ и в других языках остаток от деления отрицательного числа равен нулю или отрицателен. Чтобы не возникали отрицательные остатки, можно поступить следующим образом: сначала вычислить остаток, а если он отрицателен, прибавить m:
x = x % m;
if (x < 0) x += m;
Но это стоит делать, только если в программе встречается операция вычитания, так что остаток может стать отрицательным.

Языковые средства
(работа с числами)
Числа с плавающей точкой. В большинстве олимпиадных задач целых чисел достаточно, но иногда возникает потребность в числах с плавающей точкой. В C++ наиболее полезен 64-разрядный тип double.

Языковые средства
(работа с числами)
Требуемая точность ответа обычно указывается в формулировке задачи. Проще всего для вывода ответа использовать функцию printf и указать количество десятичных цифр в форматной строке. Например, следующий код печатает значение x с 9 цифрами после запятой:
printf("%.9f\n", x);

Языковые средства
(работа с числами)
С использованием чисел с плавающей точкой связана одна сложность: некоторые числа невозможно точно представить в таком формате, поэтому неизбежны ошибки округления. Например, в следующем коде получается значение x, немного меньшее 1, тогда как правильное значение равно в точности 1.
double x = 0.3 * 3 + 0.1;
printf("%.20f\n", x); // 0.99999999999999988898

Языковые средства
(работа с числами)
Числа с плавающей точкой рискованно сравнивать с помощью оператора ==, потому что иногда равные значения оказываются различны из-за ошибок округления. Более правильно считать, что два числа равны, если разность между ними меньше ε, где ε мало. Например, в следующем коде ε = 10−9:
if (abs(a - b) < 1e-9) {
// a и b равны
}

Языковые средства
(работа с числами)
Хотя числа с плавающей точкой, вообще говоря, не точны, не слишком большие целые числа представляются точно. Так, тип double позволяет точно представить все целые числа, по абсолютной величине не большие 253.

Языковые средства
(сокращение кода)
Имена типов. Ключевое слово typedef позволяет сопоставить типу данных короткое имя. Например, имя long long слишком длинное, поэтому можно определить для него короткий псевдоним ll:
typedef long long ll;

Языковые средства
(сокращение кода)
После этого код
long long a = 123456789;
long long b = 987654321;
cout << a * b << "\n";
можно немного сократить:
ll a = 123456789;
ll b = 987654321;
cout << a * b << "\n";

Языковые средства
(сокращение кода)
Ключевое слово typedef применимо и к более сложным типам. Например, ниже вектору целых чисел сопоставляется имя vi, а паре двух целых чисел – тип pi.
typedef vector
vi;
typedef pair
pi;

Языковые средства
(сокращение кода)
Макросы. Еще один способ сократить
код – макросы. Макрос говорит, что определенные строки кода следует подменить до компиляции. В C++ макросы определяются с помощью ключевого слова #define.

Языковые средства
(сокращение кода)
Например, можно определить следующие макросы:
#define F first
#define S second
#define PB push_back
#define MP make_pair

Языковые средства
(сокращение кода)
После чего код
v.push_back(make_pair(y1, x1));
v.push_back(make_pair(y2, x2));
int d = v[i].first + v[i].second;
можно сократить до:
v.PB(MP(y1, x1));
v.PB(MP(y2, x2));
int d = v[i].F + v[i].S;

Языковые средства
(сокращение кода)
У макроса могут быть параметры, что позволяет сокращать циклы и другие структуры. Например, можно определить такой макрос:
#define REP(i, a, b) for (int i = a; i <= b; i++)

Языковые средства
(сокращение кода)
После этого код
for (int i = 1; i <= n; i++) {
search(i);
}
можно сократить следующим образом:
REP (i, 1, n) {
search(i);
}

Поразрядные операции
В программировании n-разрядное целое число хранится в виде двоичного числа, содержащего n бит. Например, тип int в C++ 32-разрядный, т. е. любое число типа int содержит 32 бита. Так, двоичное представление числа 43 типа int имеет вид
00000000000000000000000000101011.

Поразрядные операции
Биты в этом представлении нумеруются справа налево. Преобразование двоичного представления bk … b2b1b0 в десятичное число производится по формуле
bk2k + … + b222 + b121 + b020.
Например:
1 · 25 + 1 · 23 + 1 · 21 + 1 · 20 = 43.

Поразрядные операции
Двоичное представление числа может быть со знаком и без знака. Обычно используется представление со знаком, позволяющее представить положительные и отрицательные числа. n-разрядная переменная со знаком может содержать любое целое число в диапазоне от −2n−1 до 2n−1 − 1. Например, тип int в C++ знаковый, поэтому переменная типа int может содержать любое целое число от −231 до 231 − 1.

Поразрядные операции
Первый разряд в представлении со знаком содержит знак числа (0 для неотрицательных чисел, 1 – для отрицательных), а остальные n − 1
разрядов – абсолютную величину числа. Используется дополнительный код, т. е. для получения противоположного числа нужно сначала инвертировать все его биты, а затем прибавить к результату единицу. Например, двоичное представление числа –43 типа int имеет вид
11111111111111111111111111010101.

Поразрядные операции
Представление без знака позволяет представить только неотрицательные числа, но верхняя граница диапазона больше.
n-разрядная переменная без знака может содержать любое целое число от 0 до 2n − 1. Например, в C++ переменная типа unsigned int может содержать любое целое число от 0 до 232 − 1.

Поразрядные операции
Между обоими представлениям существует связь: число со знаком –x равно числу без знака 2n − x. К примеру, следующая программа показывает, что число со знаком x = −43 равно числу без знака y = 232 − 43:
int x = -43;
unsigned int y = x;
cout << x << "\n"; // -43
cout << y << "\n"; // 4294967253

Поразрядные операции
Если число больше верхней границы допустимого диапазона, то возникает переполнение. В представлении со знаком число, следующее за 2n−1 – 1, равно −2n−1, а в представлении без знака за 2n − 1 следует 0. Рассмотрим следующий код:
int x = 2147483647;
cout << x << "\n"; // 2147483647
x++;
cout << x << "\n"; // -2147483648
Первоначально x принимает значение 231 − 1. Это наибольшее значение, которое можно сохранить в переменной типа int, поэтому следующее за 231 − 1 значение равно −231.

Поразрядные операции
Операция И. Результатом операции И x & y является число, двоичное представление которого содержит единицы в тех позициях, на которых в представлениях x и y находятся единицы. Например, 22 & 26 = 18, поскольку
10110 (22)
& 11010 (26)
= 10010 (18)
С помощью операции И можно проверить, является ли число x четным, т. к. x & 1 = 0, если x четно, и x & 1 = 1, если x нечетно. Вообще, x нацело делится на 2k, если x & (2k − 1) = 0.

Поразрядные операции
Операция ИЛИ. Результатом операции ИЛИ x | y является число, двоичное представление которого содержит единицы в тех позициях, на которых хотя бы в одном из представлений x и y находятся единицы. Например, 22 | 26 = 30, поскольку
10110 (22)
| 11010 (26)
= 11110 (30)

Поразрядные операции
Операция ИСКЛЮЧАЮЩЕЕ ИЛИ. Результатом операции ИСКЛЮЧАЮЩЕЕ ИЛИ x ^ y является число, двоичное представление которого содержит единицы в тех позициях, на которых ровно в одном из представлений x и y находятся единицы. Например, 22 ^ 26 = 12, поскольку
10110 (22)
ˆ 11010 (26)
= 01100 (12)

Поразрядные операции
Операция НЕ. Результатом операции НЕ ~x является число, в двоичном представлении которого все биты x инвертированы. Справедлива формула ~x = −x – 1, например ~29 = −30. Результат операции НЕ на битовом уровне зависит от длины двоичного представления, поскольку инвертируются все биты. Например, в случае
32-разрядных чисел типа int имеем:
x = 29 00000000000000000000000000011101
~x = −30 11111111111111111111111111100010

Поразрядные операции
Поразрядный сдвиг. Операция поразрядного сдвига влево x << k дописывает в конец числа k нулей, а операция поразрядного сдвига вправо
x >> k удаляет k последних бит. Например,
14 << 2 = 56, поскольку двоичные представления 14 и 56 равны соответственно 1110 и 111000. Аналогично 49 >> 3 = 6, потому что 49 и 6 в двоичном виде равны соответственно 110001 и 110. Отметим, что операция x << k соответствует умножению x на 2k, а x >> k – делению x на 2k с последующим округлением с недостатком до целого.

Поразрядные операции
Битовые маски. Битовой маской называется число вида 1 << k, содержащее в позиции k единицу, а во всех остальных позициях – нули. Такую маску можно использовать для выделения одиночных битов. В частности, k-й бит числа равен единице тогда и только тогда, когда
x & (1 << k) не равно нулю. В следующем фрагменте печатается двоичное представление числа x типа int:
for (int k = 31; k >= 0; k--) {
if (x & (1 << k)) cout << "1";
else cout << "0";
}

Поразрядные операции
Аналогичным образом можно модифицировать отдельные биты числа. Выражение x | (1 << k) устанавливает k-й бит x в единицу, выражение
x & ~(1 << k) сбрасывает k-й бит x в нуль, а выражение x ˆ (1 << k) инвертирует k-й бит x. Далее выражение x & (x − 1) сбрасывает последний единичный бит x в нуль, а выражение x & −x сбрасывает в нуль все единичные биты, кроме последнего. Выражение x | (x − 1) инвертирует все биты после последнего единичного. Наконец, положительное число x является степенью двойки тогда и только тогда, когда x & (x − 1) = 0.

Поразрядные операции
При работе с битовыми масками нужно помнить, что 1< тип int. Самый простой способ создать битовую маску типа long long – написать 1LL<

Эффективность
(временная сложность)
Временная сложность алгоритма – это оценка того, сколько времени будет работать алгоритм при заданных входных данных. Зная временную сложность, зачастую можно сказать, достаточно ли алгоритм быстрый для решения задачи, даже не реализуя его.

Эффективность
(временная сложность)
Для описания временной сложности применяется нотация O(…), где многоточием представлена некоторая функция. Обычно буквой n обозначается размер входных данных. Например, если на вход подается массив чисел, то n – это размер массива, а если строка, то n – длина строки.

Эффективность
(временная сложность)
Если код включает только линейную последовательность команд, как, например, показанный ниже, то его временная сложность равна O(1).
a++;
b++;
c = a + b;

Эффективность
(временная сложность)
Временная сложность цикла оценивает число выполненных итераций. Например, временная сложность следующего кода равна O(n), поскольку код внутри цикла выполняется n раз. При этом предполагается, что многоточием «…» обозначен код с временной сложностью O(1).
for (int i = 1; i <= n; i++) {
...
}

Эффективность
(временная сложность)
Временная сложность следующего кода равна O(n2):
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
...
}
}

Эффективность
(временная сложность)
Временная сложность следующего кода равна O(n2):
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
...
}
}
Вообще, если имеется k вложенных циклов и в каждом цикле перебирается n значений, то временная сложность равна O(nk).

Эффективность
(временная сложность)
Временная сложность не сообщает, сколько точно раз выполняется код внутри цикла, она показывает лишь порядок величины, игнорируя постоянные множители. В примерах ниже код внутри цикла выполняется 3n, n + 5 и ⌈n/2⌉ раз, но временная сложность в каждом случае равна O(n).
for (int i = 1; i <= 3 * n; i++) {
...
}
for (int i = 1; i <= n + 5; i++) {
...
}
for (int i = 1; i <= n; i += 2) {
...
}

Эффективность
(временная сложность)
С другой стороны, временная сложность следующего кода равна O(n2), поскольку код внутри цикла выполняется 1 + 2 + … + n = ½(n2 + n) раз.
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= i; j++) {
...
}
}

Эффективность
(временная сложность)
Если алгоритм состоит из нескольких последовательных частей, то общая временная сложность равна максимуму из временных сложностей отдельных частей, т. е. самая медленная часть является узким местом. Так, следующий код состоит из трех частей с временной сложностью O(n), O(n2) и O(n). Поэтому общая временная сложность равна O(n2).
for (int i = 1; i <= n; i++) {
...
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
...
}
}
for (int i = 1; i <= n; i++) {
...
}

Эффективность
(временная сложность)
Иногда временная сложность зависит от нескольких факторов, поэтому формула включает несколько переменных. Например, временная сложность следующего кода равна O(nm):
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
...
}
}

Эффективность
(временная сложность)
Временная сложность рекурсивной функции зависит от того, сколько раз она вызывается, и от временной сложности одного вызова. Общая временная сложность равна произведению того и другого. Рассмотрим, к примеру, следующую функцию:
void f(int n) {
if (n == 1) return;
f(n - 1);
}
Вызов f(n) приводит к n вызовам функций, и временная сложность каждого вызова равна O(1), поэтому общая временная сложность равна O(n).

Эффективность
(временная сложность)
В качестве еще одного примера рассмотрим следующую функцию:
void g(int n) {
if (n == 1) return;
g(n - 1);
g(n - 1);
}
Что происходит, когда эта функция вызывается с параметром n? Сначала она будет дважды вызвана с параметром n−1, затем четыре раза с параметром n−2, потом восемь раз с параметром n−3 и т. д. Вообще, будет 2k вызовов с параметром n–k, где k = 0, 1, …, n−1. Таким образом, общая временная сложность равна
1 + 2 + 4 + … + 2n−1 = 2n − 1 = O(2n).

Эффективность
(временная сложность)
Далее перечислены часто встречающиеся оценки временной сложности алгоритмов.
O(1) Время работы алгоритма с постоянным временем не зависит от размера входных данных. Типичным примером может служить явная формула, по которой вычисляется ответ.

Эффективность
(временная сложность)
O(log n) В логарифмическом алгоритме размер входных данных на каждом шаге обычно уменьшается вдвое. Время работы зависит от размера входных данных логарифмически, поскольку log2 n – это сколько раз нужно разделить n на 2, чтобы получить 1. Отметим, что основание логарифма во временной сложности не указывается.

Эффективность
(временная сложность)

Эффективность
(временная сложность)
O(n) Линейный алгоритм перебирает входные данные постоянное число раз. Зачастую это наилучшая возможная временная сложность, потому что обычно, чтобы получить ответ, необходимо обратиться к каждому элементу хотя бы один раз.

Эффективность
(временная сложность)
O(n log n) Такая временная сложность часто означает, что алгоритм сортирует входные данные, поскольку временная сложность эффективных алгоритмов сортировки равна O(n log n). Есть и другая возможность – в алгоритме используется структура данных, для которой каждая операция занимает время O(log n).

Эффективность
(временная сложность)
O(n2) Квадратичный алгоритм нередко содержит два вложенных цикла. Перебрать все пары входных элементов можно за время O(n2).

Эффективность
(временная сложность)
O(n3) Кубический алгоритм часто содержит три вложенных цикла. Все тройки входных элементов можно перебрать за время O(n3).

Эффективность
(временная сложность)
O(2n) Такая временная сложность нередко указывает на то, что алгоритм перебирает все подмножества множества входных данных. Например, подмножествами множества {1, 2, 3} являются ∅, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3} и {1, 2, 3}.

Эффективность
(временная сложность)
O(n!) Такая временная сложность часто означает, что алгоритм перебирает все перестановки входных элементов. Например, перестановками множества
{1, 2, 3} являются (1, 2, 3), (1, 3, 2),
(2, 1, 3), (2, 3, 1), (3, 1, 2) и (3, 2, 1).

Эффективность
(временная сложность)
Алгоритм называется полиномиальным, если его временная сложность не выше O(nK), где k – константа. Все приведенные выше оценки временной сложности, кроме O(2n) и O(n!), полиномиальные. На практике константа k обычно мала, поэтому полиномиальная временная сложность, грубо говоря, означает, что алгоритм может обрабатывать большие входные данные.

Эффективность
(временная сложность)
Существует много важных задач, для которых полиномиальный алгоритм неизвестен, т. е. никто не знает, как решить их эффективно. Важным классом задач, для которых неизвестен полиномиальный алгоритм, являются NP-трудные задачи.

Эффективность
(временная сложность)
Вычислив временную сложность алгоритма, можно еще до его реализации проверить, будет ли он достаточно эффективен для решения задачи. Отправной точкой для оценки является тот факт, что современный компьютер может выполнить несколько сотен миллионов простых операций в секунду.

Эффективность
(временная сложность)
Например, предположим, что для задачи установлено временное ограничение – не более одной секунды – и что размер входных данных равен n = 105. Если временная сложность алгоритма равна O(n2), то он должен будет выполнить порядка (105)2 = 1010 операций. Это займет, по меньшей мере, несколько десятков секунд, поэтому такой алгоритм слишком медленный для решения задачи. Но если временная сложность равна O(n log n), то количество операций будет равно всего
105 log 105 ≈ 1.6 · 106, так что алгоритм гарантированно укладывается в отведенные рамки.

Эффективность
(временная сложность)
С другой стороны, зная размер входных данных, можно попытаться угадать временную сложность алгоритма, требуемую для решения задачи. В таблице приведены некоторые полезные оценки в предположении, что временное ограничение равно 1 секунде.

Эффективность
(временная сложность)
Например, если размер входных данных
n = 105, то, вероятно, можно ожидать, что временная сложность алгоритма равна O(n) или O(n log n). Обладание этой информацией упрощает проектирование алгоритма, поскольку сразу исключает подходы, приводящие к алгоритму с худшей временной сложностью.

Эффективность
(временная сложность)
Важно помнить, что временная
сложность – всего лишь оценка эффективности, поскольку она скрывает постоянные множители. Например, алгоритм с временной сложностью может выполнять как n/2, так и 5n операций, а это существенно влияет на фактическое время работы.

Эффективность
(временная сложность)
Что в действительности означают слова «время работы алгоритма составляет O(f (n))»? Что существуют такие константы c и n0, что алгоритм выполняет не более cf (n) операций при любых входных данных размера n ≥ n0. Таким образом, нотация O дает верхнюю границу времени работы алгоритма при достаточно объемных входных данных.

Эффективность
(временная сложность)
Например, технически правильно будет сказать, что временная сложность следующего алгоритма равна O(n2).
for (int i = 1; i <= n; i++) {
...
}
Однако оценка O(n) лучше, поэтому давать в этом случае оценку O(n2) – значит вводить в заблуждение читателя, т. к. любой человек предполагает, что нотация O служит для точной оценки временной сложности.

Эффективность
(временная сложность)
На практике часто применяются еще два варианта нотации. Буквой Ω обозначается нижняя граница времени работы алгоритма. Временная сложность алгоритма равна Ω(f (n)), если существуют константы c и n0 – такие, что алгоритм выполняет не менее cf (n) операций при любых входных данных размера n ≥ n0. Наконец, буквой Θ обозначается точная граница: временная сложность алгоритма равна Θ(f (n)), если она одновременно равна O(f (n)) и Ω(f (n)). Так, временная сложность приведенного выше алгоритма одновременно равна O(n) и Ω(n), поэтому она также равна Θ(n).

Эффективность
(временная сложность)
Описанная нотация используется во многих ситуациях, а не только в контексте временной сложности алгоритмов. Например, можно сказать, что массив содержит O(n) элементов или что алгоритм состоит из O(log n) раундов.

Эффективность
(пример)
Обсудим задачу, которую можно решить несколькими способами. Начнем с простого алгоритма с полным перебором, а затем предложим более эффективные решения, основанные на различных идеях.

Эффективность
(пример)
Пусть дан массив n чисел; задача заключается в том, чтобы вычислить максимальную сумму подмассивов, т. е. наибольшую возможную сумму последовательных элементов. Задача приобретает интерес, когда в массиве встречаются элементы с отрицательными значениями. На рисунке показан массив и его подмассив с максимальной суммой.

Эффективность
(пример)
Решение со сложностью O(n3). Задачу можно решить в лоб: перебрать все возможные подмассивы, вычислить сумму элементов в каждом подмассиве и запомнить максимальную сумму. Этот алгоритм реализован в следующем коде:
int best = 0;
for (int a = 0; a < n; a++) {
for (int b = a; b < n; b++) {
int sum = 0;
for (int k = a; k <= b; k++) {
sum += arr[k];
}
best = max(best, sum);
}
}
cout << best << "\n";
В переменных a и b хранятся первый и последний индекс подмассива, а в переменную sum записывается сумма его элементов. В переменной best хранится максимальная сумма, найденная в процессе просмотра. Временная сложность этого алгоритма равна O(n3), поскольку налицо три вложенных цикла, в которых перебираются входные данные.

Эффективность
(пример)
Решение со сложностью O(n2). Алгоритм легко сделать более эффективным, исключив один цикл. Для этого будем вычислять сумму одновременно со сдвигом правого конца подмассива. В результате получается такой код:
int best = 0;
for (int a = 0; a < n; a++) {
int sum = 0;
for (int b = a; b < n; b++) {
sum += arr[b];
best = max(best, sum);
}
}
cout << best << "\n";
После подобного изменения временная сложность становится равна O(n2).

Эффективность
(пример)
Решение со сложностью O(n). Оказывается, что задачу можно решить и за время O(n), т. е. достаточно и одного цикла. Идея в том, чтобы для каждой позиции массива вычислять максимальную сумму подмассива, заканчивающегося в этой позиции.
Рассмотрим подзадачу нахождения подмассива с максимальной суммой, заканчивающегося в позиции k. Есть две возможности:
Подмассив состоит из единственного элемента в позиции k.
Подмассив состоит из подмассива, заканчивающегося в позиции k − 1, за которым следует элемент в позиции k.
Во втором случае, поскольку ищется подмассив с максимальной суммой, сумма подмассива, заканчивающегося в позиции k – 1, также должна быть максимальной. Таким образом, задачу можно решить эффективно, если вычислять сумму максимального подмассива для каждой позиции последнего элемента слева направо.

Эффективность
(пример)
Алгоритм реализуется следующей программой:
int best = 0, sum = 0;
for (int k = 0; k < n; k++) {
sum = max(arr[k], sum + arr[k]);
best = max(best, sum);
}
cout << best << "\n";
В этом алгоритме только один цикл, в котором перебираются входные данные, поэтому его временная сложность равна O(n). Лучшей сложности добиться нельзя, поскольку любой алгоритм решения этой задачи должен хотя бы один раз проанализировать каждый элемент.

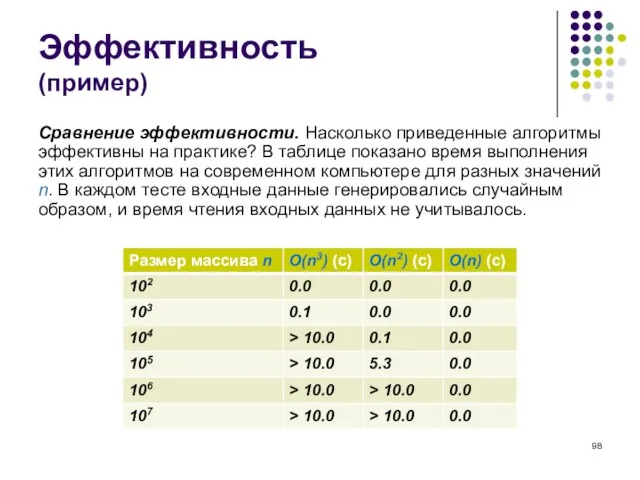
Эффективность
(пример)
Сравнение эффективности. Насколько приведенные алгоритмы эффективны на практике? В таблице показано время выполнения этих алгоритмов на современном компьютере для разных значений n. В каждом тесте входные данные генерировались случайным образом, и время чтения входных данных не учитывалось.

Эффективность
(пример)
Сравнение показывает, что все алгоритмы работают быстро, если размер входных данных мал, но по мере возрастания размера расхождение во времени становится очень заметным. Алгоритм со сложностью O(n3) замедляется, когда
n = 104, а алгоритм со сложностью
O(n2) – при n = 105. И лишь алгоритм со сложностью O(n) даже самые большие входные данные обрабатывает мгновенно.

Структуры данных
Познакомимся с наиболее важными структурами данных из стандартной библиотеки C++. В олимпиадном программировании чрезвычайно важно знать, какие структуры данных имеются в стандартной библиотеке и как ими пользоваться. Часто это позволяет сэкономить много времени при реализации алгоритма.

Структуры данных
В C++ обыкновенные массивы – это структуры фиксированного размера, т. е. после создания изменить размер уже нельзя.

Структуры данных
Динамическим называется массив, размер которого можно изменять в процессе выполнения программы. В стандартной библиотеке C++ имеется несколько динамических массивов, но полезнее всего вектор.

Структуры данных
(динамические массивы)
Вектор – это динамический массив, который позволяет эффективно добавлять элементы в конце и удалять последние элементы. Например, в следующем коде создается пустой вектор, в который затем добавляется три элемента:
vector
v;
v.push_back(3); // [3]
v.push_back(2); // [3, 2]
v.push_back(5); // [3, 2, 5]

Структуры данных
(динамические массивы)
Доступ к элементам осуществляется так же, как в обычном массиве:
cout << v[0] << "\n"; // 3
cout << v[1] << "\n"; // 2
cout << v[2] << "\n"; // 5

Структуры данных
(динамические массивы)
Еще один способ создать
вектор – перечислить все его элементы:
vector v = { 2, 4, 2, 5, 1 };

Структуры данных
(динамические массивы)
Можно также задать число элементов и их начальное значение:
vector
a(8); // размер 8, начальное значение 0
vector
b(8, 2); // размер 8, начальное значение 2

Структуры данных
(динамические массивы)
Функция size возвращает число элементов вектора. В следующем коде обходится вектор и печатаются его элементы:
for (int i = 0; i < v.size(); i++) {
cout << v[i] << "\n";
}

Структуры данных
(динамические массивы)
Обход вектора можно записать и короче:
for (auto x : v) {
cout << x << "\n";
}

Структуры данных
(динамические массивы)
Функция back возвращает последний элемент вектора, а функция pop_back удаляет последний элемент:
vector
v = { 2, 4, 2, 5, 1 };
cout << v.back() << "\n"; // 1
v.pop_back();
cout << v.back() << "\n"; // 5

Структуры данных
(динамические массивы)
Векторы реализованы так, что функции push_back и pop_back в среднем имеют сложность O(1). На практике работать с вектором почти так же быстро, как с массивом.

Структуры данных
(динамические массивы)
Итератором называется переменная, которая указывает на элемент структуры данных. Итератор begin указывает на первый элемент структуры, а итератор end – на позицию за последним элементом. Например, в случае вектора v, состоящего из восьми элементов, ситуация может выглядеть так:
[ 5, 2, 3, 1, 2, 5, 7, 1 ]
↑ ↑
v.begin() v.end()

Структуры данных
(динамические массивы)
Обратите внимание на асимметрию итераторов: begin() указывает на элемент, принадлежащий структуре данных, а end() ведет за пределы структуры данных.

Структуры данных
(динамические массивы)
Диапазоном называется последовательность соседних элементов структуры данных. Чаще всего диапазон задается с помощью двух итераторов: указывающего на первый элемент и на позицию за последним элементом. В частности, итераторы begin() и end() определяют диапазон, содержащий все элементы структуры данных.

Структуры данных
(динамические массивы)
Функции из стандартной библиотеки C++ обычно применяются к диапазонам. Так, в следующем фрагменте сначала вектор сортируется, затем порядок его элементов меняется на противоположный, и, наконец, элементы перемешиваются в случайном порядке.
sort(v.begin(), v.end());
reverse(v.begin(), v.end());
random_shuffle(v.begin(), v.end());

Структуры данных
(динамические массивы)
К элементу, на который указывает итератор, можно обратиться, воспользовавшись оператором *. В следующем коде печатается первый элемент вектора:
cout << *v.begin() << "\n";

Структуры данных
(динамические массивы)
Более полезный пример: функция lower_bound возвращает итератор на первый элемент отсортированного диапазона, значение которого не меньше x, а функция upper_bound – итератор на первый элемент, значение которого больше x:
vector
v = { 2, 3, 3, 5, 7, 8, 8, 8 };
auto a = lower_bound(v.begin(), v.end(), 5);
auto b = upper_bound(v.begin(), v.end(), 5);
cout << *a << " " << *b << "\n"; // 5 7

Структуры данных
(динамические массивы)
Отметим, что эти функции правильно работают, только если заданный диапазон отсортирован. В них применяется двоичный поиск, так что для поиска запрошенного элемента требуется логарифмическое время. Если искомый элемент не найден, то функция возвращает итератор на позицию, следующую за последним элементом диапазона.

Структуры данных
(динамические массивы)
В стандартной библиотеке C++ много полезных функций, заслуживающих внимания. Например, в следующем фрагменте создается вектор, содержащий уникальные элементы исходного вектора в отсортированном порядке:
sort(v.begin(), v.end());
v.erase(unique(v.begin(), v.end()), v.end());

Структуры данных
(динамические массивы)
Двусторонней очередью (деком) называется динамический массив, допускающий эффективные операции с обеих сторон. Как и вектор, двусторонняя очередь предоставляет функции push_back и pop_back, но вдобавок к ним функции push_front и pop_front. Используется она следующим образом:
deque
d;
d.push_back(5); // [5]
d.push_back(2); // [5, 2]
d.push_front(3); // [3, 5, 2]
d.pop_back(); // [3, 5]
d.pop_front(); // [5]

Структуры данных
(динамические массивы)
Операции двусторонней очереди в среднем имеют сложность O(1). Однако постоянные множители для них больше, чем для вектора, поэтому использовать двусторонние очереди имеет смысл, только когда требуется выполнять какие-то действия на обеих сторонах структуры.

Структуры данных
(динамические массивы)
C++ предоставляет также специализированные структуры данных, по умолчанию основанные на двусторонней очереди. Для стека определены функции push и pop, позволяющие вставлять и удалять элементы в конце структуры, а также функция top, возвращающая последний элемент без удаления:
stack
s;
s.push(2); // [2]
s.push(5); // [2, 5]
cout << s.top() << "\n"; // 5
s.pop(); // [2]
cout << s.top() << "\n"; // 2

Структуры данных
(динамические массивы)
В случае очереди элементы вставляются в начало, а удаляются из конца. Для доступа к первому и последнему элементам служат функции front и back.
queue
q;
q.push(2); // [2]
q.push(5); // [2, 5]
cout << q.front() << "\n"; // 2
q.pop(); // [5]
cout << q.back() << "\n"; // 5

Структуры данных
(множества)
Множеством называется структура данных, в которой хранится набор элементов. Основные операции над множествами – вставка, поиск и удаление. Множества реализованы так, что все эти операции эффективны, что часто позволяет улучшить время работы алгоритмов, в которых множества используются.

Структуры данных
(множества)
В стандартной библиотеке C++ имеются две структуры, относящиеся к множествам:
set основана на сбалансированном двоичном дереве поиска, его операции работают за время O(log n);
unordered_set основана на хеш-таблице и работает в среднем O(1).

Структуры данных
(множества)
Обе структуры эффективны, и во многих случаях годится любая. Поскольку используются они одинаково, в примерах ограничимся только структурой set.

Структуры данных
(множества)
В показанном ниже коде создается множество, содержащее целые числа, и демонстрируются некоторые его операции. Функция insert добавляет элемент во множество, функция count возвращает количество вхождений элемента во множество, а функция erase удаляет элемент из множества.
set
s;
s.insert(3);
s.insert(2);
s.insert(5);
cout << s.count(3) << "\n"; // 1
cout << s.count(4) << "\n"; // 0
s.erase(3);
s.insert(4);
cout << s.count(3) << "\n"; // 0
cout << s.count(4) << "\n"; // 1

Структуры данных
(множества)
Важным свойством множеств является тот факт, что все их элементы различны. Следовательно, функция count всегда возвращает 0 (если элемент не принадлежит множеству) или 1 (если принадлежит), а функция insert никогда не добавляет элемент во множество, если он в нем уже присутствует. Это демонстрируется в следующем фрагменте:
set
s;
s.insert(3);
s.insert(3);
s.insert(3);
cout << s.count(3) << "\n"; // 1

Структуры данных
(множества)
Множество в основном можно использовать как вектор, однако доступ к элементам с помощью оператора [] невозможен. В следующем коде печатается количество элементов во множестве, а затем эти элементы перебираются:
cout << s.size() << "\n";
for (auto x : s) {
cout << x << "\n";
}

Структуры данных
(множества)
Функция find(x) возвращает итератор, указывающий на элемент со значением x. Если же множество не содержит x, то возвращается итератор end().
auto it = s.find(x);
if (it == s.end()) {
// x не найден
}

Структуры данных
(множества)
Упорядоченные множества. Основное различие между двумя структурами множества в C++ – то, что set упорядочено, а unordered_set не упорядочено. Поэтому если порядок элементов важен, то следует пользоваться структурой set.

Структуры данных
(множества)
Рассмотрим задачу о нахождении наименьшего и наибольшего значений во множестве. Чтобы сделать это эффективно, необходимо использовать структуру set. Поскольку элементы отсортированы, найти наименьшее и наибольшее значения можно следующим образом:
auto first = s.begin();
auto last = s.end(); last--;
cout << *first << " " << *last << "\n";
Поскольку end() указывает на позицию, следующую за последним элементом, то необходимо уменьшить итератор на единицу.

Структуры данных
(множества)
В структуре set имеются также функции lower_bound(x) и upper_bound(x), которые возвращают итератор на наименьший элемент множества, значение которого не меньше x или больше x соответственно. Если искомого элемента не существует, то обе функции возвращают end().
cout << *s.lower_bound(x) << "\n";
cout << *s.upper_bound(x) << "\n";

Структуры данных
(множества)
Мультимножества. В отличие от множества, в мультимножество один и тот же элемент может входить несколько раз. В C++ имеются структуры multiset и unordered_multiset, похожие на set и unordered_set. В следующем коде в мультимножество три раза добавляется значение 5.
multiset
s;
s.insert(5);
s.insert(5);
s.insert(5);
cout << s.count(5) << "\n"; // 3

Структуры данных
(множества)
Функция erase удаляет все копии значения из мультимножества.
s.erase(5);
cout << s.count(5) << "\n"; // 0

Структуры данных
(множества)
Если требуется удалить только одно значение, то можно поступить так:
s.erase(s.find(5));
cout << s.count(5) << "\n"; // 2

Структуры данных
(множества)
Отметим, что во временной сложности функций count и erase имеется дополнительный множитель O(k), где
k – количество подсчитываемых (удаляемых) элементов. В частности, подсчитывать количество копий значения в мультимножестве с помощью функции count неэффективно.

Структуры данных
(множества)
Отображением называется множество, состоящее из пар ключ-значение. Отображение можно также рассматривать как обобщение массива. Если в обыкновенном массиве ключами служат последовательные целые числа
0, 1, …, n − 1, где n – размер массива, то в отображении ключи могут иметь любой тип и необязательно должны быть последовательными.

Структуры данных
(множества)
В стандартной библиотеке C++ есть две структуры отображений, соответствующие структурам множеств: в основе map лежит сбалансированное двоичное дерево со временем доступа к элементам O(log n), а в основе unordered_map – техника хеширования со средним временем доступа к элементам O(1).

Структуры данных
(множества)
В следующем фрагменте создается отображение, ключами которого являются строки, а значениями – целые числа:
map
m;
m["monkey"] = 4;
m["banana"] = 3;
m["harpsichord"] = 9;
cout << m["banana"] << "\n"; // 3

Структуры данных
(множества)
Если в отображении нет запрошенного ключа, то он автоматически добавляется, и ему сопоставляется значение по умолчанию. Например, в следующем коде в отображение добавляется ключ «aybabtu» со значением 0.
map
m;
cout << m["aybabtu"] << "\n"; // 0

Структуры данных
(множества)
Функция count проверяет, существует ли ключ в отображении:
if (m.count("aybabtu")) {
// ключ существует
}

Структуры данных
(множества)
В следующем коде печатаются все имеющиеся в отображении ключи и значения:
for (auto x : m) {
cout << x.first << " " << x.second << "\n";
}

Структуры данных
(эксперименты)
Хотя временная сложность – отличный инструмент, она не всегда сообщает всю правду об эффективности, поэтому имеет смысл провести эксперименты с настоящими реализациями и наборами данных.

Структуры данных
(эксперименты)
Многие задачи можно решить, применяя как множества, так и сортировку. Важно понимать, что алгоритмы на основе сортировки обычно гораздо быстрее, даже если это не очевидно из одного лишь анализа временной сложности.

Структуры данных
(эксперименты)
В качестве примера рассмотрим задачу о вычислении количества уникальных элементов вектора. Одно из возможных
решений – поместить все элементы во множество и вернуть размер этого множества. Поскольку порядок элементов не важен, можно использовать как set, так и unordered_set. Можно решить задачу и по-другому: сначала отсортировать вектор, а затем обойти его элементы. Подсчитать количество уникальных элементов отсортированного вектора просто.

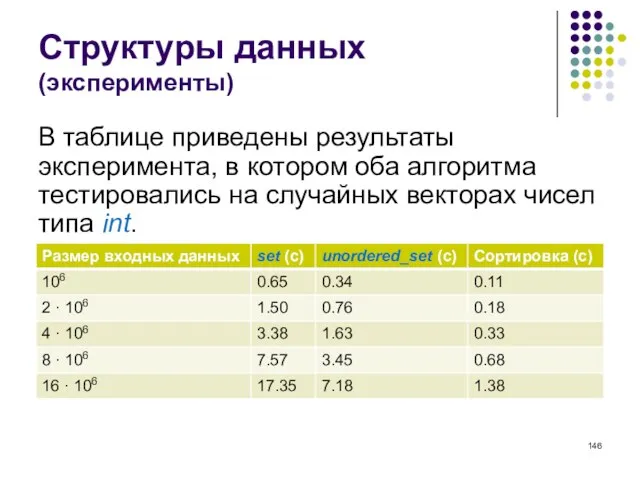
Структуры данных
(эксперименты)
В таблице приведены результаты эксперимента, в котором оба алгоритма тестировались на случайных векторах чисел типа int.

Структуры данных
(эксперименты)
Оказалось, что алгоритм на основе unordered_set примерно в два раза быстрее алгоритма на основе set, а алгоритм на основе сортировки быстрее алгоритма на основе set более чем в 10 раз. Отметим, что временная сложность обоих алгоритмов равна O(n log n), и тем не менее алгоритм на основе сортировки работает гораздо быстрее. Причина в том, что сортировка – простая операция, тогда как сбалансированное двоичное дерево поиска, применяемое в реализации set, – сложная структура данных.

Структуры данных
(эксперименты)
Отображения – удобные структуры данных, по сравнению с массивами, поскольку позволяют использовать индексы любого типа, но и постоянные множители велики. В следующем эксперименте мы создали вектор, содержащий n случайных целых чисел от 1 до 106, а затем искали самое часто встречающееся значение путем подсчета числа вхождений каждого элемента. Сначала мы использовали отображения, но поскольку число 106 достаточно мало, то можно использовать и массивы.

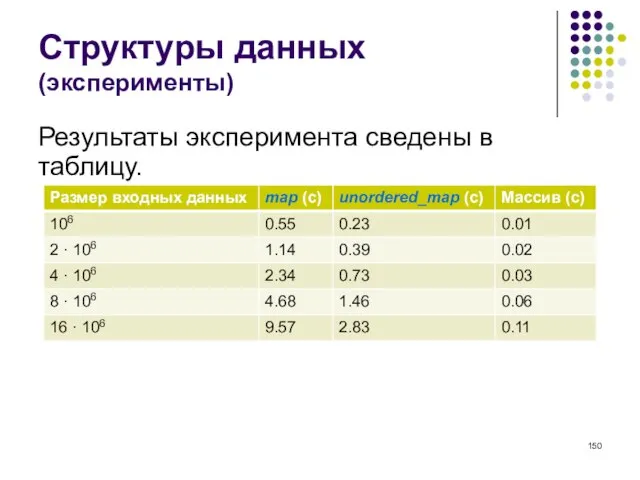
Структуры данных
(эксперименты)
Результаты эксперимента сведены в таблицу. Хотя unordered_map примерно в три раза быстрее map, массив все равно почти в 100 раз быстрее. Таким образом, по возможности следует пользоваться массивами, а не отображениями. Особо отметим, что хотя временная сложность операций unordered_map равна O(1), скрытые постоянные множители, характерные для этой структуры данных, довольно велики.

Структуры данных
(эксперименты)
Результаты эксперимента сведены в таблицу.

Структуры данных
(эксперименты)
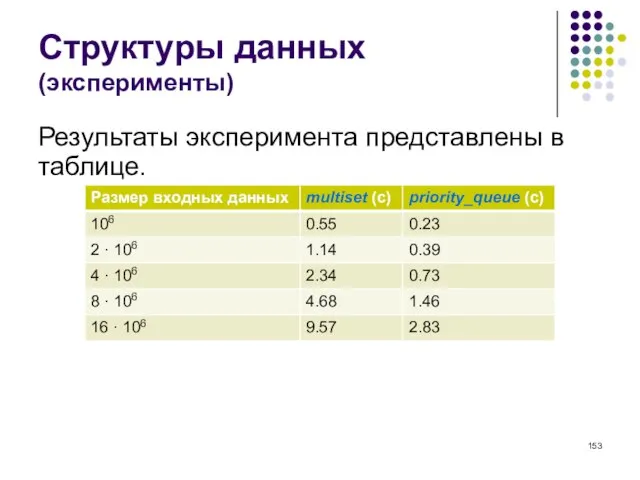
Хотя unordered_map примерно в три раза быстрее map, массив все равно почти в 100 раз быстрее. Таким образом, по возможности следует пользоваться массивами, а не отображениями. Хотя временная сложность операций unordered_map равна O(1), скрытые постоянные множители, характерные для этой структуры данных, довольно велики.

Структуры данных
(эксперименты)
Верно ли, что очереди с приоритетом действительно быстрее мультимножеств? Чтобы выяснить это, проведем еще один эксперимент. Создадим два вектора, содержащие n случайных чисел типа int. Сначала добавим все элементы первого вектора в структуру данных, а затем обойдем второй вектор и на каждом шаге удалим наименьший элемент из структуры данных и добавим в нее новый элемент.

Структуры данных
(эксперименты)
Результаты эксперимента представлены в таблице.