Содержание
- 2. Правило переведення числа з двійкової системи числення у вісімкову Щоб перевести число із двійкової системи у
- 3. Приклад Число 1001011 2 Цифр у числі 7, недостатньо, щоб розбити на три тріади. Щоб було
- 4. Правило переведення числа з двійкової системи числення у шістнадцяткову Щоб перевести число з двійкової системи до
- 5. Число 1011100011 2 Цифр у числі 10, недостатньо, щоб розбити на три тетради. Щоб було достатньо,
- 6. Правило переведення числа з двійкової системи числення у десяткову Для переведення двійкового числа до десяткового необхідно
- 7. Приклад n (степінь) 2 n Cтепені числа 2
- 8. Правило переведення числа з вісімкової системи числення у десяткову Для переведення вісімкового числа до десяткового необхідно
- 9. Приклад n (степінь) 8 n Степені числа 8
- 10. Правило переведення числа з вісімкової системи числення у двійкову Для переведення вісімкового числа до двійкового необхідно
- 11. Приклад 531 8 = 101011001 2
- 12. Правило переведення числа з вісімкової системи числення у шістнадцяткову При переході з вісімкової системи числення в
- 13. Приклад Двійкова Вісімкова
- 14. Правило переведення числа з десяткової системи числення у двійкову Для переведення десяткового числа в двійкову систему
- 15. Приклад Число 22 10. Алгоритм: Відповідь:
- 16. Правило переведення числа з десяткової системи числення у вісімкову Для переведення десяткового числа в вісімкову систему
- 17. Приклад Число 571 10. Алгоритм: Відповідь:
- 18. Правило переведення числа з десяткової системи числення у шістнадцяткову Для переведення десяткового числа в шістнадцяткову систему
- 19. Приклад Число 7476 10. Алгоритм: Відповідь:
- 21. Скачать презентацию


















 Повторение и закрепление изученного. Урок информатики в 4 классе
Повторение и закрепление изученного. Урок информатики в 4 классе Программирование в среде Robot C. Занятие 3
Программирование в среде Robot C. Занятие 3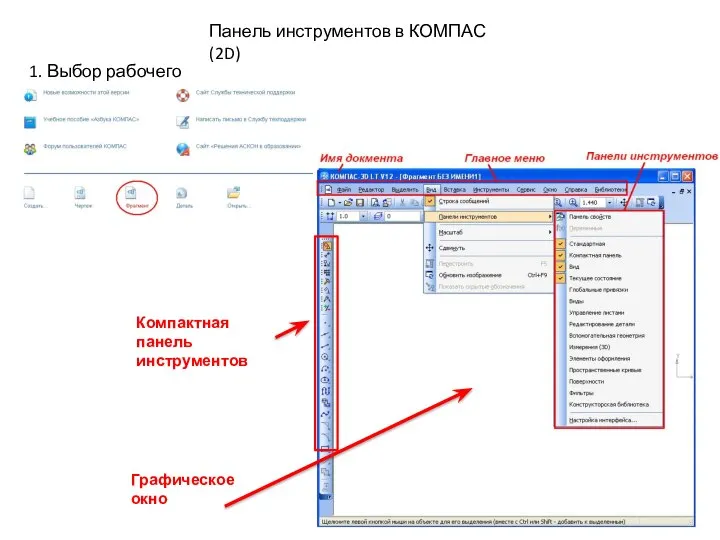 Панель инструментов в Компас-(2D). Практика 1
Панель инструментов в Компас-(2D). Практика 1 7-2-1
7-2-1 Текстовая информация. Единицы измерения
Текстовая информация. Единицы измерения Анимация. 3D графика
Анимация. 3D графика Персональные компьютеры и приложения
Персональные компьютеры и приложения Профессия моего папы инженер-программист
Профессия моего папы инженер-программист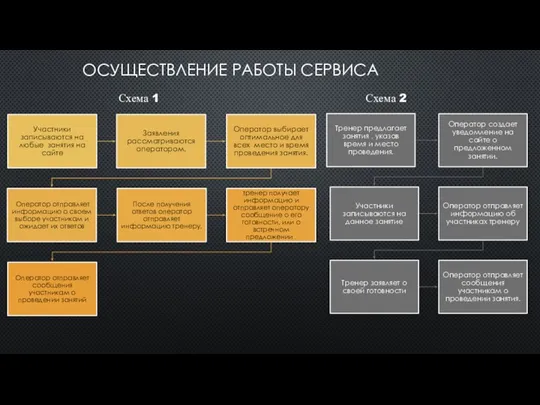 Осуществление работы сервиса
Осуществление работы сервиса Создание архива данных. Извлечение данных из архива
Создание архива данных. Извлечение данных из архива Табличные информационные модели. Моделирование и формализация
Табличные информационные модели. Моделирование и формализация Понятие информации
Понятие информации Программное обеспечение компьютера
Программное обеспечение компьютера Упаковка и распаковка данных с помощью программ-архиваторов. WinRAR
Упаковка и распаковка данных с помощью программ-архиваторов. WinRAR Настольные издательские системы
Настольные издательские системы 3D – печать. Механизмы и кинематика
3D – печать. Механизмы и кинематика Основы работы в Excel (урок 1)
Основы работы в Excel (урок 1) Спасибо, Дед Мороз!
Спасибо, Дед Мороз! Отношения между объектами
Отношения между объектами Информатика. Занятие 5
Информатика. Занятие 5 Принципы работы в соцсетях. Проектная деятельность
Принципы работы в соцсетях. Проектная деятельность Виды информации (интерактивный тест, 8 класс)
Виды информации (интерактивный тест, 8 класс) Порт PS/2
Порт PS/2 Information Technologies. Работа в области тестирования, разработки и продвижения интернет ресурсов
Information Technologies. Работа в области тестирования, разработки и продвижения интернет ресурсов Партнерская Система ЗОРАН как система искусственного интеллекта (часть первая: практическая значимость)
Партнерская Система ЗОРАН как система искусственного интеллекта (часть первая: практическая значимость) Отношение объектов и их множеств. Отношения между множествами. Отношение входитв состав
Отношение объектов и их множеств. Отношения между множествами. Отношение входитв состав Начало информационной эпохи. Постмодернизм
Начало информационной эпохи. Постмодернизм Открытый урок 29.09.2022 ОП.13 ССА 2.2 (1)
Открытый урок 29.09.2022 ОП.13 ССА 2.2 (1)