Содержание
- 2. Схемы программ Программа – способ задания алгоритма. Свойства программ: является конструктивным объектом; работает конечное время; характерны
- 3. Схемы программ – математические модели программ. Свойства схем программ: позволяют изучать свойства широких классов программ; сохраняют
- 4. Стандартные схемы программ Класс стандартных схем включает: константы; простые переменные; выражения; операторы присваивания; условные операторы; метки;
- 5. Базис В класса стандартных схем состоит: 4 счетных множества символов; множество операторов. Множества символов: Переменные: Х={х1,
- 6. Множество операторов: 1) начальный оператор: старт(х1, х2...хk); 2) заключительный оператор: стоп (t1, t2...tn); 3) оператор присваивания:
- 7. Программа: void main(void) { int x, y; cin>>x; y=1; while (x>0) { y=x*y; x--; } cout
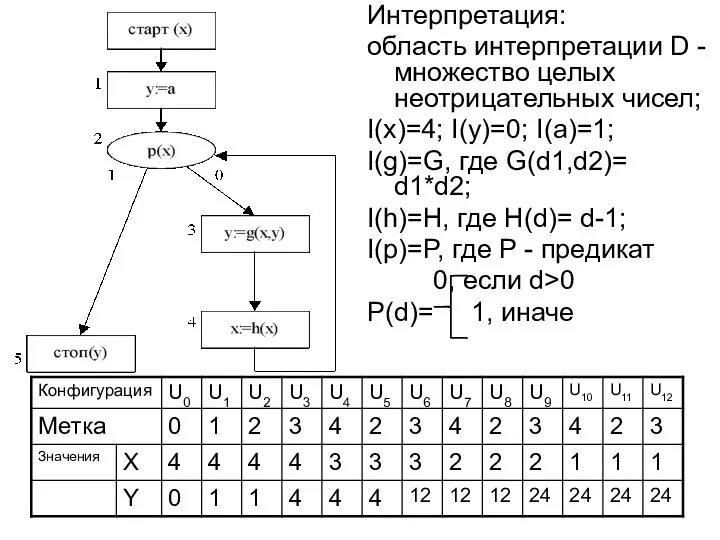
- 8. Интерпретация: область интерпретации D - множество целых неотрицательных чисел; I(x)=4; I(y)=0; I(a)=1; I(g)=G, где G(d1,d2)= d1*d2;
- 9. Рекурсивные схемы FACT(x), FACT(x)=если х=0 то 1 иначе x*FACT(x-1). FACT(4)=если 4=0 то 1 иначе 4*FACT(4-1)= =4*FACT(3)=4*(если
- 10. Базис РС включает: 4 счетных множества символов: Переменные; Функциональные символы; Предикатные символы; Специальные символы. Множество логических
- 11. Термы: 1. Простые термы Базовые термы; Вызовы (F(n)(t1, t2, …, tn)). 2. Условные термы: если π
- 12. Рекурсивное уравнение: F(n)(x1, x2, …, xn)=t(x1, x2, …, xn) Рекурсивная схема: (t, M) Рекурсивная программа: (RS,
- 13. Протокол выполнения рекурсивной программы RS1: F(x), F(x)=если p(x) то a иначе g(x, F(h(x))). I(x)=4; I(a)=1; I(g)=G,
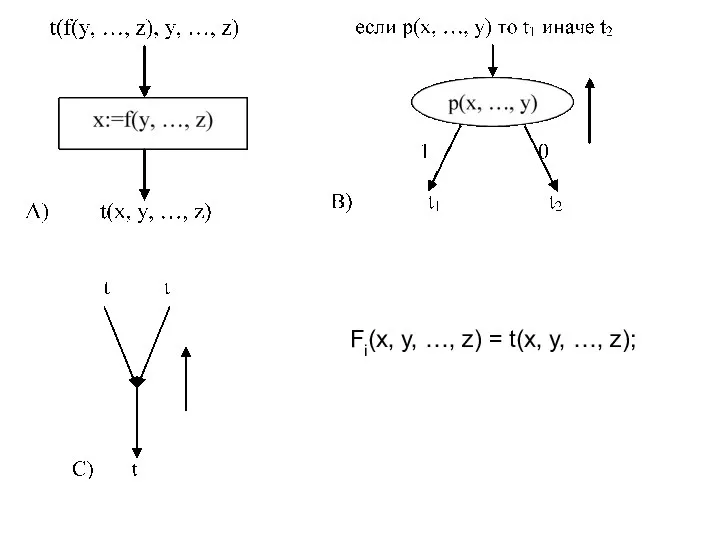
- 14. Трансляция схем программ Теорема Маккарти: Класс стандартных схем транслируем в класс рекурсивных схем. Алгоритм трансляции: Точки
- 15. Fi(x, y, …, z) = t(x, y, …, z);
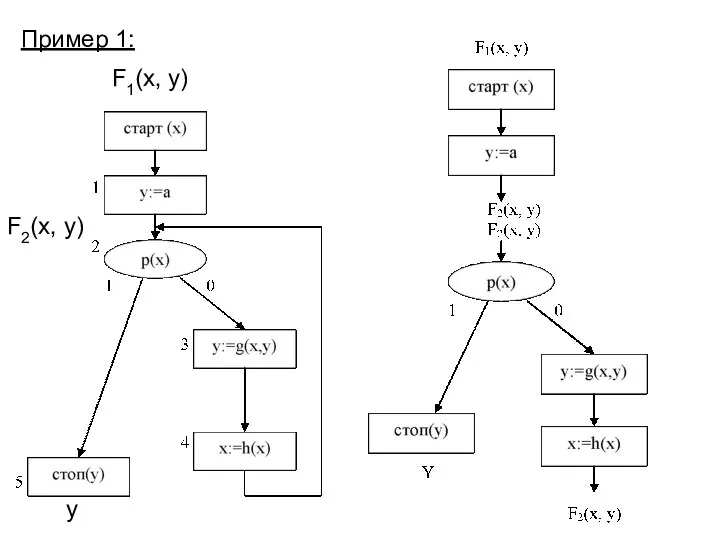
- 16. Пример 1: F1(x, y) F2(x, y) y
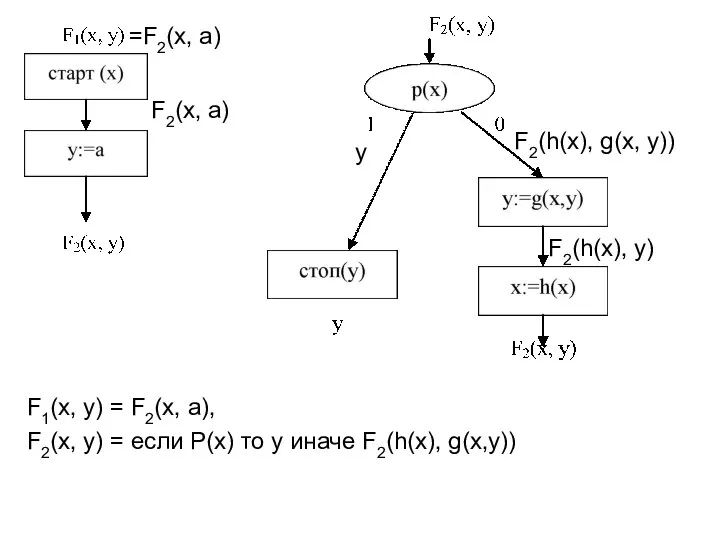
- 17. F2(x, a) =F2(x, a) y F2(h(x), y) F2(h(x), g(x, y)) F1(x, y) = F2(x, a), F2(x,
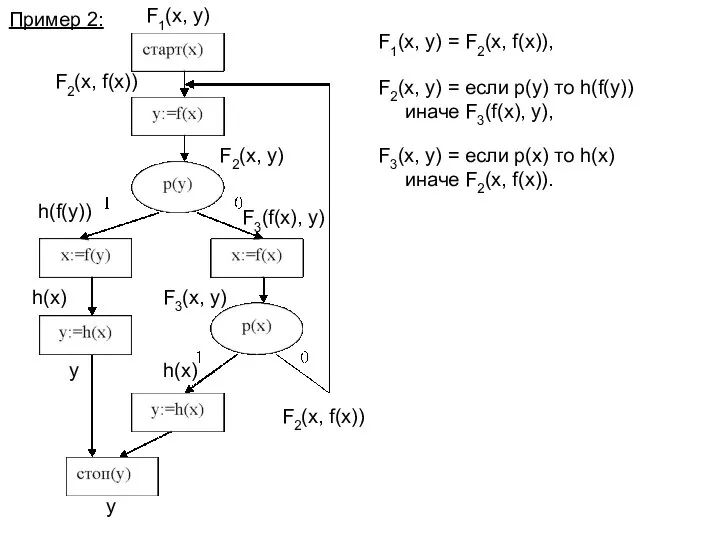
- 18. Пример 2: F1(x, y) F2(x, y) F3(x, y) y F2(x, f(x)) F1(x, y) = F2(x, f(x)),
- 19. Линейные унарные рекурсивные схемы F(x), F(x) = если p(x) то f(x) иначе F(F(g(x))). F(a), F(x) =
- 20. Схемы с процедурами Главная схема x=F(n)(y1, y2, …, yn) Множество схем процедур.
- 21. Трансляция рекурсивных схем в схемы с процедурами (старт (y1, y2, …, yn), 1: y:=t (y1, y2,
- 22. Рекурсивная схема: S: F(x), F(x)=если p(x) то x иначе f(F(g(x)), F(h(x))) Схема с процедурами:
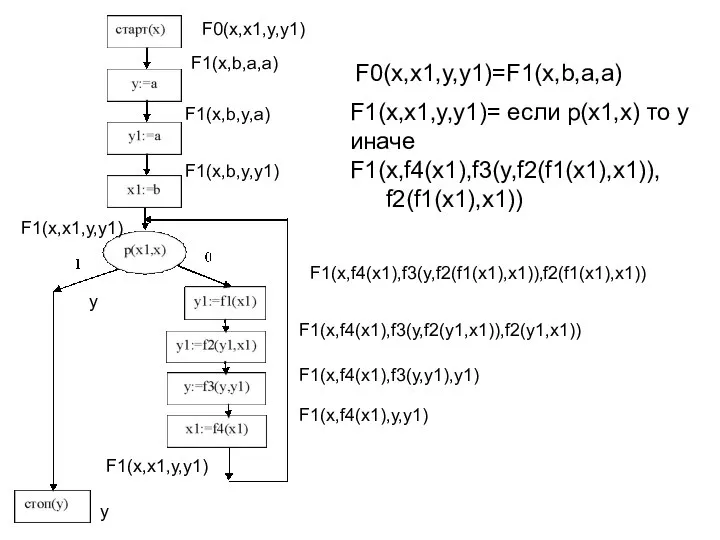
- 23. F0(x,x1,y,y1) F1(x,x1,y,y1) y F1(x,b,y,y1) F1(x,b,y,a) F1(x,b,a,a) F0(x,x1,y,y1)=F1(x,b,a,a) y F1(x,x1,y,y1) F1(x,f4(x1),y,y1) F1(x,f4(x1),f3(y,y1),y1) F1(x,f4(x1),f3(y,f2(y1,x1)),f2(y1,x1)) F1(x,f4(x1),f3(y,f2(f1(x1),x1)),f2(f1(x1),x1)) F1(x,x1,y,y1)= если p(x1,x)
- 24. F0(x,x1,y,y1)=F1(x,b,a,a) F1(x,x1,y,y1)= если p(x1,x) то y иначе F1(x,f4(x1),f3(y,f2(f1(x1),x1)),f2(f1(x1),x1)) S: (старт (x), 1: x1:=b; 2: y:=a; 3:
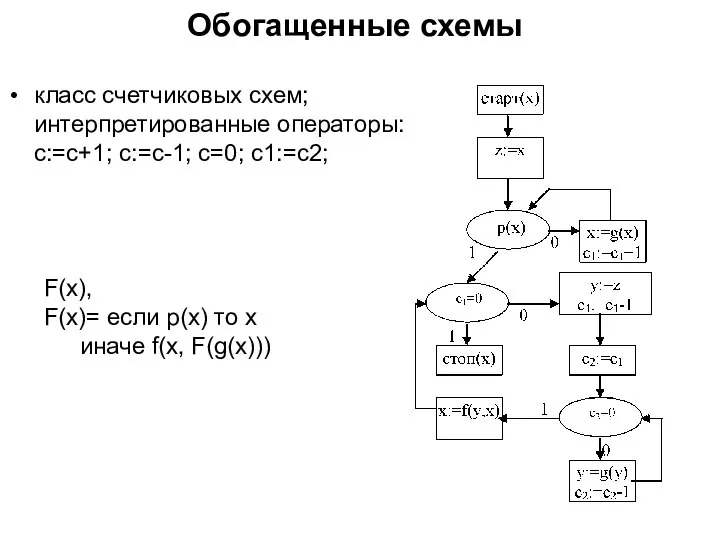
- 25. Обогащенные схемы класс счетчиковых схем; интерпретированные операторы: c:=c+1; c:=c-1; c=0; c1:=c2; F(x), F(x)= если р(х) то
- 26. класс магазинных схем; интерпретированные операторы: M:=x; x:=M; M=Ø; класс схем с массивами; интерпретированные операторы: A[c]:=x; x:=A[c].
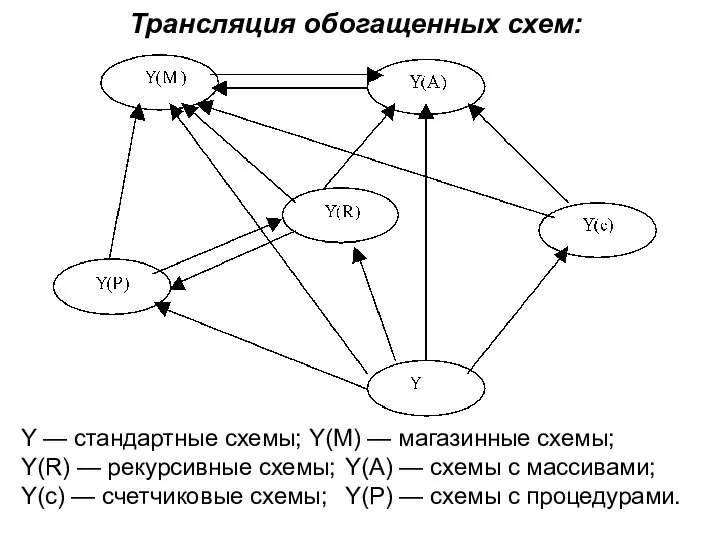
- 27. Трансляция обогащенных схем: Y — стандартные схемы; Y(М) — магазинные схемы; Y(R) — рекурсивные схемы; Y(А)
- 28. Структурированные схемы (о0, о1, …, оn) Специальные символы: если, то, иначе, пока, цикл, конец. Три типа
- 30. Скачать презентацию

















![класс магазинных схем; интерпретированные операторы: M:=x; x:=M; M=Ø; класс схем с массивами; интерпретированные операторы: A[c]:=x; x:=A[c].](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/955491/slide-25.jpg)

 Многоуровневые справочники. Практическая работа /блок №2
Многоуровневые справочники. Практическая работа /блок №2 Интернет-ресурсы. Подготовка к ЕГЭ по математике
Интернет-ресурсы. Подготовка к ЕГЭ по математике MalakhovOFF advertises LIVE: his well-baby check
MalakhovOFF advertises LIVE: his well-baby check Разработка автоматизированной информационной системы для руководителей объединений в Центре детского творчества
Разработка автоматизированной информационной системы для руководителей объединений в Центре детского творчества Модификатор Зеркало и создание разрезов
Модификатор Зеркало и создание разрезов Условный оператор в языке программирования Pascal
Условный оператор в языке программирования Pascal Стандарты технологии Ethernet, TokenRing, FDD
Стандарты технологии Ethernet, TokenRing, FDD Магазин БАДов
Магазин БАДов Понятие об электронной таблице
Понятие об электронной таблице Мой личный сайт. Проект
Мой личный сайт. Проект Лицензионные и свободно распространяемые программные продукты
Лицензионные и свободно распространяемые программные продукты Крауд маркетинг
Крауд маркетинг Дискретное представление информации
Дискретное представление информации HTML. Разработка Web-сайта
HTML. Разработка Web-сайта Раунд длиною в жизнь
Раунд длиною в жизнь Система дистанционного обучения Moodle
Система дистанционного обучения Moodle Репутация объекта Центр сертификации в период апрель 2019
Репутация объекта Центр сертификации в период апрель 2019 Способы записи алгоритмов. Основы алгоритмизации
Способы записи алгоритмов. Основы алгоритмизации Текст и его типы
Текст и его типы Социальные сети: Студенты. Терроризм
Социальные сети: Студенты. Терроризм Okna_i_operatsii_nad_oknami
Okna_i_operatsii_nad_oknami Режимы и способы обработки данных
Режимы и способы обработки данных Задачи и решения для модуля: цикл for
Задачи и решения для модуля: цикл for Информационные системы
Информационные системы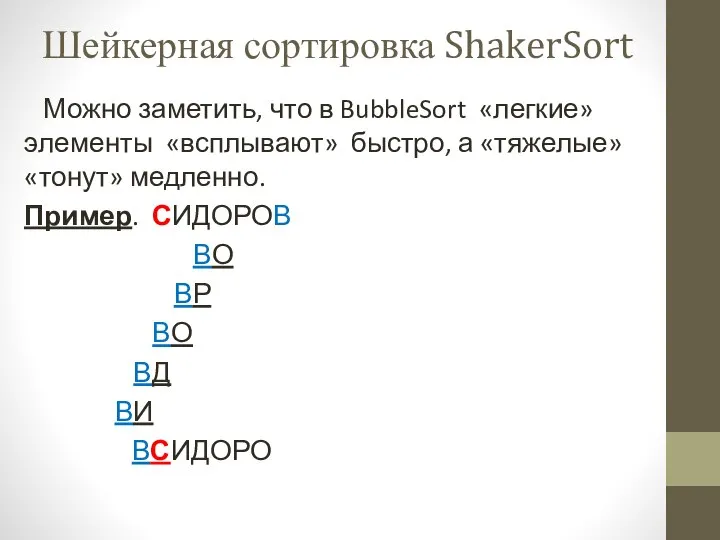 Шейкерная сортировка ShakerSort
Шейкерная сортировка ShakerSort Виртуальная экскурсия по мастерским WorldSkills
Виртуальная экскурсия по мастерским WorldSkills Устройства хранения данных. Файлы и папки. Работа с файловым менеджером и программами-утилитами операционной системы
Устройства хранения данных. Файлы и папки. Работа с файловым менеджером и программами-утилитами операционной системы Кодирование информации. 5 класс
Кодирование информации. 5 класс