Восьмеричная и шестнадцатеричные системы счисления. Компьютерные системы счисления. Правило перевода целых десятичных чисел

Цели урока:
образовательные – выяснить, почему именно двоичная система счисления используется в компьютере, показать связь между двоичной, восьмеричной и шестнадцатеричной системами счисления; сформировать знания и умения перевода небольших десятичных и двоичных чисел в восьмеричную и шестнадцатеричную системы счисления.
развивающие – умение анализировать любую позиционную систему счисления как знаковую систему;
воспитательные – понимание роли фундаментальных знаний как основы современных информационных технологий.

Задачи:
1) рассмотрение восьмеричной системы счисления как знаковой системы;
2) рассмотрение правила перевода целых десятичных чисел в восьмеричную систему счисления
3) рассмотрение шестнадцатеричной системы счисления как знаковой системы;
4) рассмотрение правила перевода целых десятичных чисел в шестнадцатеричную систему счисления;
5) рассмотрение правила перевода двоичных чисел в шестнадцатеричную и восьмеричную системы счисления;
6) характеристика двоичной, восьмеричной и шестнадцатеричной систем счисления с точки зрения их использования в компьютерной технике.

an–1an–2…a1a0 = an–1×8n–1+an–2×8n–2+…+a0×80
Пример: 10638 =1×83 +0×82+6×81+3×80=56310.
Для перевода целого восьмеричного числа в десятичную систему счисления следует перейти к его развёрнутой записи и вычислить значение получившегося выражения.
Восьмеричная система счисления
Для перевода целого десятичного числа в восьмеричную систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на 8 до тех пор, пока не получим частное, равное нулю.
Восьмеричной системой счисления называется позиционная система счисления с основанием 8.
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7.

Основание: q = 16.
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
Шестнадцатеричная система счисления
Переведём десятичное число 154 в шестнадцатеричную систему счисления:
15410 = 9А16
154
16
9
-144
10
(А)
9
16
0
3АF16 =3×162+10×161+15×160 =768+160+15=94310.

1) последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получим частное, равное нулю;
2) полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления;
3) составить число в новой системе счисления, записывая его, начиная с последнего полученного остатка.
Цифровые весы
Правило перевода целых десятичных чисел в систему счисления с основанием q

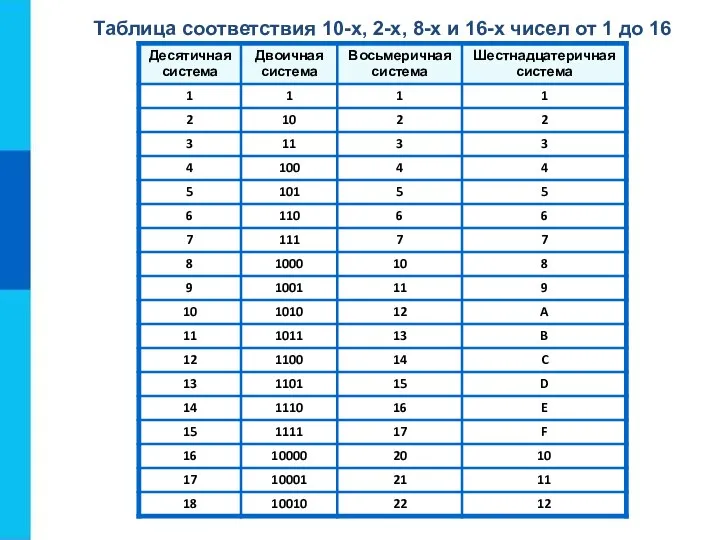
Таблица соответствия 10-х, 2-х, 8-х и 16-х чисел от 1 до 16

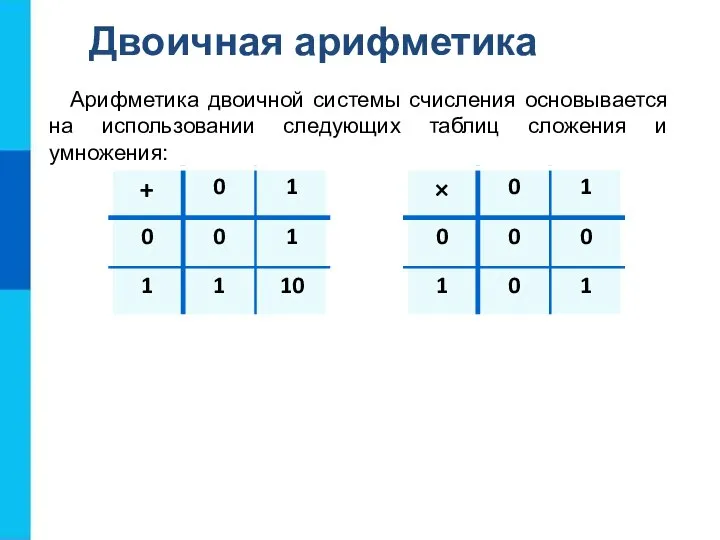
Двоичная арифметика
Арифметика двоичной системы счисления основывается на использовании следующих таблиц сложения и умножения: