Содержание
- 2. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ.
- 3. Статистика — это точная наука, изучающая методы сбора, анализа и обработки данных, которые описывают массовые действия,
- 4. СТАТИСТИКА ИЗУЧАЕТ: численность отдельных групп населения страны и ее регионов; производство и потребление разнообразных видов продукции;
- 5. ОПРЕДЕЛЕНИЕ: Ряд данных – это ряд результатов каких-либо измерений. Например: 1 ) измерения роста человека 2)
- 6. Объемом ряда данных называется количество всех данных. Например: дан ряд чисел 1; 3; 6; -4; 0
- 10. Модой ряда данных называется число ряда, которое встречается в этом ряду наиболее часто. Медиана с нечётным
- 11. Полигон распределения – это зависимость абсолютной частоты варианта mi от значения варианта i x . Эту
- 12. Рассмотрим простейшую задачу данного типа. Задача: Измерение роста детей младшей группы детского сада представлено выборкой: 92,
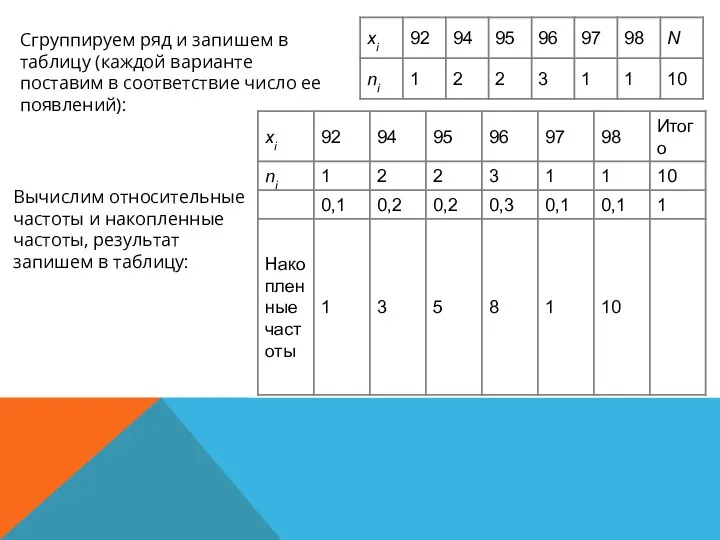
- 13. Вычислим относительные частоты и накопленные частоты, результат запишем в таблицу: Сгруппируем ряд и запишем в таблицу
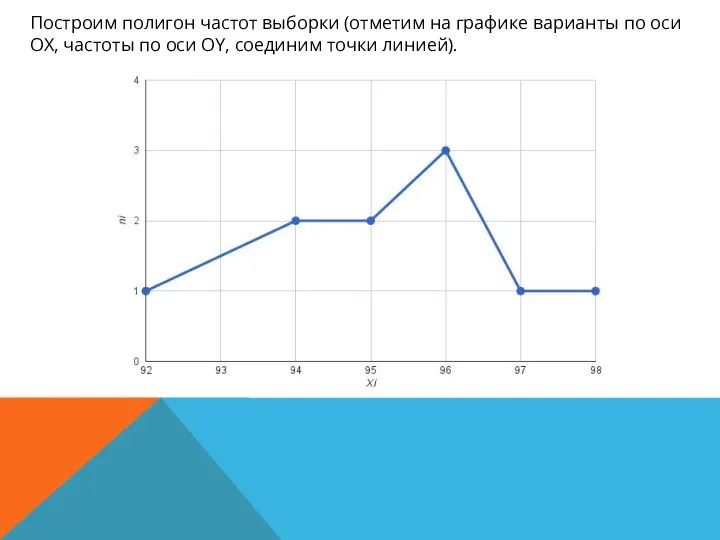
- 14. Построим полигон частот выборки (отметим на графике варианты по оси ОХ, частоты по оси OY, соединим
- 15. Математическое ожидание - случайной величины XX (обозначается M(X)M(X) или реже E(X)E(X)) характеризует среднее значение случайной величины
- 16. Пример 1. Вычислить математическое ожидание дискретной случайной величины Х, заданной рядом: Xi −1 2 5 10
- 17. Математическое ожидание дискретной случайной величины. Говоря простым языком, это среднеожидаемое значение при многократном повторении испытаний. Пусть
- 18. Пример: Мистер Х играет в европейскую рулетку по следующей системе: постоянно ставит 100 рублей на «красное».
- 19. Вычислим, например, математическое ожидание случайной величины – количества выпавших на игральном кубике очков: очка В чём
- 20. Теперь вспомним нашу гипотетическую игру: Возникает вопрос: а выгодно ли вообще играть в эту игру? …у
- 21. Упорядоченными рядами данных называются ряды, в которых данные расположены по какому то правилу. Как упорядочить ряд
- 22. Таблица распределения данных – это таблица упорядоченного ряда, в котором вместо повторений одного и того же
- 23. Номинативный ряд данных – это НЕ ЧИСЛОВЫЕ ДАННЫЕ, а например, имена; названия; номинации… Например: список финалистов
- 24. Вероятность случайного события равна дроби, в знаменателе которой содержится число всех равновероятных возможностей, из которых состоит
- 25. Группировка данных – применяется когда различных результатов измерений слишком много. Т.е их объединяют в группы. При
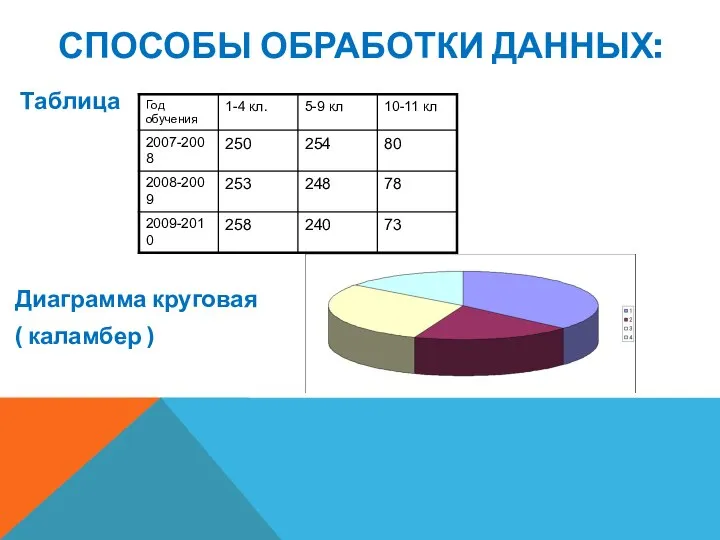
- 26. СПОСОБЫ ОБРАБОТКИ ДАННЫХ: Таблица Диаграмма круговая ( каламбер )
- 28. Скачать презентацию






















 Мішані числа
Мішані числа Подготовка к дифференцированному зачёту по математике. Нижегородский авиационный технический колледж
Подготовка к дифференцированному зачёту по математике. Нижегородский авиационный технический колледж Начертательная геометрия
Начертательная геометрия Параллельные прямые
Параллельные прямые Презентация на тему ГИА 2013. Модуль Геометрия №10
Презентация на тему ГИА 2013. Модуль Геометрия №10  Решение квадратных неравенств
Решение квадратных неравенств Применение определенного интеграла при решении геометрических и физических задач
Применение определенного интеграла при решении геометрических и физических задач Больше, меньше, столько же
Больше, меньше, столько же История появления тригонометрии
История появления тригонометрии Математическая карусель
Математическая карусель Решение систем неравенств с одной переменной
Решение систем неравенств с одной переменной Графики уравнений
Графики уравнений А-11 Триг функции и их свойства 29.09.22 - копия
А-11 Триг функции и их свойства 29.09.22 - копия Преобразование графиков функций
Преобразование графиков функций Целое и части
Целое и части Отношения и золотое сечение
Отношения и золотое сечение قدرمطلقی درجه اول
قدرمطلقی درجه اول Функции. ЕГЭ
Функции. ЕГЭ Текстовые задачи на движение по прямой
Текстовые задачи на движение по прямой Геометрическая вероятность
Геометрическая вероятность Призма. Прямая и наклонная призма. Правильная призма. Параллелепипед. Куб
Призма. Прямая и наклонная призма. Правильная призма. Параллелепипед. Куб Цифра 1. Посчитаем до 10
Цифра 1. Посчитаем до 10 Презентация на тему Деление обыкновенных дробей
Презентация на тему Деление обыкновенных дробей  Тригонометрия. Математическая игра АС-11
Тригонометрия. Математическая игра АС-11 ОГЭ 2020-21. Задание №13. Решение неравенства
ОГЭ 2020-21. Задание №13. Решение неравенства Что узнали. Чему научились
Что узнали. Чему научились Построение сечений многогранников
Построение сечений многогранников Задача о смесях
Задача о смесях