Содержание
- 2. Цель занятия: Изучить совокупность статистических показателей. Осознать их значение в формировании результатов статистического исследования План. Абсолютные
- 3. Третьим этапом статистического исследования является расчет, обобщение и анализ показателей. Важное место в системе обобщающих показателей
- 4. Абсолютная величина — объем или размер изучаемого события или явления, процесса, выраженного в соответствующих единицах измерения
- 5. Формы учета абсолютных величин: натуральный — физические единицы (штук, человек)- условно-натуральный — применяется при подсчете итогов
- 6. Натуральные единицы измерения бывают простыми и составными. Простые натуральные единицы измерения — это тонны, километры, штуки,
- 7. Относительные величины. Относительные величины представляют собой различные коэффициенты или проценты. Относительные статистические величины — это показатели,
- 8. Относительные величины могут быть выражены: - в коэффициентах, если база сравнения принимается за единицу ; -
- 9. Относительные величины, полученные в результате соотношения одноименных статистических показателей: 1. Относительная величина динамики — характеризует изменение
- 10. 2. Относительная величина планового задания. Рассчитывается как отношение уровня, запланированного на предстоящий период, к уровню, фактически
- 11. 4. Относительные величины структуры — характеризуют долю, отдельных частей в общем объеме совокупности и выражаются в
- 12. 6. Относительные величины сравнения (ОВСр) — сопоставляют размеры одноименных абсолютных величин, относящихся к одному и тому
- 13. Относительные величины, представляющие результат сопоставления разноименных статистических показателей 7. Относительные величины интенсивности (ОВИ) — характеризуют степень
- 14. Средние величины Средней величиной называется статистический показатель, который дает обобщенную характеристику варьирующего признака однородных единиц совокупности.
- 17. Показатели вариации При изучении варьирующего признака у единиц совокупности нельзя ограничиваться лишь расчетом средней величины из
- 18. Различают вариацию признака в абсолютных и относительных величинах. К абсолютным показателям относятся: размах вариации, среднее линейное
- 21. Мода и медиана наиболее часто используемые в экономической практике структурные средние Мода – это величина признака
- 22. Медианой называется такое значение признака, которое приходится на середину ранжированного ряда, т.е. в ранжированном ряду распределения
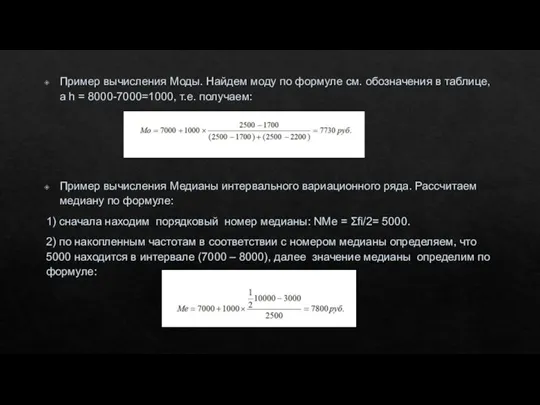
- 23. Пример: вычисления Моды и Медианы. Рассчитаем моду и медиану по данным табл. Таблица – Распределение семей
- 24. Пример вычисления Моды. Найдем моду по формуле см. обозначения в таблице, а h = 8000-7000=1000, т.е.
- 26. Скачать презентацию






















 Равносильность уравнений. 11 класс
Равносильность уравнений. 11 класс Прогрессии
Прогрессии Кривые второго порядка. Практика
Кривые второго порядка. Практика Эскизы кривых на плоскости, заданных параметрически
Эскизы кривых на плоскости, заданных параметрически Линейная алгебра просто! интерактивное учебное пособие
Линейная алгебра просто! интерактивное учебное пособие Среднее арифметическое. 5 класс
Среднее арифметическое. 5 класс Презентация на тему Симметрия. Осевая и центральная симметрии
Презентация на тему Симметрия. Осевая и центральная симметрии  Приведение дробей к общему знаменателю Молодых Наталья Андреевна Учитель математики средней школы № 3 г.Каменска- Уральского Св
Приведение дробей к общему знаменателю Молодых Наталья Андреевна Учитель математики средней школы № 3 г.Каменска- Уральского Св Двугранный угол. Перпендикулярность плоскостей
Двугранный угол. Перпендикулярность плоскостей Математический КВН
Математический КВН Преобразование графиков
Преобразование графиков Величины. Масса (1 класс)
Величины. Масса (1 класс)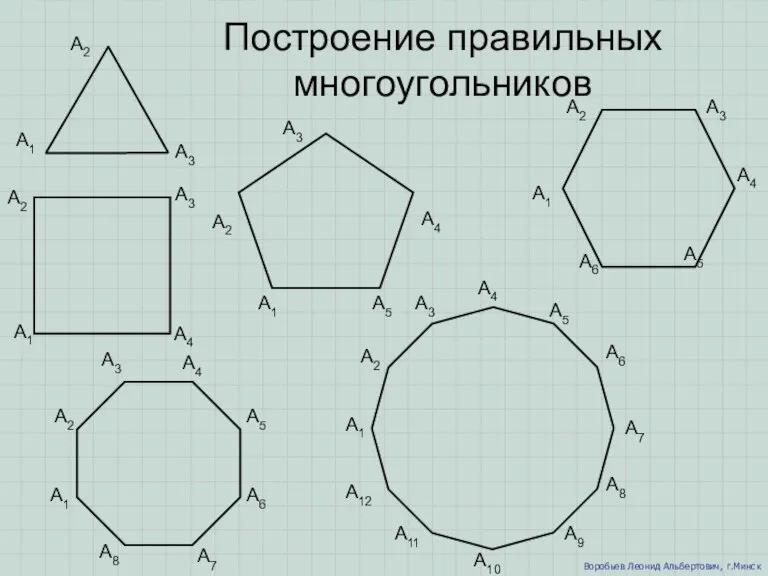 Построение правильных многоугольников
Построение правильных многоугольников Тест 3 по математике
Тест 3 по математике Рисунки из геометрических фигур
Рисунки из геометрических фигур Сравнение, сложение и вычитание дробей с разными знаменателями
Сравнение, сложение и вычитание дробей с разными знаменателями Сборник задач Во имя тех священных дней
Сборник задач Во имя тех священных дней Lek-AFK-Differentsialnye_uravnenia
Lek-AFK-Differentsialnye_uravnenia Геометрический смысл производной f '(x₀) = tg α = к
Геометрический смысл производной f '(x₀) = tg α = к Решение задач
Решение задач Квадратичная функция. Наглядно-методическое пособие. 9 класс
Квадратичная функция. Наглядно-методическое пособие. 9 класс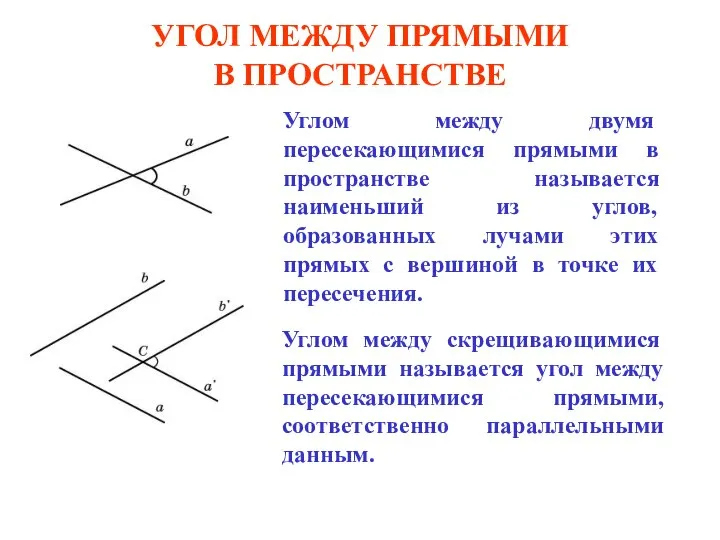 Угол между двумя прямыми в пространстве Вариант 2.ppt
Угол между двумя прямыми в пространстве Вариант 2.ppt Методы кластеризации
Методы кластеризации Без знаний дробей никто не может признаваться знающим арифметику
Без знаний дробей никто не может признаваться знающим арифметику Перпендикулярность прямых и плоскостей
Перпендикулярность прямых и плоскостей Презентация на тему ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ
Презентация на тему ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ  Интерактивный тренажер Подобные слагаемые
Интерактивный тренажер Подобные слагаемые Площадь фигуры. Сравнение площадей
Площадь фигуры. Сравнение площадей