Содержание
- 2. Cn – это число правильных расстановок n пар скобок. Пример: C0=1 C1=1 ( ) C2=2 ((
- 3. C3 = 5 Число путей = Cn Cn = Пути в квадрате ((( ))) (( )(
- 4. Дерево – связный граф без циклов Двоичное дерево – это такое дерево, у каждой вершины которого
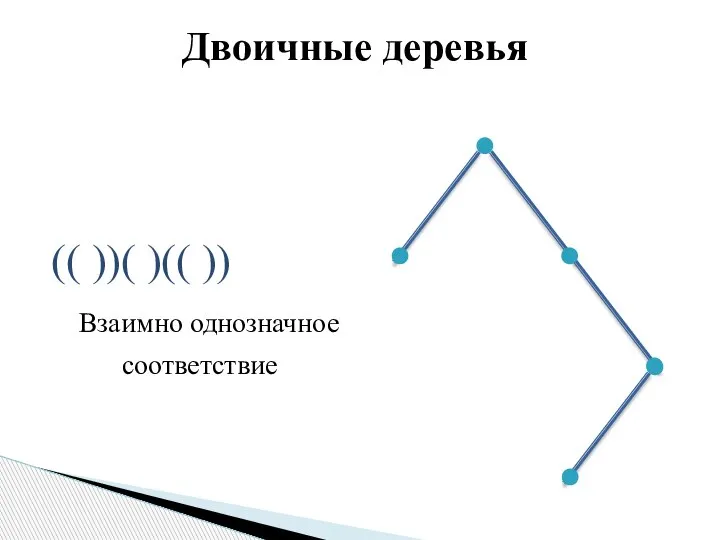
- 5. (( ))( )(( )) Взаимно однозначное соответствие Двоичные деревья
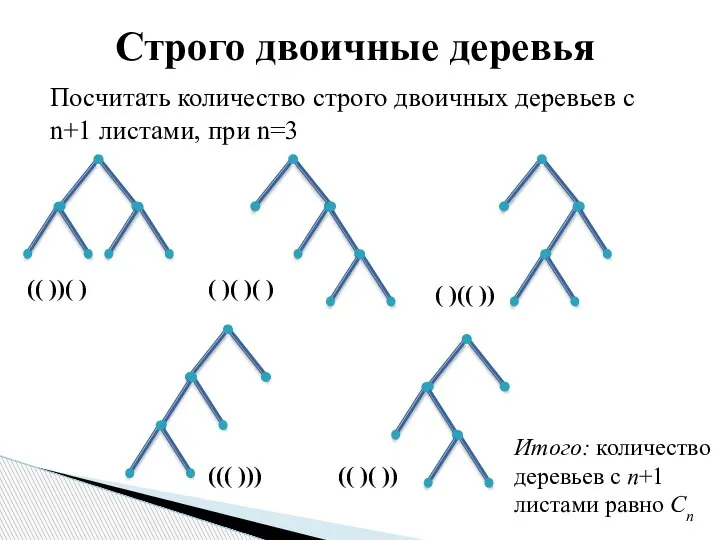
- 6. Посчитать количество строго двоичных деревьев с n+1 листами, при n=3 Строго двоичные деревья Итого: количество деревьев
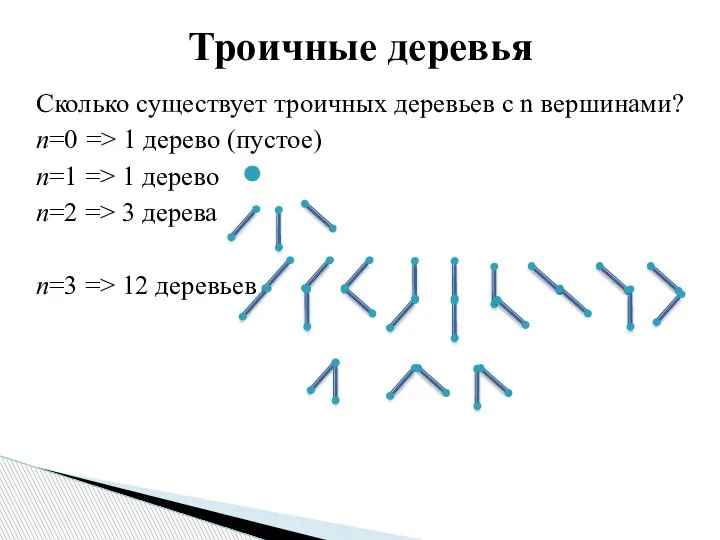
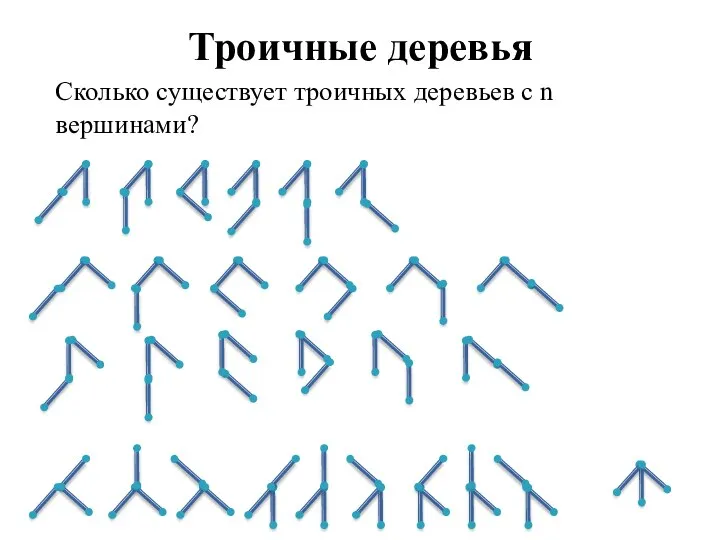
- 7. Сколько существует троичных деревьев с n вершинами? n=0 => 1 дерево (пустое) n=1 => 1 дерево
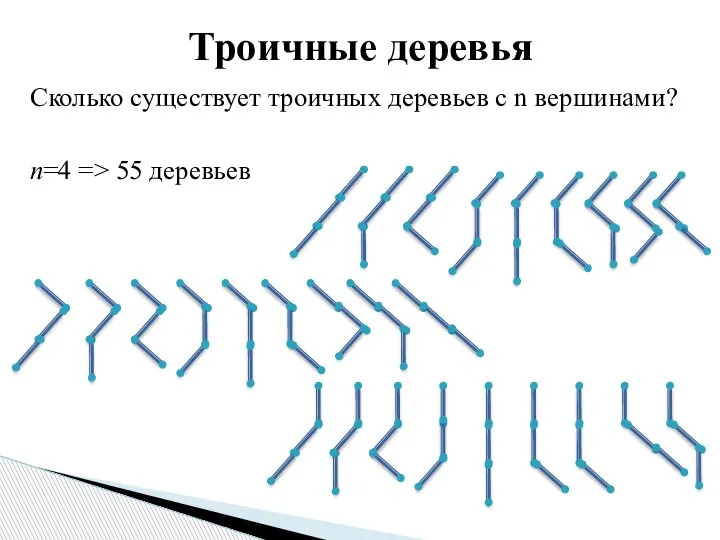
- 8. Сколько существует троичных деревьев с n вершинами? n=4 => 55 деревьев Троичные деревья
- 9. Сколько существует троичных деревьев с n вершинами? Троичные деревья
- 10. Tn – всего троичных деревьев с n вершинами. Троичные деревья
- 11. сn(p, r) = Пример: сn(2, 1) = = = сn Теорема: Tn = сn(3, 1) =
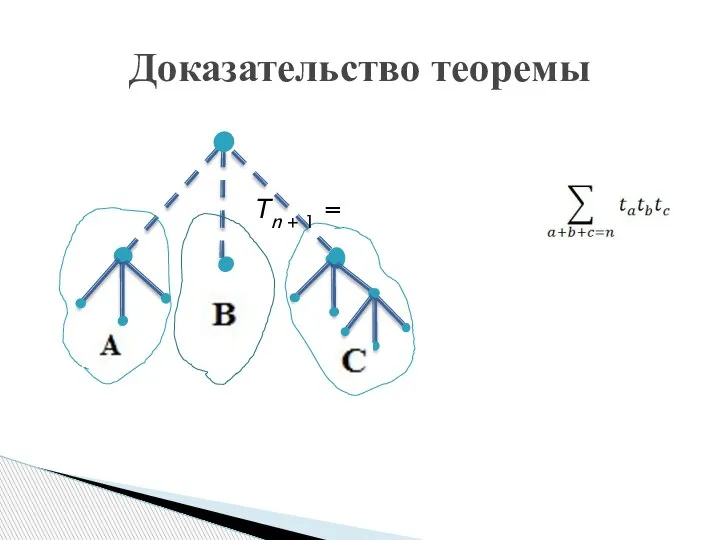
- 12. tn = сn(3, 1) tn + 1 = , t0 = 1 Тn + 1 =
- 13. Доказательство теоремы Тn + 1 =
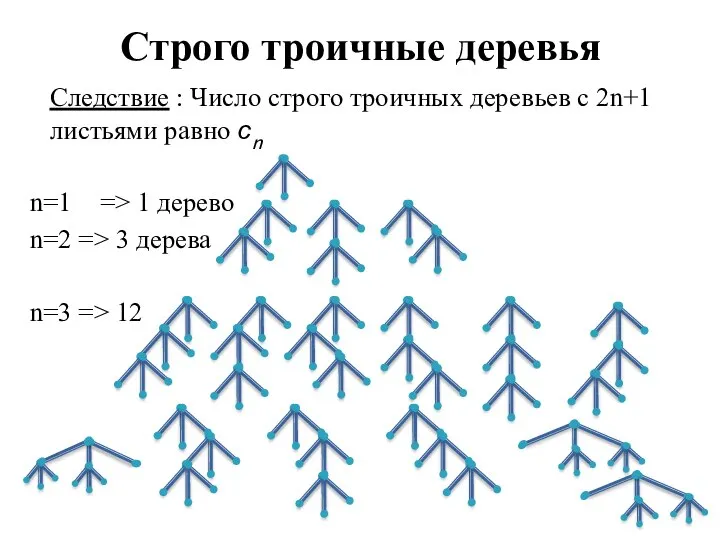
- 14. Следствие : Число строго троичных деревьев с 2n+1 листьями равно сn n=1 => 1 дерево n=2
- 16. Скачать презентацию






 Геометрическое шоу Десять пятерок
Геометрическое шоу Десять пятерок Sie hat Geburtstag am fünften August. Er kommt am einunddreißigsten Juli
Sie hat Geburtstag am fünften August. Er kommt am einunddreißigsten Juli Решение планиметрических задач
Решение планиметрических задач Презентация по математике "УУД, которые формируются у ученика в процессе изучения математики в 4 классе" -
Презентация по математике "УУД, которые формируются у ученика в процессе изучения математики в 4 классе" -  Деление взаимно обратных чисел
Деление взаимно обратных чисел Презентация на тему Геометрические фигуры (2 класс)
Презентация на тему Геометрические фигуры (2 класс)  Пирамида. Элементы пирамиды
Пирамида. Элементы пирамиды Весёлые клоуны. Игра по математике для 1 класса
Весёлые клоуны. Игра по математике для 1 класса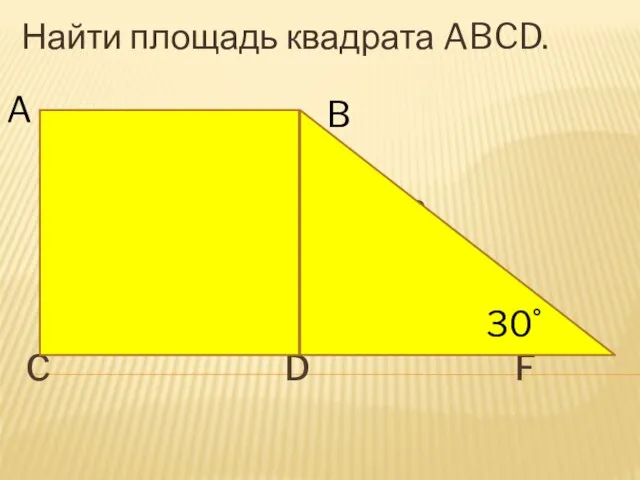 Решение задач. Площадь квадрата
Решение задач. Площадь квадрата Приложения производной
Приложения производной Презентация на тему Состав числа 5
Презентация на тему Состав числа 5  Построение сечений тетраэдра
Построение сечений тетраэдра Параллельность в пространстве
Параллельность в пространстве Наука Метрология
Наука Метрология Угол. Луч
Угол. Луч Презентация на тему Противоположные числа (6 класс)
Презентация на тему Противоположные числа (6 класс)  Логические и традиционные головоломки
Логические и традиционные головоломки Умножение натуральных чисел
Умножение натуральных чисел Тренажер. Примеры
Тренажер. Примеры Логарифмы
Логарифмы Потенцирование логарифмических выражений
Потенцирование логарифмических выражений Презентация на тему Разложение многочлена на множители 7 класс
Презентация на тему Разложение многочлена на множители 7 класс  Урок по теме Многочлен и его стандартный вид
Урок по теме Многочлен и его стандартный вид Презентация на тему Решение задач на построение сечений многогранников
Презентация на тему Решение задач на построение сечений многогранников  Среднее арифметическое
Среднее арифметическое Элементы векторной алгебры
Элементы векторной алгебры ТРАПЕЦІЯ
ТРАПЕЦІЯ Игра 7
Игра 7