Содержание
- 2. Евтушенко Ирина Ивановна Доклад на РМО математиков 2009 год Г. Дальнегорск Приморский край
- 3. Равенство вида f(x)=g(x), уравнение с одним неизвестным.
- 4. Число a называется корнем уравнения если обе части уравнения определены при x=a равенство f(a)=g(a) является верным.
- 5. Решить уравнение – значит найти все его корни или доказать, что корней нет.
- 6. В процессе решения часто приходится преобразовывать уравнение, заменяя его более простым. Нельзя выполнять преобразования, которые приводят
- 7. Определение. Уравнения f(x) = g(x) и p(x) = h(x) называются равносильными, если совпадают множества их корней.
- 8. Теоремы о равносильности уравнений Теорема 1. Если какой-нибудь член уравнения перенести из одной части уравнения в
- 9. Теорема 4. Если обе части уравнения f(x) = g(x) умножить на выражение h(x), которое имеет смысл
- 10. Общие приемы решения уравнений
- 11. Метод разложения на множители Этот метод заключается в том, что уравнение f(x)g(x)h(x) = 0 можно заменить
- 12. Метод замены переменной Этот метод заключается в том, что если уравнение f(x) = 0 сводится к
- 13. Использование свойств функций Пусть у нас имеется уравнение f(x) = g(x). Если одна из функций возрастает,
- 14. Показательные уравнение Основным методом решения показательных уравнений является сведение уравнения с помощью различных преобразований правой и
- 15. Уравнение с иррациональностью Основным методом решения уравнения с иррациональностью является приведение уравнения с помощью различных преобразований
- 16. По результатам ЕГЭ 2008 года выявились недочеты при выполнении работы.
- 17. Оказалось что выпускники, получившие оценку «3»: не научились решать иррациональные и тригонометрические уравнения
- 18. Проиллюстрируем конкретными примерами, какие недочеты выявились у «хорошистов» при выполнении заданий повышенного уровня сложности. Они успешно
- 19. Более низкие результаты показаны этими учащимися при выполнении «похожего» уравнения (см. пример 3).
- 20. Это наблюдение подтверждается и при анализе результатов выполнения заданий повышенного уровня с развернутым ответом (С1-С2). Как
- 22. Скачать презентацию



















 Простейшие свойства линейных пространств. Линейная зависимость и независимость
Простейшие свойства линейных пространств. Линейная зависимость и независимость Геометрические фигуры
Геометрические фигуры Сложение отрицательных чисел
Сложение отрицательных чисел Координатная плоскость
Координатная плоскость Площадь параллелограмма
Площадь параллелограмма Квадратный корень
Квадратный корень Презентация на тему Государственная политика противодействия наркотизму
Презентация на тему Государственная политика противодействия наркотизму  Решение логарифмических уравнений
Решение логарифмических уравнений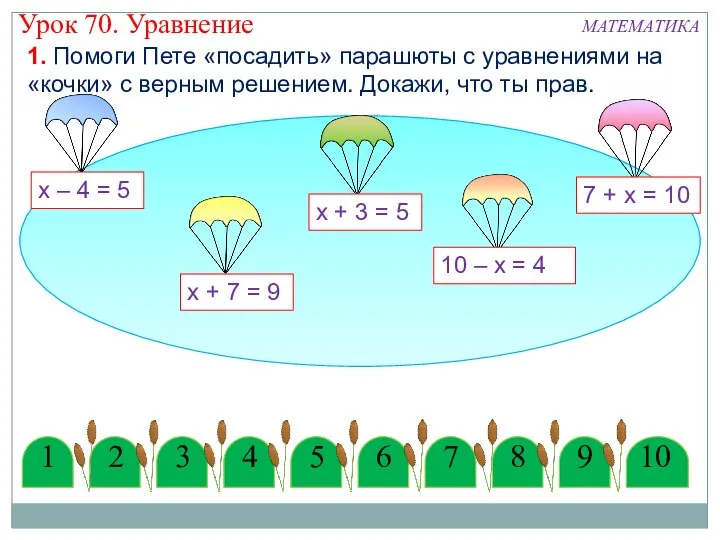 Уравнение. Математика. Урок 70
Уравнение. Математика. Урок 70 Квадратный трёхчлен. Решение задач
Квадратный трёхчлен. Решение задач Числовые последовательности
Числовые последовательности Корень уравнения
Корень уравнения Арифметическая прогрессия
Арифметическая прогрессия Готовимся к ОГЭ по математике
Готовимся к ОГЭ по математике Метод координат на плоскости
Метод координат на плоскости Китайская математика
Китайская математика Подготовка к итоговой аттестации
Подготовка к итоговой аттестации Генеалогическое древо семьи Бернулли
Генеалогическое древо семьи Бернулли Решение задач на проценты
Решение задач на проценты Отображение. Отражение относительно прямой. Преобразование единичного квадрата
Отображение. Отражение относительно прямой. Преобразование единичного квадрата математика
математика Основное свойство дроби
Основное свойство дроби Окружность. Построение серединного перпендикуляра
Окружность. Построение серединного перпендикуляра Задачи на нахождение элементов призмы
Задачи на нахождение элементов призмы Некоторые приемы решения целых уравнений
Некоторые приемы решения целых уравнений Однородные тригонометрические уравнения
Однородные тригонометрические уравнения Квадратные корни
Квадратные корни Копилка интересных идей и находок
Копилка интересных идей и находок