Аксиома параллельных прямых

ЦЕЛЬ УРОКА:
Познакомить с понятием аксиомы в геометрии
Организация деятельности обучающихся по изучению и первичному закреплению аксиомы параллельных прямых и её следствий.

Теорема – утверждение , для которого в рассматриваемой теории существует доказательство.
Следствие – утверждение, которое выводится из теорем и аксиом.
Теорема и следствие

АКСИОМА
Что это такое?
Как произошло?

Аксиома
Это исходные положения, на основе, которых доказываются далее теоремы и строится вся геометрия.
Происходит от греческого «аксиос»,
что означает «ценный, достойный».

Некоторые аксиомы были сформулированы еще в первой главе
(хотя они и не назывались там аксиомами).

Через любые две точки
проходит прямая, и притом
только одна

На любом луче от его начала можно отложить отрезок, равный данному, и
притом только один

От любого луча в заданную сторону можно отложить угол, равный данному неразвернутому углу, и притом только один

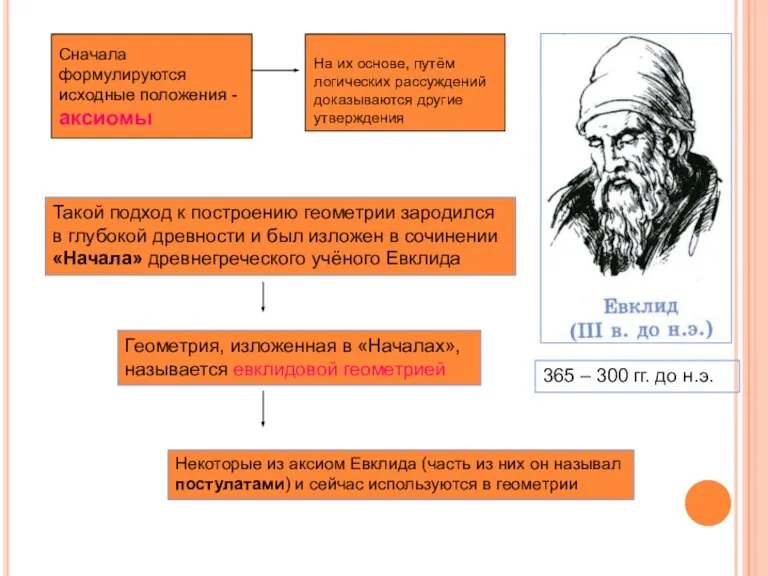
Сначала формулируются исходные положения - аксиомы
На их основе, путём логических рассуждений доказываются другие утверждения
Такой подход к построению геометрии зародился в глубокой древности и был изложен в сочинении «Начала» древнегреческого учёного Евклида
365 – 300 гг. до н.э.
Геометрия, изложенная в «Началах», называется евклидовой геометрией
Некоторые из аксиом Евклида (часть из них он называл постулатами) и сейчас используются в геометрии

ЗАДАЧА
Всегда ли через точку , не лежащую на данной прямой, можно провести параллельную прямую?
Сколько параллельных прямых можно провести через данную точку?

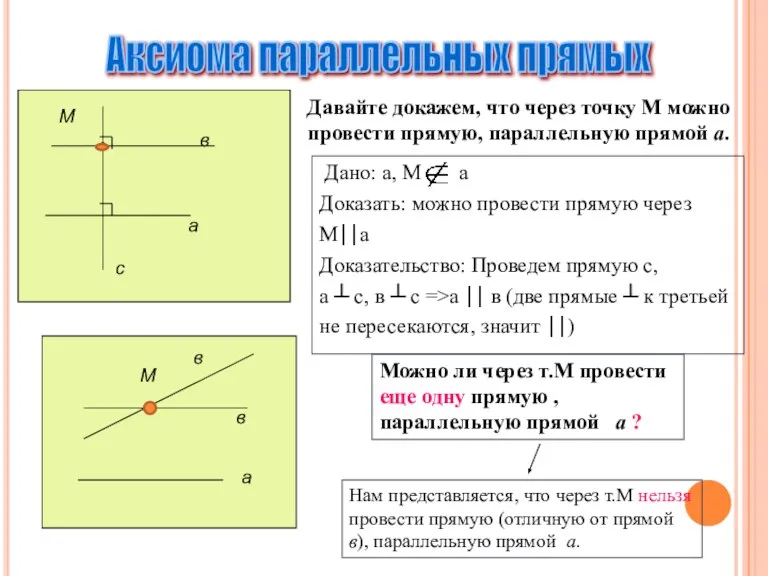
Аксиома параллельных прямых
М
а
в
с
Давайте докажем, что через точку М можно провести прямую, параллельную прямой а.
Дано: а, М а
Доказать: можно провести прямую через М⎪⎪а
Доказательство: Проведем прямую с,
а ┴ с, в ┴ с =>а ⎪⎪ в (две прямые ┴ к третьей не пересекаются, значит ⎪⎪)
Можно ли через т.М провести еще одну прямую , параллельную прямой а ?
в
в
а
М
Нам представляется, что через т.М нельзя провести прямую (отличную от прямой в), параллельную прямой а.

Аксиома параллельных прямых
Можно ли это утверждение доказать?
Огромную роль в решении этого непростого вопроса сыграл великий русский математик Николай Иванович Лобачевский
Он выяснил, что это утверждение доказать нельзя, т.к. само является аксиомой.

Аксиома параллельных прямых
Через точку, не лежащую на данной
прямой, проходит только одна
прямая, параллельная данной.
а
b
М

«Через точку, не лежащую на данной прямой,
проходит только одна прямая, параллельная
данной».
«Через точку, не лежащую на данной прямой, можно провести прямую, параллельную данной».
Какое из данных утверждений является аксиомой?
Чем отличаются вышеуказанные утверждения ?

1. Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
Следствия из аксиомы параллельных прямых
Доказательство: (методом от противного)
Предположим, что прямая с не пересекает прямую в, значит, с в.
Тогда через т.М проходят две прямые а и с параллельные прямой в.
3. Но это противоречит аксиоме параллельных прямых, значит, прямая с пересекает прямую в.

2.Если две прямые параллельны третьей прямой, то они параллельны.
Следствия из аксиомы параллельных прямых
Доказательство: (методом от противного)
Предположим, что прямая а и прямая в пересекаются.
2. Тогда через т.М проходят две прямые а и в параллельные прямой с
3 . Но это противоречит аксиоме параллельных прямых.
4. Значит прямые а и в параллельны.

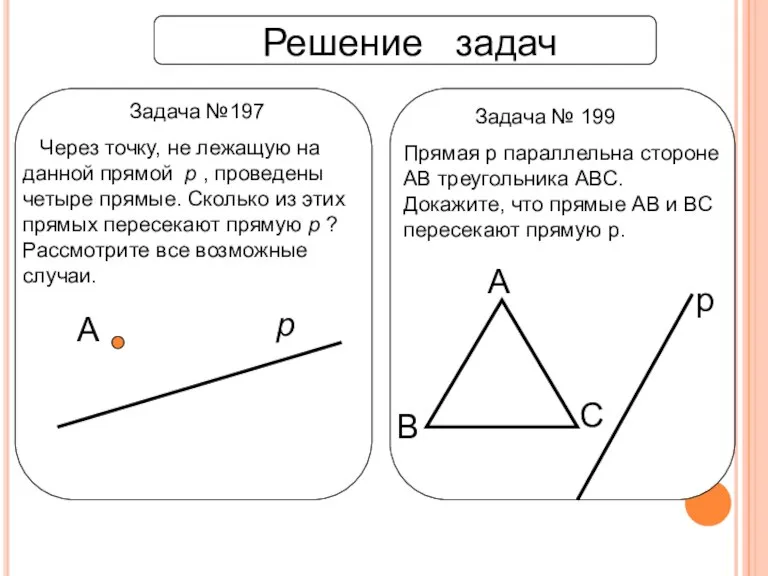
Решение задач
Задача №197
Через точку, не лежащую на данной прямой p , проведены четыре прямые. Сколько из этих прямых пересекают прямую p ? Рассмотрите все возможные случаи.
А
р
Задача № 199
Прямая р параллельна стороне АВ треугольника АВС. Докажите, что прямые АВ и ВС пересекают прямую р.
А
В
С
р

Закончи предложение:
Исходные утверждения о свойствах
геометрических фигур называются …
Через точку, не лежащую на данной прямой …
Если прямая пересекает одну из двух
параллельных прямых, то ….
Если две прямые параллельны третьей, то ….