Содержание
- 2. Непрерывность
- 3. Свойства функций, непрерывных в точке
- 4. Непрерывность на отрезке Если функция y=f(x) непрерывна на отрезке [a,b], то она ограничена на этом отрезке
- 5. Точки разрыва Если функция f определена на полуинтервале (a-δ,a] и f(a-0)=f(a), то функция f непрерывна слева
- 6. Точки разрыва 1 рода
- 7. Точка разрыва 2 рода Пусть х=а –точка разрыва функции f, не являющаяся точкой разрыва 1 рода.
- 9. Скачать презентацию


![Непрерывность на отрезке Если функция y=f(x) непрерывна на отрезке [a,b], то она](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/978640/slide-3.jpg)
![Точки разрыва Если функция f определена на полуинтервале (a-δ,a] и f(a-0)=f(a), то](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/978640/slide-4.jpg)


 Решение дифференциальных уравнений методом ломаных Эйлера с использованием электронных таблиц MS Excel
Решение дифференциальных уравнений методом ломаных Эйлера с использованием электронных таблиц MS Excel Ряды распределения в статистике
Ряды распределения в статистике Отношение. Пропорция
Отношение. Пропорция Элементы теории вероятности
Элементы теории вероятности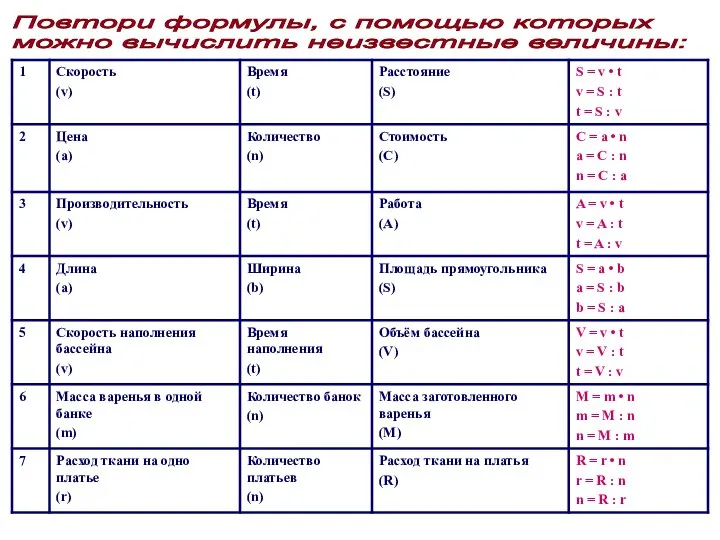 Скорость (v), Время (t), Расстояние (S)
Скорость (v), Время (t), Расстояние (S) Аксиомы стереометрии. Некоторые следствия из аксиом
Аксиомы стереометрии. Некоторые следствия из аксиом Вокруг квадратного трёхчлена
Вокруг квадратного трёхчлена Старинные задачи с использованием дробей
Старинные задачи с использованием дробей Центральные углы и углы, вписанные в окружность
Центральные углы и углы, вписанные в окружность Тройные интегралы в цилиндрических координатах
Тройные интегралы в цилиндрических координатах Структура урока
Структура урока Стереометрия. Многогранники
Стереометрия. Многогранники Презентация на тему Натуральные числа
Презентация на тему Натуральные числа  Основы факторного моделирования безопасности систем вида защита – объект – среда
Основы факторного моделирования безопасности систем вида защита – объект – среда Понятие логарифма
Понятие логарифма Евклид. Детство и ранние годы
Евклид. Детство и ранние годы Презентация на тему Делители и кратные
Презентация на тему Делители и кратные  Подготовка к ЕГЭ. Графическое решение уравнений и неравенств
Подготовка к ЕГЭ. Графическое решение уравнений и неравенств Станция Игровая. Занимательная математика
Станция Игровая. Занимательная математика Готовимся к ЕГЭ. Базовый уровень
Готовимся к ЕГЭ. Базовый уровень Позиция 7 ЕГЭ 2016. Физический смысл производной
Позиция 7 ЕГЭ 2016. Физический смысл производной Оценки параметров распределения. Статистические оценки
Оценки параметров распределения. Статистические оценки Пример проектной работы. Зимние олимпийские игры. Общая статистика
Пример проектной работы. Зимние олимпийские игры. Общая статистика Векторная алгебра. Лекция 4
Векторная алгебра. Лекция 4 Тригонометрические уравнения и математические термины на английском языке
Тригонометрические уравнения и математические термины на английском языке Решение задач Параллельные прямые
Решение задач Параллельные прямые Однозначные и двузначные числа
Однозначные и двузначные числа Операции над графами
Операции над графами