Содержание
- 2. Аксиомы стереометрии – утверждения о свойствах геометрических тел, принимаемые в качестве исходных положений, на основе которых
- 3. Если C ∉ AB, то ∃α: A, B, C ∊ α, причем α – единственная.
- 4. Аксиома A2 Если две точки прямой лежат в плоскости, то все точки этой прямой лежат в
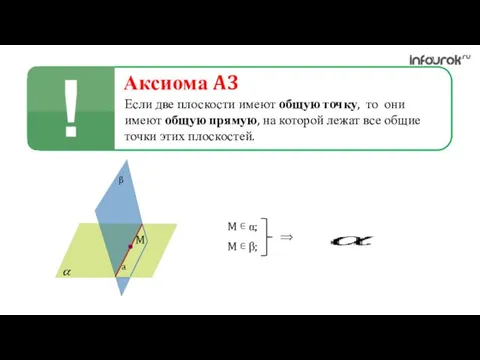
- 5. Аксиома A3 Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат
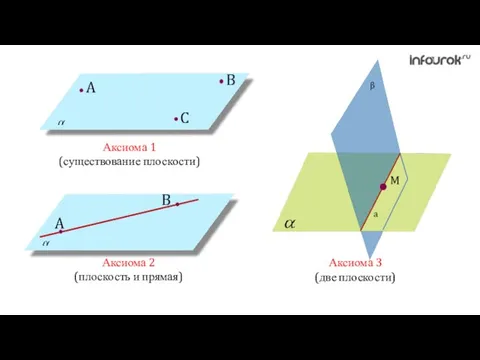
- 6. Аксиома 1 (существование плоскости) Аксиома 2 (плоскость и прямая) Аксиома 3 (две плоскости)
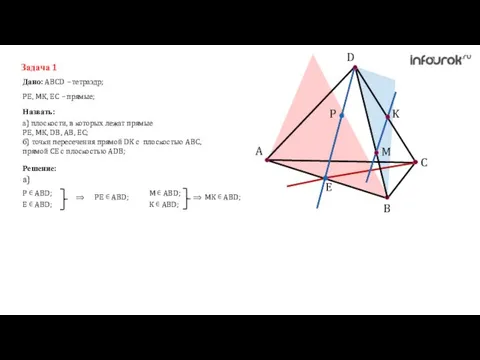
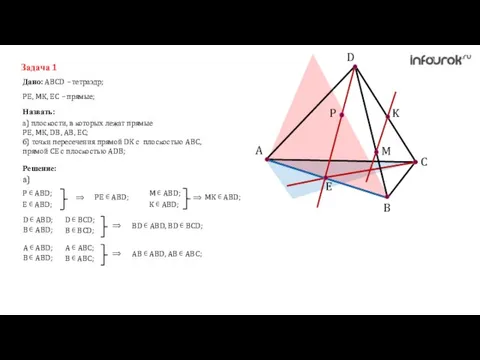
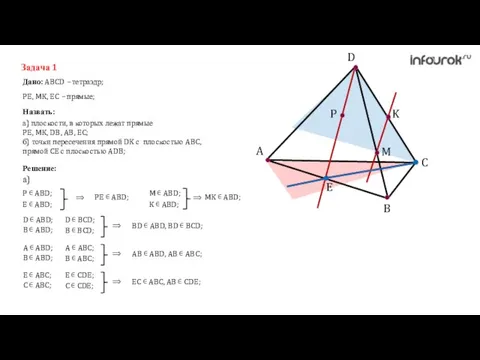
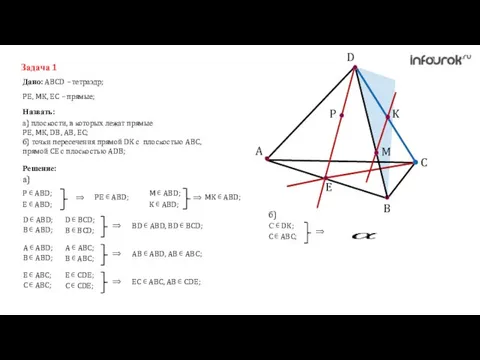
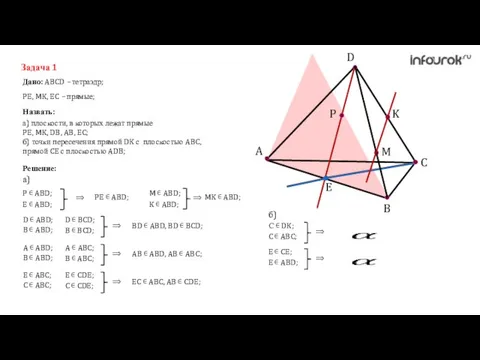
- 7. A C B D K M P E Задача 1 Дано: ABCD – тетраэдр; Назвать: PE,
- 8. A C B D K M P E Задача 1 Дано: ABCD – тетраэдр; Назвать: PE,
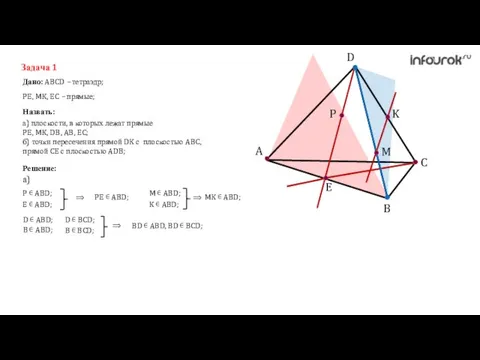
- 9. A C B D K M P E Задача 1 Дано: ABCD – тетраэдр; Назвать: PE,
- 10. A C B D K M P E Задача 1 Дано: ABCD – тетраэдр; Назвать: PE,
- 11. A C B D K M P E Задача 1 Дано: ABCD – тетраэдр; Назвать: PE,
- 12. A C B D K M P E Задача 1 Дано: ABCD – тетраэдр; Назвать: PE,
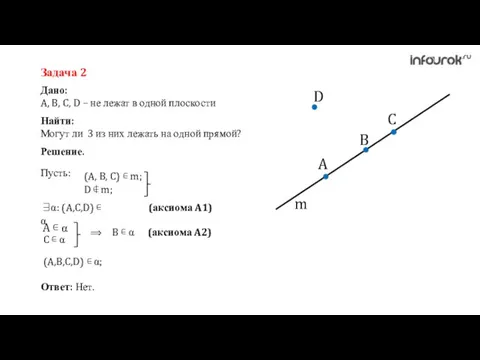
- 13. Дано: A, B, C, D – не лежат в одной плоскости Задача 2 Найти: Могут ли
- 15. Скачать презентацию



 Геометрия. Построение сечений
Геометрия. Построение сечений Геометрия. Заготовка
Геометрия. Заготовка Элементы математической статистики
Элементы математической статистики Устойчивость движения. Фазовая плоскость. Классификация точек покоя
Устойчивость движения. Фазовая плоскость. Классификация точек покоя Функция. Свойства функции (10 класс)
Функция. Свойства функции (10 класс) Решение систем неравенств (8 класс)
Решение систем неравенств (8 класс) Решение задач на проценты. 7 класс
Решение задач на проценты. 7 класс Презентация по математике "Логарифмическая функция. Преобразования графиков." -
Презентация по математике "Логарифмическая функция. Преобразования графиков." -  Дифференциальные уравнения первого порядка. Дифференциальные уравнения с разделяющимися переменными
Дифференциальные уравнения первого порядка. Дифференциальные уравнения с разделяющимися переменными 1 урок. Аксиомы стереометрии
1 урок. Аксиомы стереометрии ПГНИУ-20.09.22 МЛ Л 4
ПГНИУ-20.09.22 МЛ Л 4 Подбираем наибольшее произведение
Подбираем наибольшее произведение Комплексные числа
Комплексные числа Выбор рационального пути решения задач
Выбор рационального пути решения задач Урок - путешествие. Математика (1 класс)
Урок - путешествие. Математика (1 класс) Презентация на тему ГИА-2013г. Модуль АЛГЕБРА №6
Презентация на тему ГИА-2013г. Модуль АЛГЕБРА №6  Тригонометрические и Логарифмические уравнения. Объёмы тел
Тригонометрические и Логарифмические уравнения. Объёмы тел Перпендикулярные прямые
Перпендикулярные прямые Деление трехзначного числа на двухзначное число
Деление трехзначного числа на двухзначное число Предел последовательности. Урок 1
Предел последовательности. Урок 1 Вероятность распределения случайных чисел
Вероятность распределения случайных чисел Вентцель Е.С. Теория вероятностей
Вентцель Е.С. Теория вероятностей Нахождение числа по его части. (6 класс. Тест №15)
Нахождение числа по его части. (6 класс. Тест №15) Формулы приведения
Формулы приведения Сложение и вычитание дробей с разными знаменателями
Сложение и вычитание дробей с разными знаменателями Презентация на тему Квадратный корень из произведения
Презентация на тему Квадратный корень из произведения  Вычисление плошади поверхности многраников
Вычисление плошади поверхности многраников Trapetsia
Trapetsia