Содержание
- 2. Транспортная задача задача о поиске оптимального распределения поставок однородного товара от поставщиков к потребителям при известных
- 3. Метод северо – западного угла Метод состоит в последовательном переборе строк и столбцов транспортной таблицы, начиная
- 4. Пример
- 5. Для решения задачи необходимо выполнение следующего условия: cуммарные запасы продукции у поставщиков должны равняться суммарной потребности
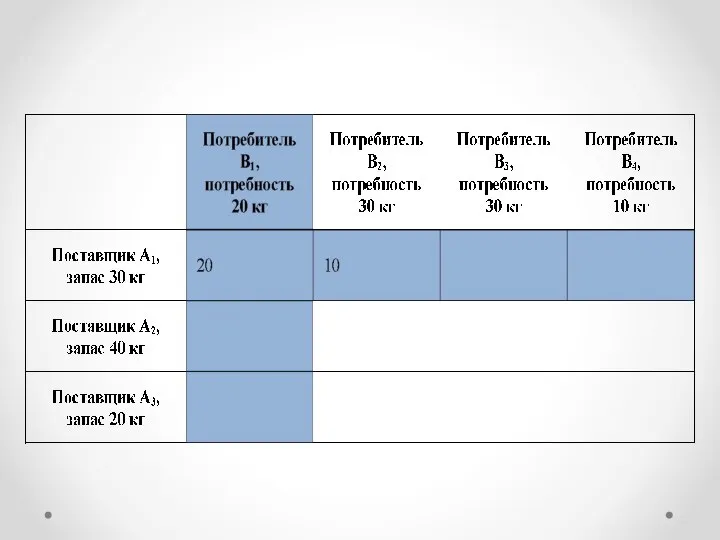
- 6. Шаг 1 Первая ячейка — с которой начинается распределение —будет «северо-западная» ячейка в левом верхнем углу
- 8. Шаг 2 Переходим в следующую «северо-западную» ячейку. Этой ячейкой будетX12 (1-й поставщик, 2-й потребитель). Вписываем в
- 10. Шаг 3 Переходим в следующую «северо-западную» ячейку, не считая окрашенной. Вписываем в эту ячейку максимальный объем,
- 12. 4 шаг
- 13. Шаг 5. Распределение оставшихся запасов по поставщикам. Z=40+30+40+100+20=60=290
- 14. Метод минимального элемента правило минимальных затрат — алгоритм получения допустимого начального решения транспортной задачи . В
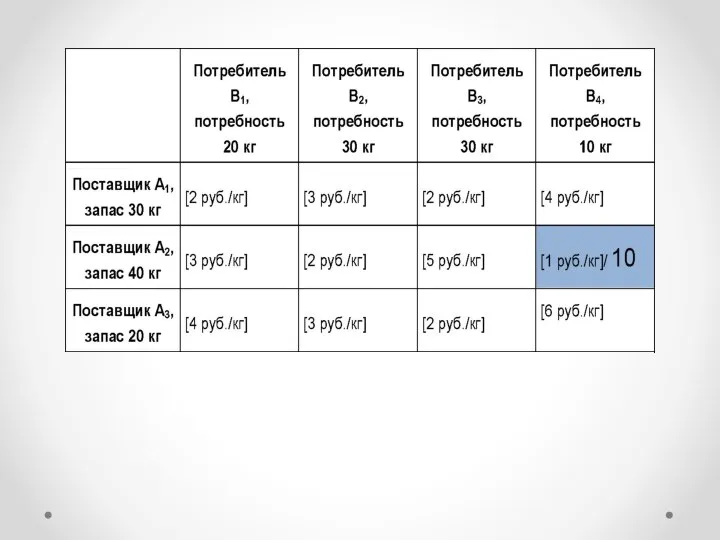
- 15. Шаг 1 Находим ячейку с минимальной ценой и вписываем в нее максимально возможный объем, который позволяет
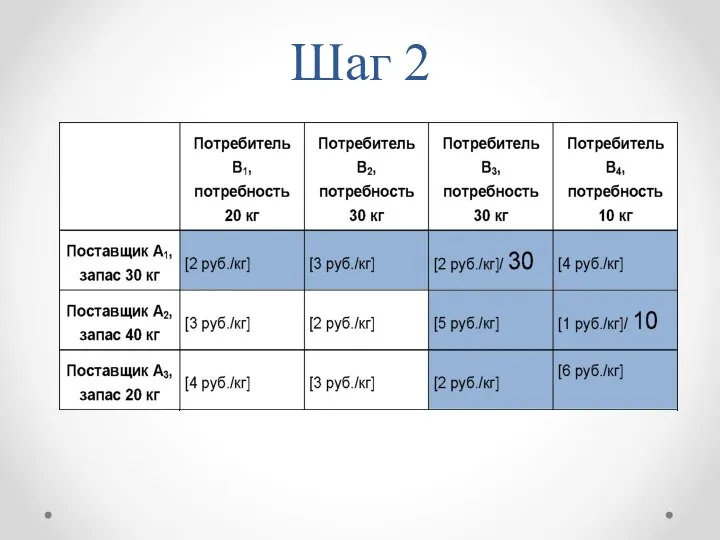
- 17. Шаг 2
- 18. Шаг 3 Z=20*4+2*30+2*30+10=210
- 19. Задача
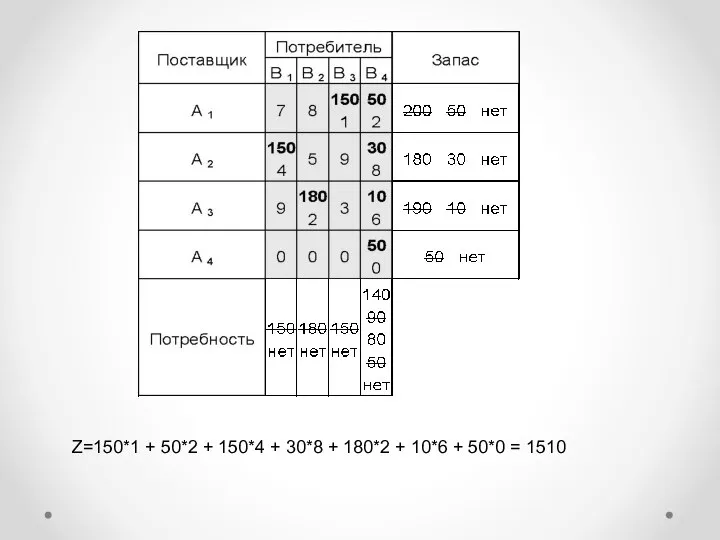
- 20. Решение Запасы поставщиков: 200 + 180 + 190 = 570 единиц продукции. Потребность потребителей: 150 +
- 21. Z=150*1 + 50*2 + 150*4 + 30*8 + 180*2 + 10*6 + 50*0 = 1510
- 22. Вопросы 1. Перечислите методы решения транспортной задачи 2. Что делать если спрос и предложение не совпадают?
- 24. Скачать презентацию

















 Круговые диаграммы
Круговые диаграммы Решение примеров и задач с числами, полученными при измерении стоимости
Решение примеров и задач с числами, полученными при измерении стоимости Свойства равнобедренного треугольника
Свойства равнобедренного треугольника Методика изучения геометрического материала
Методика изучения геометрического материала Логические задачи. Задачи со спичками
Логические задачи. Задачи со спичками Функция y = x2 и её график
Функция y = x2 и её график Признаки равенства треугольников
Признаки равенства треугольников Соотношения между сторонами и углами в произвольном треугольнике
Соотношения между сторонами и углами в произвольном треугольнике Графики и диаграммы. Задания
Графики и диаграммы. Задания Числовые выражения
Числовые выражения Линейная алгебра. Система линейных однородных уравнений. Фундаментальная система решений
Линейная алгебра. Система линейных однородных уравнений. Фундаментальная система решений Карточки с цифрами
Карточки с цифрами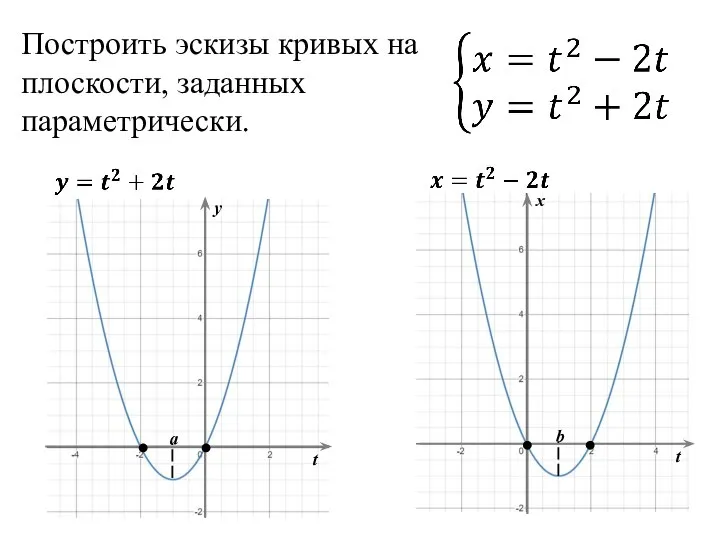 Построить эскизы кривых на плоскости, заданных параметрически
Построить эскизы кривых на плоскости, заданных параметрически Векторы в пространстве
Векторы в пространстве Геометрия. Решение задач
Геометрия. Решение задач Выполните деление
Выполните деление Признаки подобия треугольников
Признаки подобия треугольников Численные методы решения СЛАУ (часть 1)
Численные методы решения СЛАУ (часть 1) Площадь поверхности прямоугольного параллелепипеда
Площадь поверхности прямоугольного параллелепипеда Фотоальбом. Ребус
Фотоальбом. Ребус Сдвиг графика функции у = ах² вдоль осей координат
Сдвиг графика функции у = ах² вдоль осей координат Геометрия вокруг нас
Геометрия вокруг нас Замена двузначного числа суммой разрядных слагаемых
Замена двузначного числа суммой разрядных слагаемых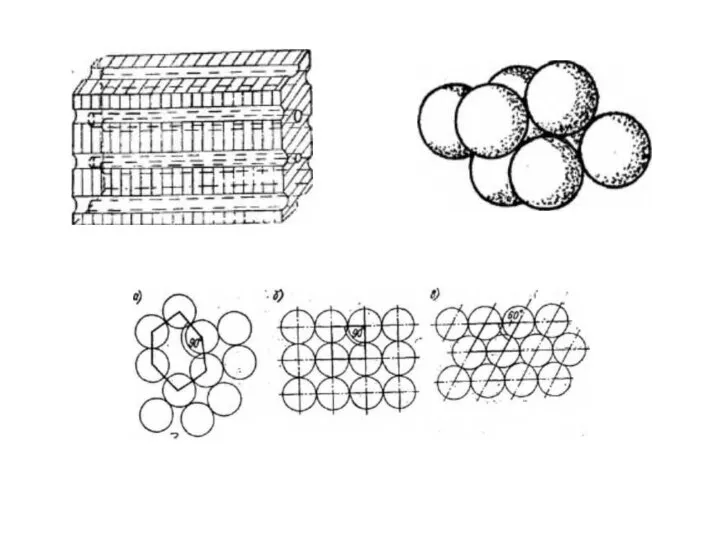 Кристаллическая решетка. Уравнения производной
Кристаллическая решетка. Уравнения производной Векторы
Векторы Кривые, заданные параметрически
Кривые, заданные параметрически Решение задач
Решение задач Устные и письменные приемы умножения
Устные и письменные приемы умножения