Содержание
- 2. Теорема Муавра-Лапласа При большом числе испытаний n в схеме Бернулли число успехов k имеет приближенно нормальное
- 3. Теорему можно использовать для приближенного расчета вероятности того, что число успехов лежит в заданном диапазоне При
- 4. Пример При данном технологическом процессе 90% всей произведенной продукции является высшим сортом. Произведено 4000 изделий. Какова
- 5. Проводится n=4000 испытаний. Успех – изделие высшего сорта, p=0,9, q=0,1. По условию задачи, надо найти Решение:
- 6. Проводится n=4000 испытаний. Успех – изделие высшего сорта, p=0,9, q=0,1. По условию задачи, надо найти Решение:
- 7. Проводится n=4000 испытаний. Успех – изделие высшего сорта, p=0,9, q=0,1. По условию задачи, надо найти Решение:
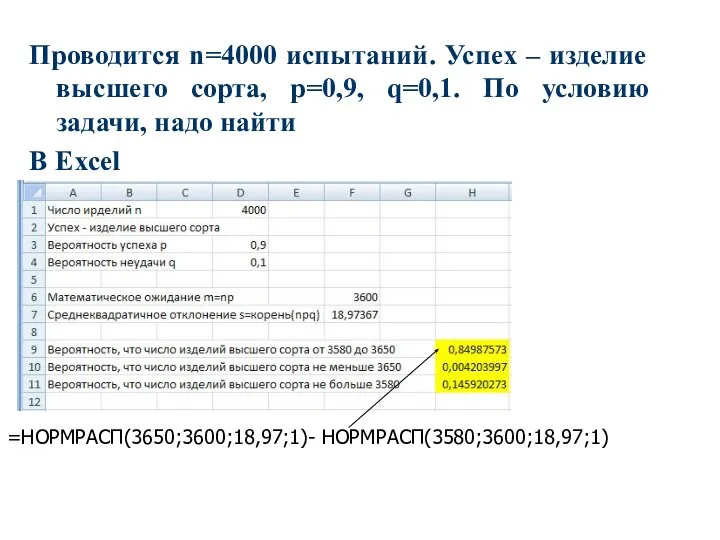
- 8. Проводится n=4000 испытаний. Успех – изделие высшего сорта, p=0,9, q=0,1. По условию задачи, надо найти В
- 9. В институте обучается 1000 студентов. В столовой имеется 105 посадочных мест. Каждый студент отправляется в столовую
- 10. Проводится n=1000 испытаний. Успех – поход в столовую p=0,1, q=0,9. По условию задачи, надо найти Решение:
- 11. В институте обучается 1000 студентов. В столовой имеется 105 посадочных мест. Каждый студент отправляется в столовую
- 12. Проводится n=1000 испытаний. Успех – поход в столовую p=0,1, q=0,9. По условию задачи, надо найти Решение:
- 13. Решение в Excel =НОРМРАСП(105;100;9.487;1)
- 14. В институте обучается 1000 студентов. В столовой имеется 105 посадочных мест. Каждый студент отправляется в столовую
- 15. Пусть в столовой М мест. По условию задачи, Решение:
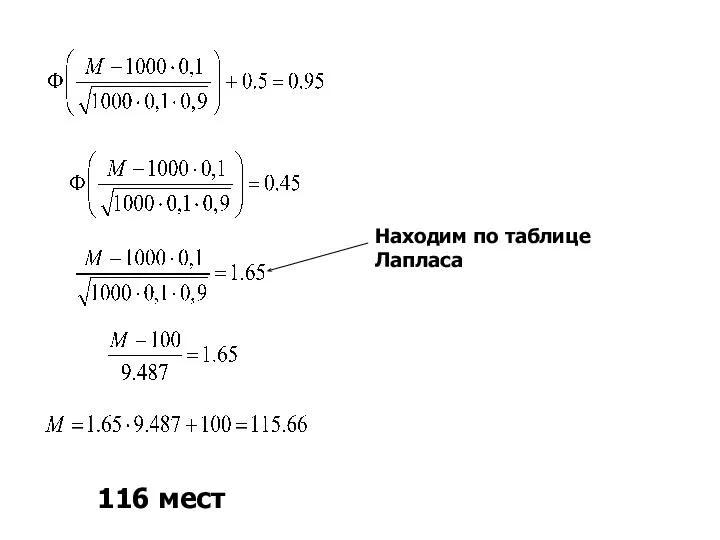
- 16. Находим по таблице Лапласа 116 мест
- 18. Скачать презентацию













 Презентация на тему Части сферы и шара
Презентация на тему Части сферы и шара  Федеральный интернет-экзамен. Дифференцирование
Федеральный интернет-экзамен. Дифференцирование Прямая и плоскость
Прямая и плоскость Математическая разминка
Математическая разминка Теорема Пифагора
Теорема Пифагора Элективный курс Решение планиметрических задач на вписанные и описанные окружности
Элективный курс Решение планиметрических задач на вписанные и описанные окружности Функция y=sin x, её свойства и график
Функция y=sin x, её свойства и график Арифметический диктант
Арифметический диктант Предел функции в точке
Предел функции в точке Решение логических задач
Решение логических задач проект Артюшина
проект Артюшина Системы булевых функций. Лекция 5
Системы булевых функций. Лекция 5 Площади многоугольников
Площади многоугольников Повторим правила образования и записи чисел
Повторим правила образования и записи чисел Подобные слагаемые
Подобные слагаемые Знакомство с линиями чертежа. Наклонная
Знакомство с линиями чертежа. Наклонная Совокупность математических методов для изучения свойств кубика Рубика
Совокупность математических методов для изучения свойств кубика Рубика Ромб. Решение 6 задачи
Ромб. Решение 6 задачи Теорема Пифагора. Урок 27
Теорема Пифагора. Урок 27 Функции нескольких переменных. Предел и непрерывность
Функции нескольких переменных. Предел и непрерывность Прямоугольные треугольники
Прямоугольные треугольники Сложение и вычитание десятичных дробей. Электронный урок
Сложение и вычитание десятичных дробей. Электронный урок Porządki kompozycji symetria i asymetria
Porządki kompozycji symetria i asymetria Предел функции
Предел функции Теория вероятности
Теория вероятности Сравнение дробей
Сравнение дробей Устный счет. Назови следующее число
Устный счет. Назови следующее число Метод интервалов
Метод интервалов