Содержание
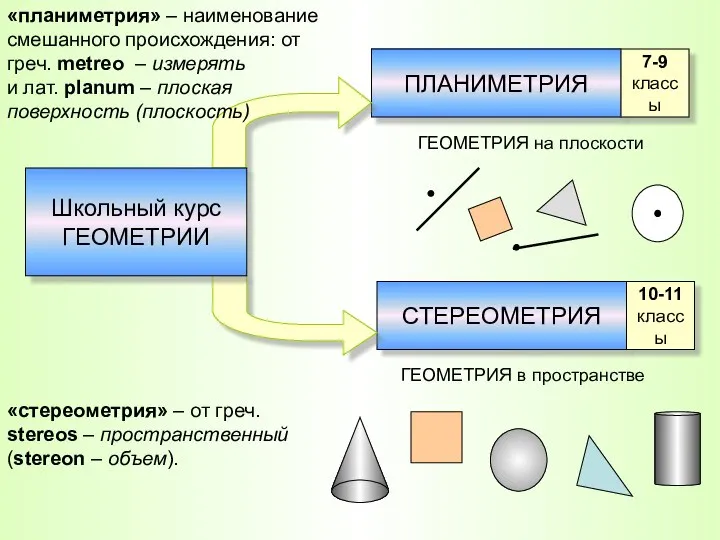
- 2. Школьный курс геометрии состоит из двух частей: ПЛАНИМЕТРИИ СТЕРЕОМЕТРИИ
- 3. ПЛАНИМЕТРИЯ СТЕРЕОМЕТРИЯ 7-9 классы 10-11 классы ГЕОМЕТРИЯ на плоскости ГЕОМЕТРИЯ в пространстве «планиметрия» – наименование смешанного
- 4. Планиметрия Стереометрия Изучает свойства геометрических фигур на плоскости Изучает свойства фигур в пространстве В переводе с
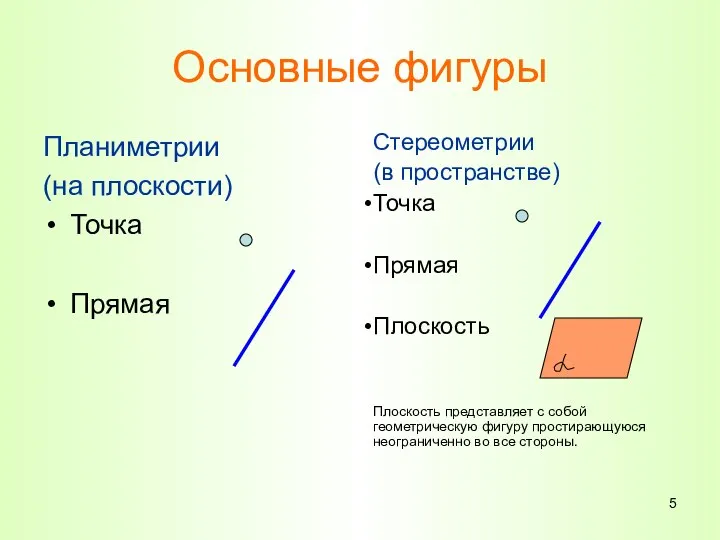
- 5. Основные фигуры Планиметрии (на плоскости) Точка Прямая Стереометрии (в пространстве) Точка Прямая Плоскость Плоскость представляет с
- 6. Наряду с точками, прямыми, плоскостями в стереометрии рассматриваются геометрические тела, изучаются их свойства, вычисляются площади их
- 7. ГЕОМЕТРИЯ возникла из практических задач людей; ГЕОМЕТРИЯ лежит в основе всей техники и большинства изобретений человечества;
- 8. Стереометрия широко используется в строительном деле, архитектуре, машиностроении, геодезии, во многих других областях науки и техники.
- 9. Оперный театр в Сиднее Датский архитектор Йорн Утцон был вдохновлён видом парусов.
- 10. Эйфелева башня Париж, Марсово поле Инженер Гюстав Эйфель нашел необычную форму для своего проекта. Эйфелева башня
- 11. Интуитивное, живое пространственное воображение в сочетании со строгой логикой мышления — это ключ к изучению стереометрии
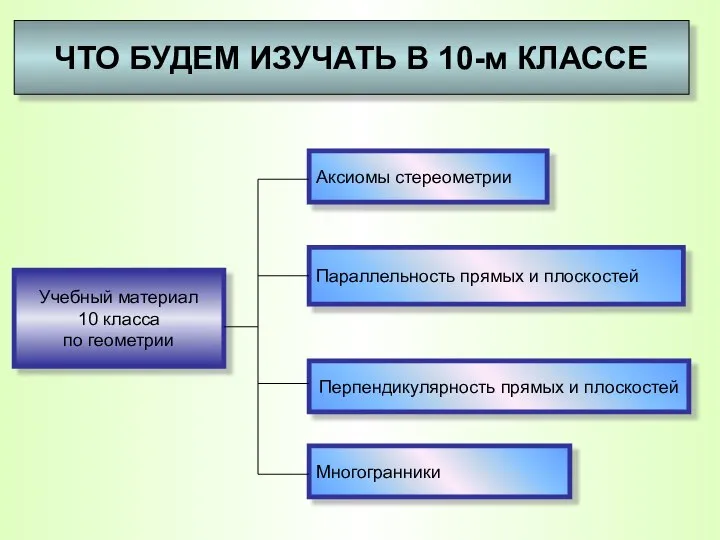
- 12. Учебный материал 10 класса по геометрии ЧТО БУДЕМ ИЗУЧАТЬ В 10-м КЛАССЕ
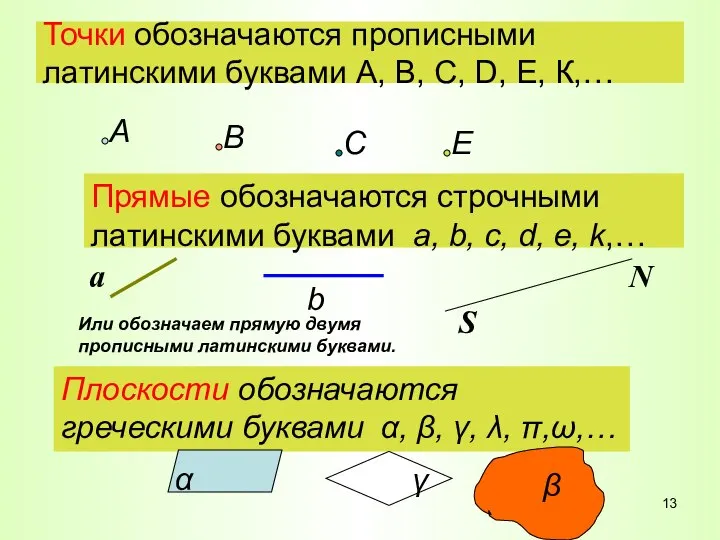
- 13. Точки обозначаются прописными латинскими буквами А, В, С, D, Е, К,… Прямые обозначаются строчными латинскими буквами
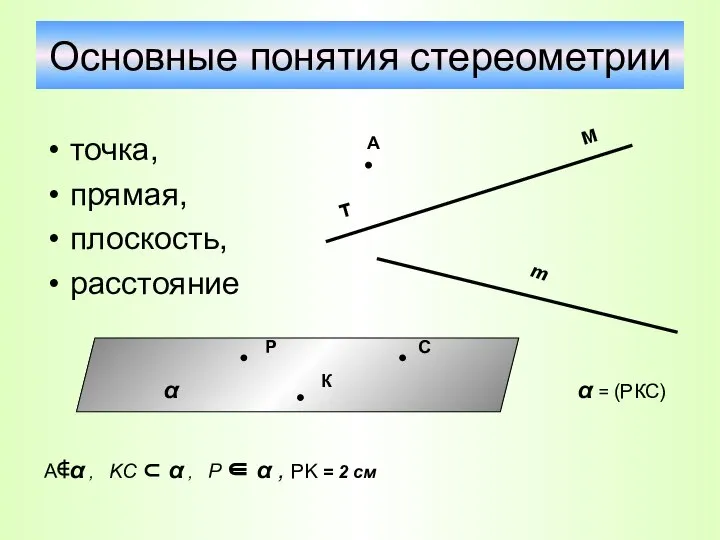
- 14. Основные понятия стереометрии точка, прямая, плоскость, расстояние α = (РКС) A∉α , KC ⊂ α ,
- 15. Аксиомы стереометрии Слово «аксиома» греческого происхождения и в переводе означает истинное, исходное положение теории. Основные свойства
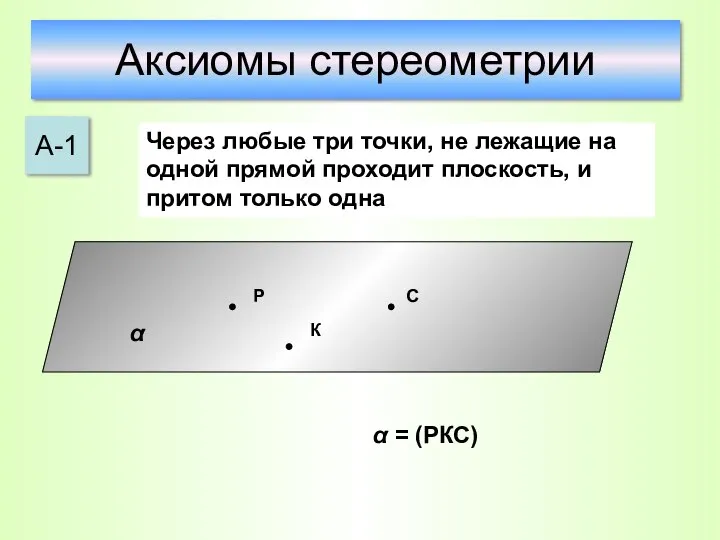
- 16. Аксиомы стереометрии А-1 Через любые три точки, не лежащие на одной прямой проходит плоскость, и притом
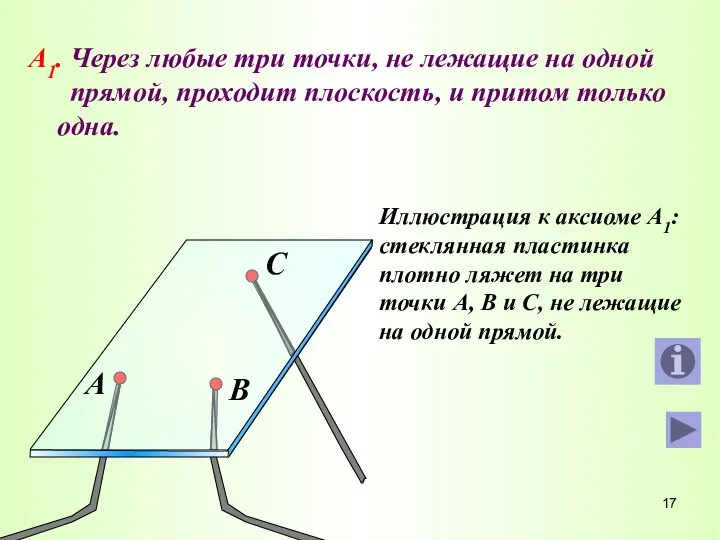
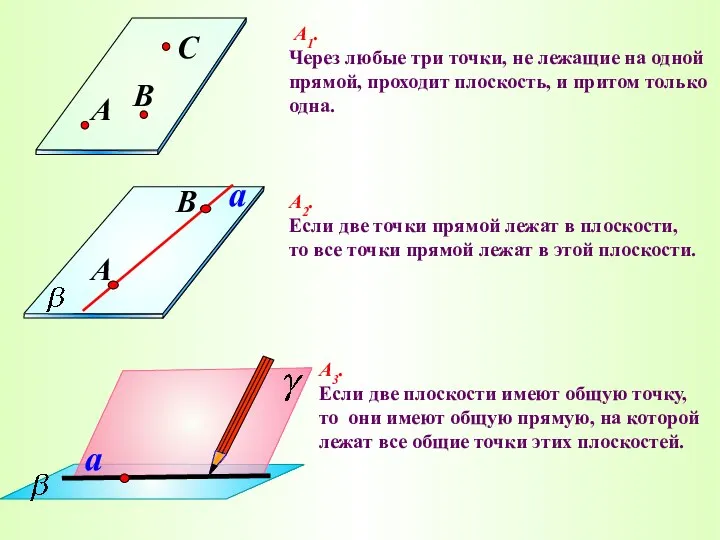
- 17. А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
- 18. Иллюстрации к аксиоме А1 из жизни. Табурет с тремя ножками всегда идеально встанет на пол и
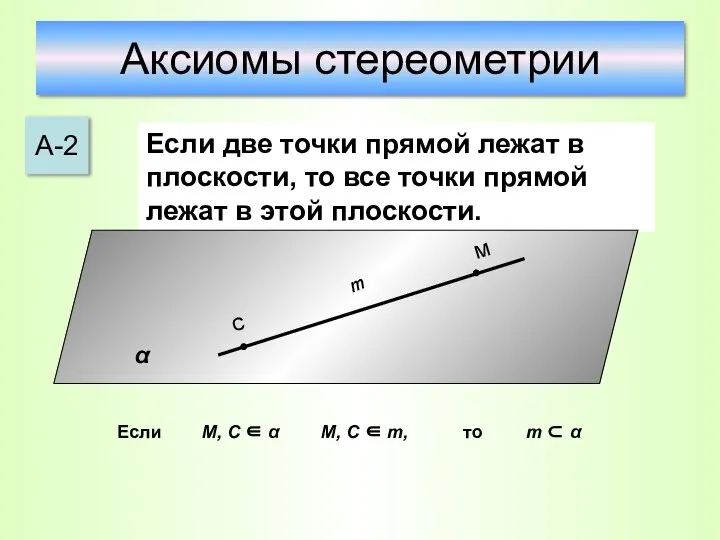
- 19. Аксиомы стереометрии А-2 Если две точки прямой лежат в плоскости, то все точки прямой лежат в
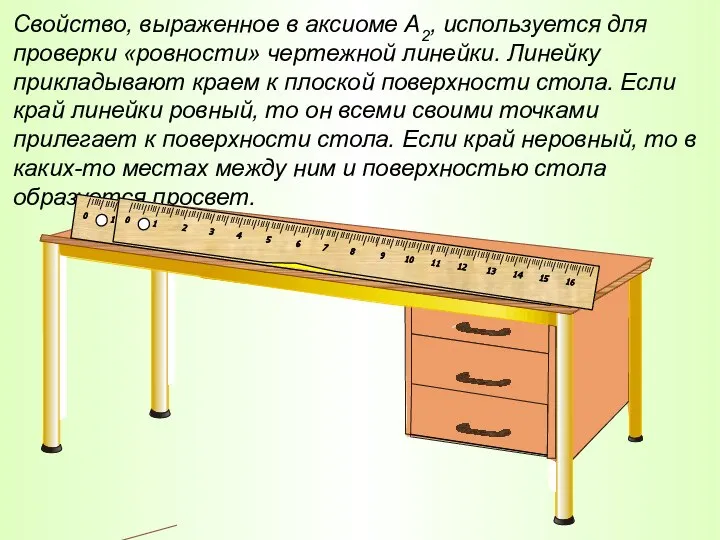
- 20. Свойство, выраженное в аксиоме А2, используется для проверки «ровности» чертежной линейки. Линейку прикладывают краем к плоской
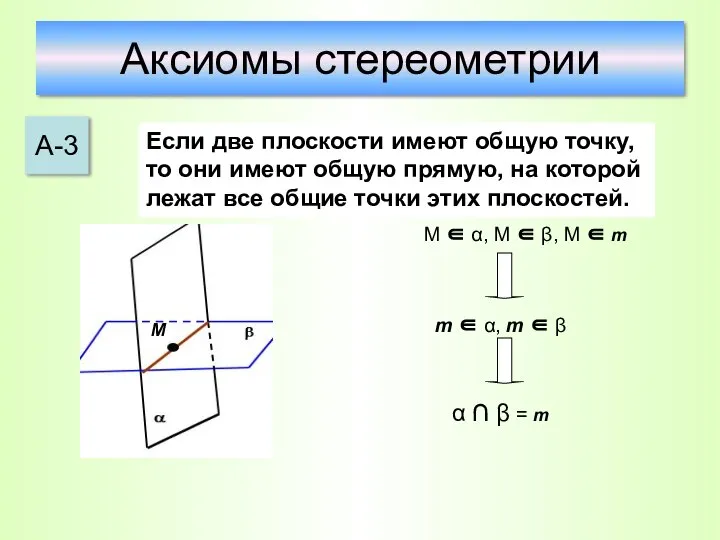
- 21. Аксиомы стереометрии А-3 Если две плоскости имеют общую точку, то они имеют общую прямую, на которой
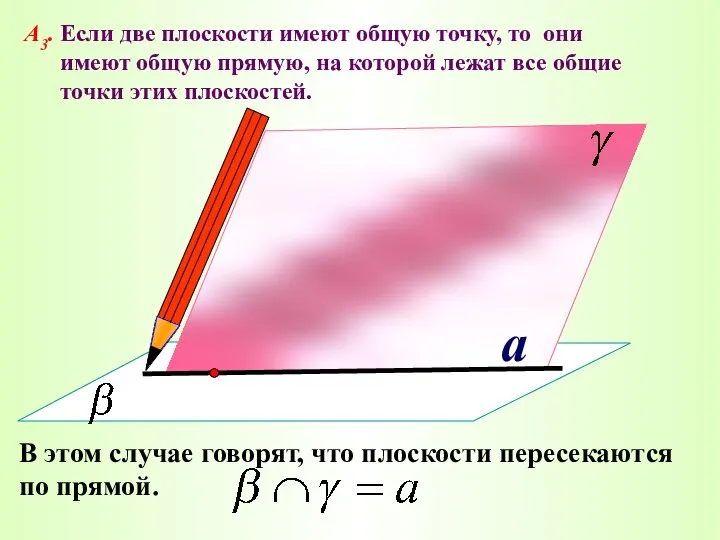
- 22. a А3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат
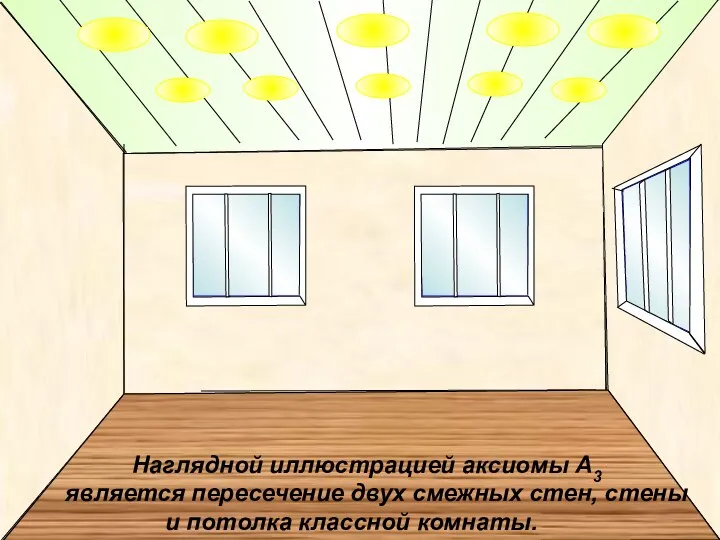
- 23. Наглядной иллюстрацией аксиомы А3 является пересечение двух смежных стен, стены и потолка классной комнаты.
- 24. А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
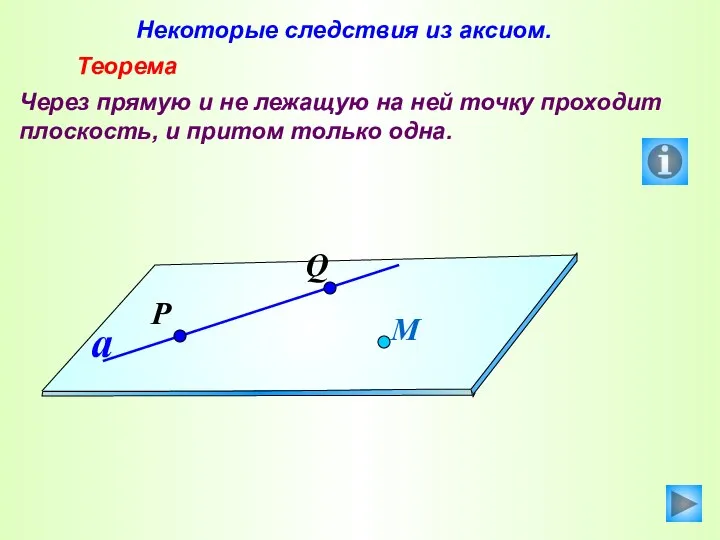
- 25. Некоторые следствия из аксиом. Теорема Через прямую и не лежащую на ней точку проходит плоскость, и
- 26. СЛЕДСТВИЯ ИЗ АКСИОМ Т-1 Через любую прямую и не принадлежащую ей точку можно провести плоскость, и
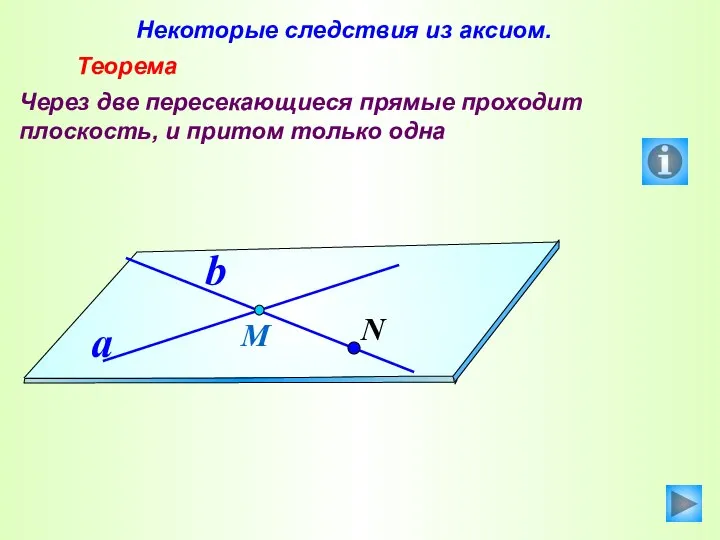
- 27. Некоторые следствия из аксиом. Теорема Через две пересекающиеся прямые проходит плоскость, и притом только одна М
- 28. СЛЕДСТВИЯ ИЗ АКСИОМ Т-2 Через любые две пересекающиеся прямые можно провести плоскость, и притом только одну.
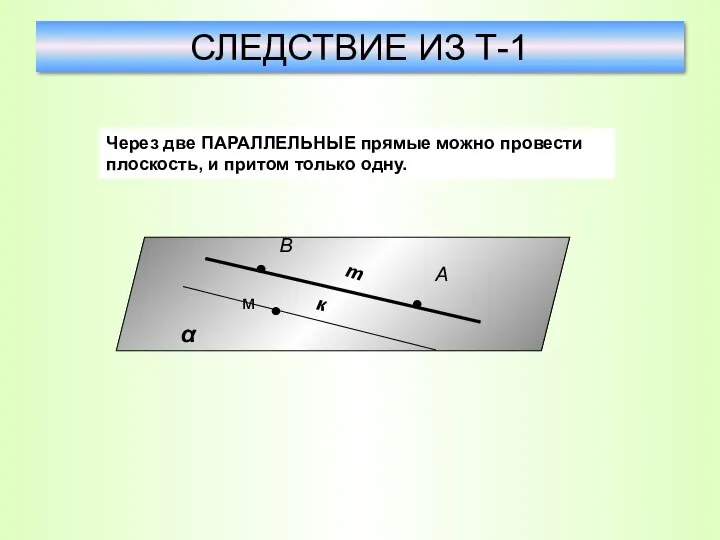
- 29. СЛЕДСТВИЕ ИЗ Т-1 Через две ПАРАЛЛЕЛЬНЫЕ прямые можно провести плоскость, и притом только одну. к
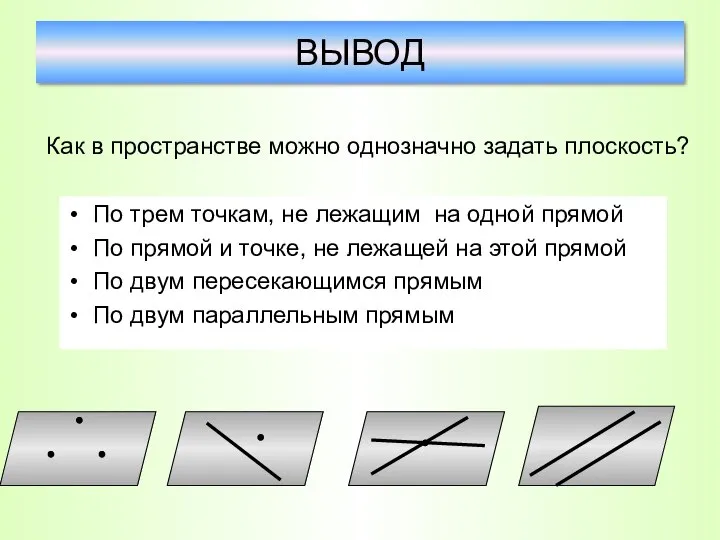
- 30. По трем точкам, не лежащим на одной прямой По прямой и точке, не лежащей на этой
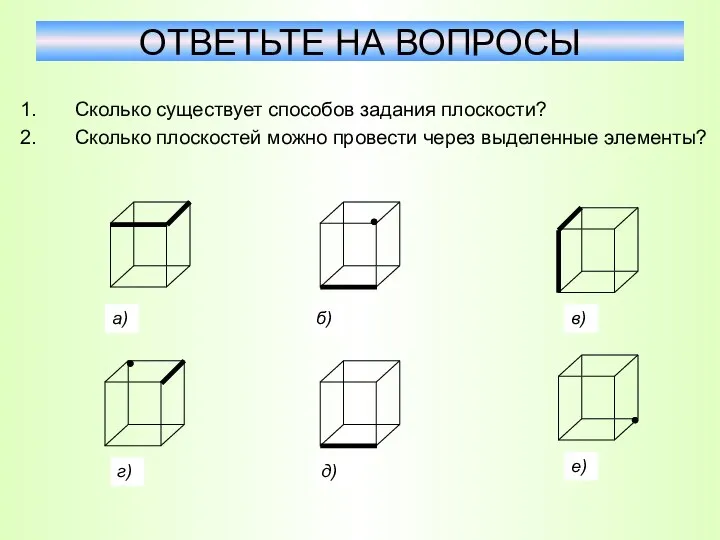
- 31. Сколько существует способов задания плоскости? Сколько плоскостей можно провести через выделенные элементы? ОТВЕТЬТЕ НА ВОПРОСЫ а)
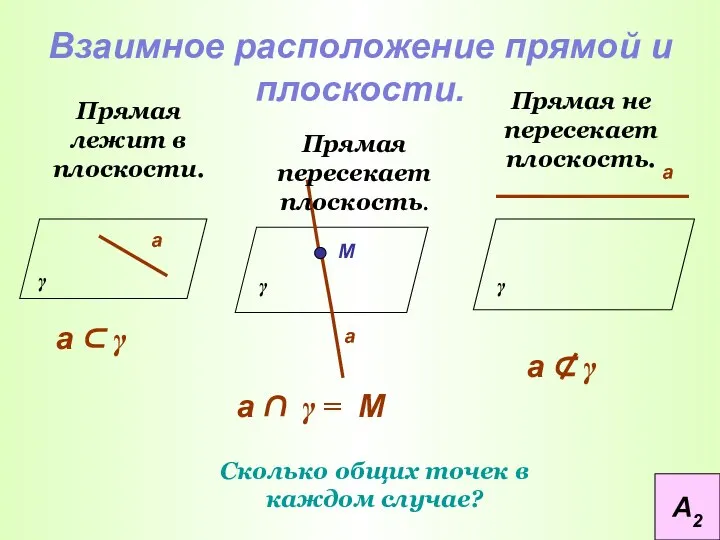
- 32. Взаимное расположение прямой и плоскости. Прямая лежит в плоскости. Прямая не пересекает плоскость. Сколько общих точек
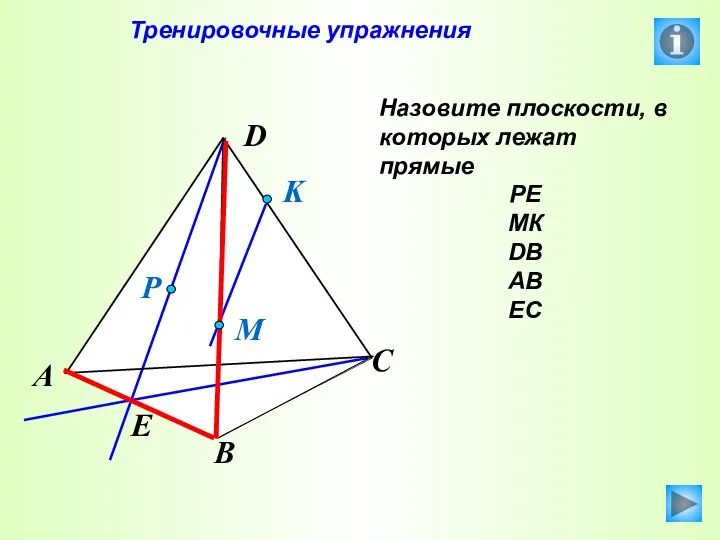
- 33. Тренировочные упражнения Назовите плоскости, в которых лежат прямые РЕ МК DB AB EC P E A
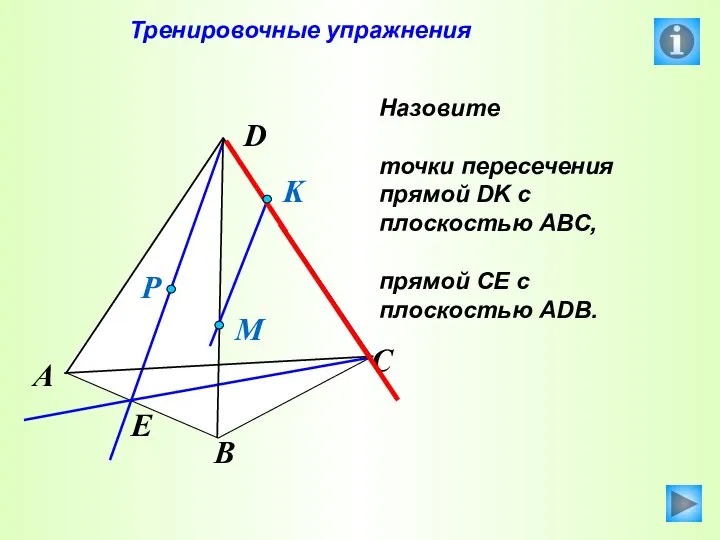
- 34. Тренировочные упражнения Назовите точки пересечения прямой DK с плоскостью АВС, прямой СЕ с плоскостью АDB. P
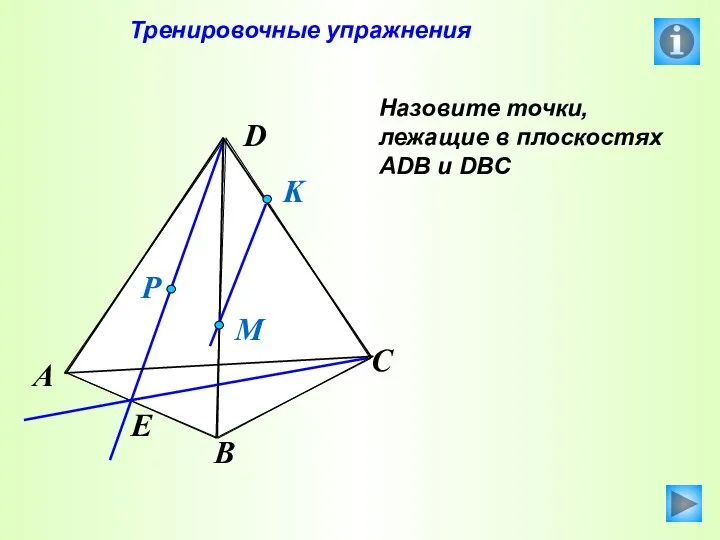
- 35. Тренировочные упражнения Назовите точки, лежащие в плоскостях АDB и DBC P E A B C D
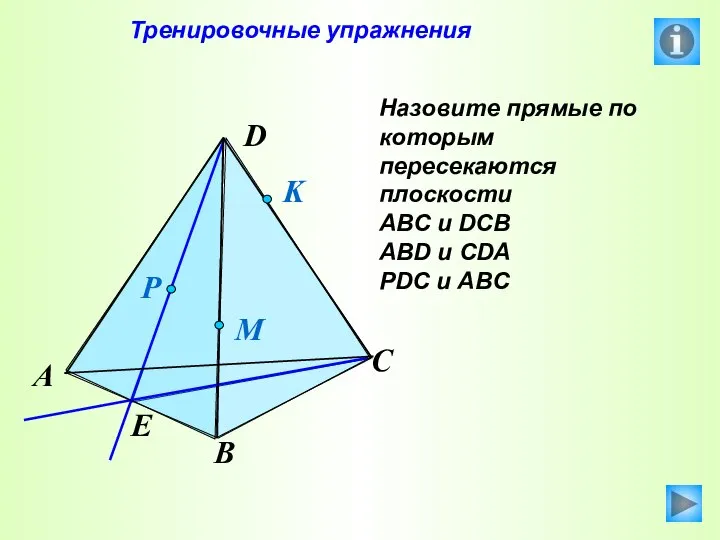
- 36. Тренировочные упражнения Назовите прямые по которым пересекаются плоскости АВС и DCB ABD и CDA PDC и
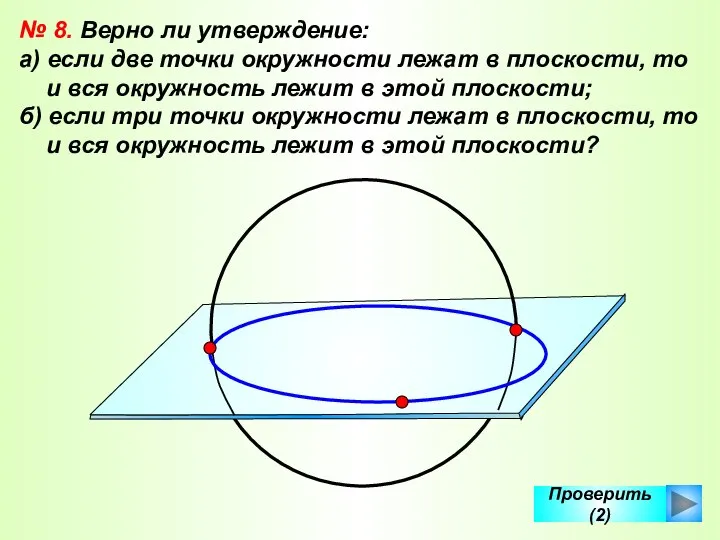
- 37. Проверить (2) № 8. Верно ли утверждение: а) если две точки окружности лежат в плоскости, то
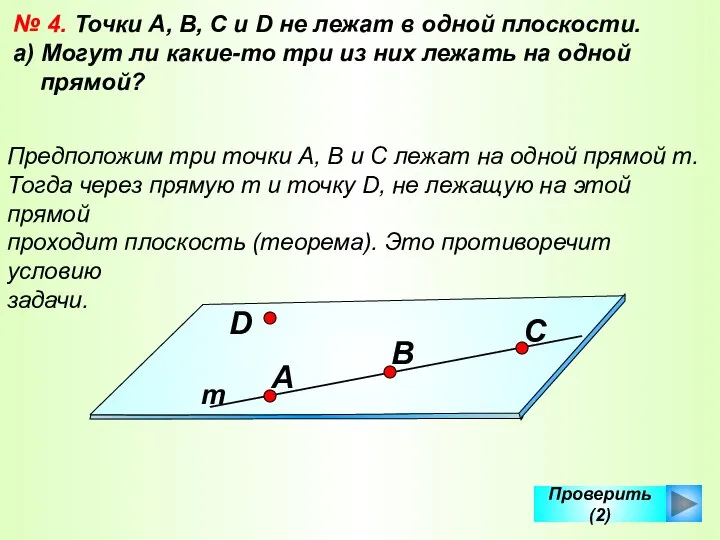
- 38. Проверить (2) № 4. Точки А, В, С и D не лежат в одной плоскости. а)
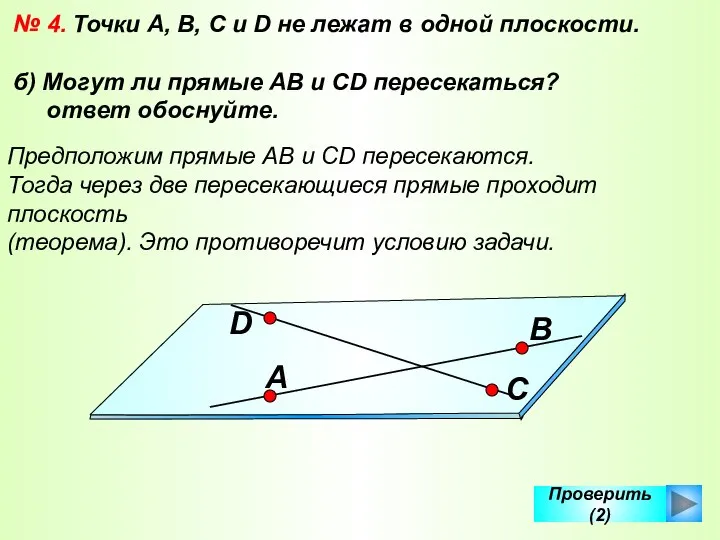
- 39. Проверить (2) № 4. Точки А, В, С и D не лежат в одной плоскости. б)
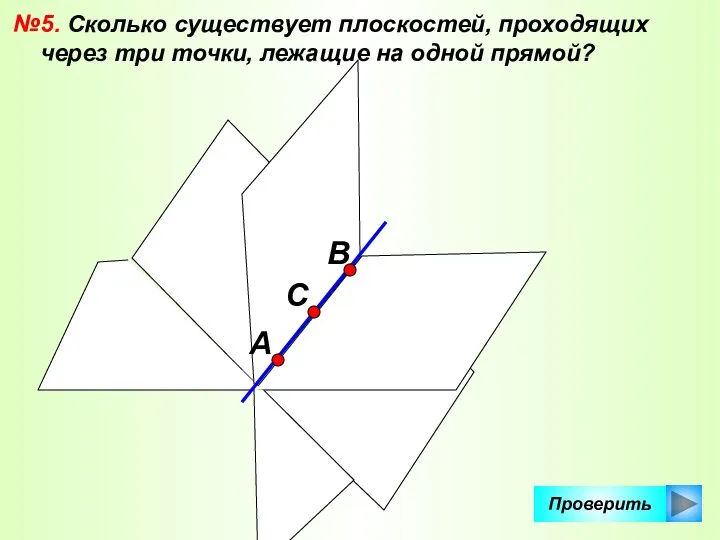
- 40. Проверить №5. Сколько существует плоскостей, проходящих через три точки, лежащие на одной прямой? А С В
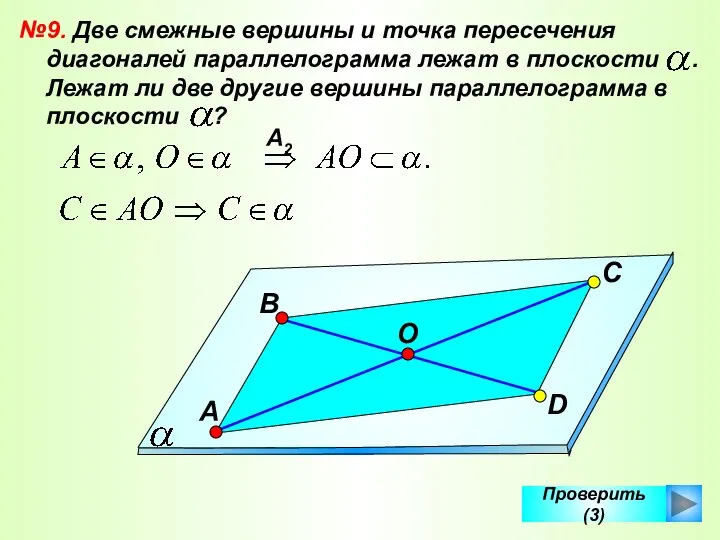
- 41. Проверить (3) №9. Две смежные вершины и точка пересечения диагоналей параллелограмма лежат в плоскости . Лежат
- 43. Скачать презентацию












 Памятка по оформлению краткой записи к задачам
Памятка по оформлению краткой записи к задачам Ребус Буквы
Ребус Буквы Решение задач по теме: Показательная, степенная и логарифмическая функции
Решение задач по теме: Показательная, степенная и логарифмическая функции Нахождение числа по его дроби
Нахождение числа по его дроби СРС 2 ВСК 2. Задачи
СРС 2 ВСК 2. Задачи Зимующие птицы
Зимующие птицы Доверительные интервалы
Доверительные интервалы Презентация на тему Второй признак равенства треугольников 7 класс
Презентация на тему Второй признак равенства треугольников 7 класс  Решение задач Асимптота
Решение задач Асимптота Абсолютная и относительная погрешность округления чисел
Абсолютная и относительная погрешность округления чисел Решение задач на множества
Решение задач на множества Тела вращения. Конус
Тела вращения. Конус Задачи на проценты
Задачи на проценты Распределительное свойство умножения. Упрощение выражений
Распределительное свойство умножения. Упрощение выражений Системы распознавания образов
Системы распознавания образов Презентация на тему Связь между суммой и слагаемыми (1 класс)
Презентация на тему Связь между суммой и слагаемыми (1 класс)  Логарифмические неравенства
Логарифмические неравенства Прикладной количественный анализ заголовков
Прикладной количественный анализ заголовков Диаграммы
Диаграммы Части задачи
Части задачи Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Страна Математика
Страна Математика Решение задач на одновременное встречное движение
Решение задач на одновременное встречное движение Квадратный корень из степени
Квадратный корень из степени Побудова математичних моделей. Заняття №2
Побудова математичних моделей. Заняття №2 Презентация по математике "Отношение больше, меньше" -
Презентация по математике "Отношение больше, меньше" -  Сложение и вычитание чисел с разными знаками
Сложение и вычитание чисел с разными знаками Предел числовой последовательности и его свойства
Предел числовой последовательности и его свойства