Содержание
- 2. Зарождение динамики неголономных систем, по-видимому, следует отнести к тому времени, когда аналитический формализм, созданный трудами Л.
- 3. Только в 1894 г. в книге «Принципы механики, изложенные в новой связи» (через 106 лет после
- 4. Достаточно полное изложение задач и методов неголономной механики представлено в монографии Ю.И.Неймарка, Н.А.Фуфаева "Динамика неголономных систем"
- 5. Условия голономные и неголономные. Условия (они же ограничения), накладываемые на движение механической системы разделяют как потенциальные:
- 6. Условия голономные и неголономные. Задача учета кинематических связей в нелинейном виде не существует физически или, в
- 7. Условия голономные и неголономные. Если дифференциальную связь (3) нельзя записать как полный дифференциал некоторой функции, не
- 8. Условия голономные и неголономные. (2) а1 [ х,у ] х + а2 [х,у ] у =0
- 9. Методы составления уравнений динамики механической системы при наложении различных типов условий на переменные. (2) а1 [
- 10. Методы составления уравнений динамики механической системы при наложении различных типов условий на переменные. (2) а1 [
- 11. НОВЫЙ МЕТОД (2) а1 [ х,у ] х + а2 [х,у ] у =0 1) Эквивалентен
- 12. (2) а1 [ х,у ] х + а2 [х,у ] у =0 Однако, способ уменьшения числа
- 13. Указанное выражение получается совершенно естественно при вычислении вариации интеграла действия Гамильтона; в современных обозначениях: dΩ =d[x1]⋀d[x]-d[H]⋀d[t]
- 14. НОВЫЙ МЕТОД Поскольку из этого дифференциального инварианта следует система уравнений движения - любой механической системы, а
- 15. В этом случае использование интегрального инварианта механике по Картану, введение ограничений на переменные механической системы (как
- 16. Применение нового метода к составлению уравнений механических движения волнового твердотельного гироскопа ( по В.Ф. Журавлеву, Д.М.
- 17. L=1/2 ((v1+(R-w) Ω)2+(w1+v Ω)2)- 1/2 κ12 (wss+vs )2- -(1/2 ) δ12 (vs -w)2 условие нерастяжимости средней
- 18. применение нового метода дало основные соотношения: d°SID°us-1/Ω2 (-(1/2)d[Ω2 rψ2+Ω2 vψ2]+((R+r)2+v2) d[Ω2/2])⋀d[ψ])⋀d[φ] 1/Ω2 (1/2 d[Ω2 rψ2+Ω2 vψ2]-((R+r)2+v2)
- 19. В рамках приближений введеных авторами книги (применение к полученным уравнениям упрощение v/ -w->0(линеаризация) условия нерастяжимости средней
- 20. однако у Вас при выводе уравнений динамики кольца учитывается только первое соотношение : v/-w=0 второе соотношение
- 21. интересно сравнить с: vs+R-w-> R Cos[Q],-ws-v-> R Sin[Q] получается, что при малом Q,данные соотношения зависят от
- 22. Эффект инертных свойств упругой деформацией гибкого кольца следует из уравнений кольца и в случае когда потенциальной
- 23. Уравнение динамики для переменных гибкого кольца эквивалентно : 1/2 d[Ω2 rψ2+Ω2 vψ2]-((R+r)2+v2) d[Ω2/2]=0 ((R+r)2+v2) d[Ω2/2]=1/2 d[r12+v12]
- 25. Скачать презентацию





![Условия голономные и неголономные. (2) а1 [ х,у ] х + а2](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/892484/slide-7.jpg)


![НОВЫЙ МЕТОД (2) а1 [ х,у ] х + а2 [х,у ]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/892484/slide-10.jpg)
![(2) а1 [ х,у ] х + а2 [х,у ] у =0](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/892484/slide-11.jpg)





![применение нового метода дало основные соотношения: d°SID°us-1/Ω2 (-(1/2)d[Ω2 rψ2+Ω2 vψ2]+((R+r)2+v2) d[Ω2/2])⋀d[ψ])⋀d[φ] 1/Ω2](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/892484/slide-17.jpg)


![интересно сравнить с: vs+R-w-> R Cos[Q],-ws-v-> R Sin[Q] получается, что при малом](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/892484/slide-20.jpg)

![Уравнение динамики для переменных гибкого кольца эквивалентно : 1/2 d[Ω2 rψ2+Ω2 vψ2]-((R+r)2+v2)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/892484/slide-22.jpg)
 Модуль числа (часть 2)
Модуль числа (часть 2) Второй признак равенства треугольников по стороне и двум прилежащим к ней углам
Второй признак равенства треугольников по стороне и двум прилежащим к ней углам Пространственные и временные представления
Пространственные и временные представления Построение графика квадратичной функции
Построение графика квадратичной функции Методика проверки и оценки алгебраических заданий повышенного уровня сложности
Методика проверки и оценки алгебраических заданий повышенного уровня сложности Теория погрешностей
Теория погрешностей Презентация на тему Задачи на движение для учителя
Презентация на тему Задачи на движение для учителя  Презентация на тему Устный счет по математике
Презентация на тему Устный счет по математике  Пирамиды
Пирамиды Презентация по математике "Что такое понятие" -
Презентация по математике "Что такое понятие" -  Дискретная математика
Дискретная математика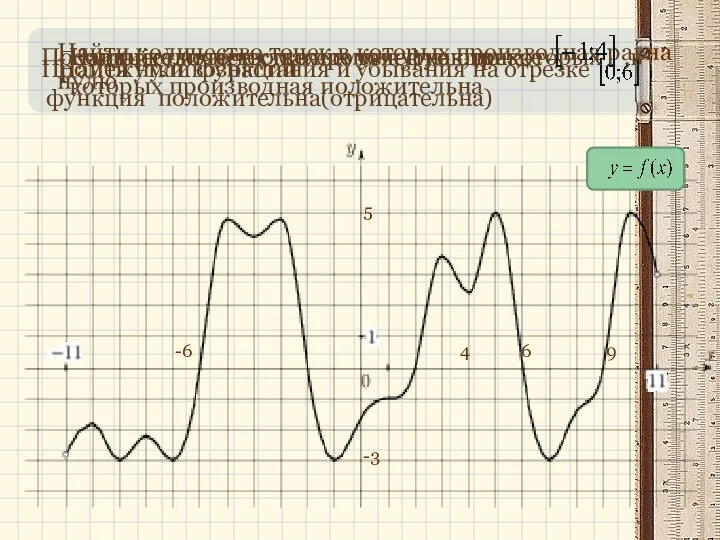 Алгоритм нахождения интервалов выпуклости и точек перегиба
Алгоритм нахождения интервалов выпуклости и точек перегиба Свойства функции
Свойства функции Определение производной. Физический смысл производной
Определение производной. Физический смысл производной Графический диктант Раскрытие скобок
Графический диктант Раскрытие скобок Презентация на тему Подготовка к контрольной работе по алгебре
Презентация на тему Подготовка к контрольной работе по алгебре  Произведение вектора на число
Произведение вектора на число Длина окружности. Площадь круга
Длина окружности. Площадь круга Свойства параллельных прямых. Решение задач
Свойства параллельных прямых. Решение задач Элементы комбинаторики
Элементы комбинаторики Умножение десятичной дроби на десятичную дробь
Умножение десятичной дроби на десятичную дробь Математическая модель
Математическая модель Периодичность синуса и косинуса y = sin x; у = cos x
Периодичность синуса и косинуса y = sin x; у = cos x Регулятивные удд
Регулятивные удд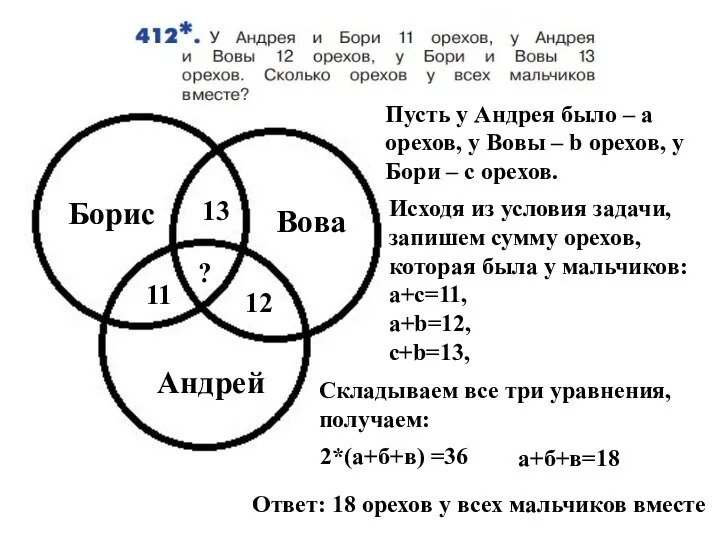 Уравнения. Задача
Уравнения. Задача Выборочное наблюдение. Практическое занятие
Выборочное наблюдение. Практическое занятие Законы умножения для обыкновенных дробей. 5 класс
Законы умножения для обыкновенных дробей. 5 класс Сумма углов треугольника. Виды треугольников
Сумма углов треугольника. Виды треугольников